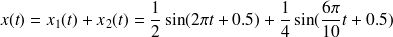Mélange de fréquences. Notion de spectres
Nous avons vu qu'une fréquence était associée à une fonction sinusoïdale., Nous allons voir que l'on peut mélanger des fréquences et qu'il faut alors additionner des fonctions sinus.
Exemple : Mélange de deux sinus
Soient les deux fonctions sinusoïdales suivantes :
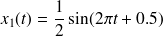en bleu.
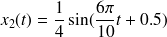en vert.
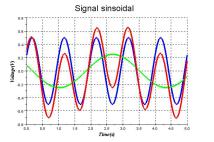 Mélange de deux sinus | La fonction tracée en rouge est un mélange de deux fréquences. Son expression mathématique est :
|
Exemple : Clavier de téléphone
Numérotation DTMF (Dual-Tone Multi-Frequency)
Lorsque vous composez un numéro de téléphone, vous effectuez sans le savoir un mélange de deux fréquences.
 Clavier de téléphone | Appui sur 0 1336Hz + 941Hz Appui sur 9 1633Hz + 852Hz |
Exemple :
Voici ce que vous pouvez entendre si vous composez le numéro de téléphone du secrétariat de MP. Sur une ligne fixe, si vous faites écouter ce signal il y a des chances que cela sonne en MP !
Fondamental : Notion de spectre
Pour représenter un signal nous avons maintenant deux possibilités, la représentation temporelle que vous connaissez déjà et et le spectre en fréquence du signal.
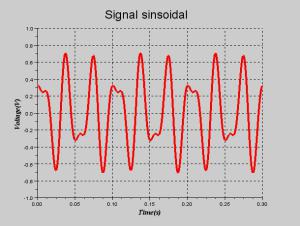
 Mélange de 30Hz et 50Hz | Représentation temporelle d'un mélange de deux fréquences 30 et 50hz |
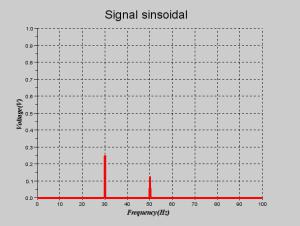
Spectre : Représentation fréquentielle d'un mélange de deux fréquences 30 et 50hz |  Mélange de 30Hz et 50Hz |
Vous pouvez essayer de mélanger 3 sinus en fixant les amplitudes et les fréquences de chaque composante. Vous pourrez voir et écouter le résultat.
