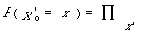
1 . Introduction

Dans le cadre du projet Applications Multimodales pour Interfaces et Bornes Evoluées ( projet AMIBE soutenu par les PRC Informatique 1993 - 1995 ), est étudiée la bi-modalité naturelle auditive et visuelle de la communication orale. La reconnaissance automatique de la parole s'opère en synchronisant une "lecture labiale" avec un module de reconnaissance des formes acoustiques, par Modèles de Markov Cachés (MMC).

Pour fusionner les données acoustiques et articulatoires, plusieurs alternatives se présentent. Les informations peuvent être traitées sans discernement, par un MMC classique ; le vecteur d'observations est la concaténation des deux familles de paramètres labiaux et acoustiques ; ils sont considérés comme indépendants et l'utilisation de pondérations permet de réduire l'importance de l'une par rapport l'autre ( nous parlerons, dans la suite de cet article d'approche globale et de MMC global ). Une deuxième alternative consiste à modéliser chaque famille de paramètres par un modèle de type MMC, et corréler les deux modèles par une dépendance entre les lois. Nous avons étudié plus particulièrement cette approche appelée par la suite approche maître-esclave ; nous nous sommes inspirés des travaux de Brugnara et De Mori qui ont appliqué cette liaison maître-esclave pour traiter la durée des sons [Brugnara, 92].

Au cours de cette présentation, le principe de l'approche maître-esclave est rappelé brièvement, et nous définissons un MMC équivalent moyennant certaines hypothèses simplificatrices appropriées à la reconnaissance de paramètres acoustiques et labiaux. Des résultats expérimentaux illustrent cette approche, dans les cas de la reconnaissance de suites de chiffres et lettres épelées. Une comparaison entre approche globale et approche maître-esclave est proposée.

2 . Principe du modèle théorique :

Le principe des modèles dits "maître-esclave" repose sur la modélisation d'une application non plus par un MMC unique, mais par deux MMC mis en parallèle et corrélés. L'idée générale est de parvenir à une adaptation dynamique des lois de probabilités d'un des modèles de Markov cachés, en fonction du contexte courant modélisé par l'autre MMC. Le contexte est une notion qui doit être prise au sens large, il peut s'agir d'un indice de voisement, de nasalisation,... d'un réel contexte phonétique, d'un indice suprasegmental comme la durée des sons... tandis que le MMC piloté est traditionnellement lié à des paramètres acoustiques.

Un modèle maître-esclave se compose de deux modèles, un modèle maître [[lambda]]' et un modèle esclave [[lambda]]'', définis comme suit :

-- Le modèle [[lambda]]' est un MMC classique, composé de deux processus stochastiques X', Y' :

* le processus caché X' est à valeurs dans [[chi]]' = {x'} ensemble d'états fini et vérifie :

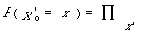
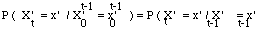
= a' z'x' avec x' t-1 = z'.

* le processus Y' est à valeurs dans un ensemble mesurable V' et vérifie :

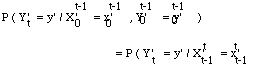
= b' z'x' (y').

-- Le modèle [[lambda]]^" est un MMC dont les paramètres dépendent à tout instant de l'état dans lequel se trouve le modèle maître :

* le processus caché X" est à valeurs dans [[chi]]" = { x"} ensemble d'états fini de la manière suivante :

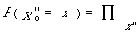
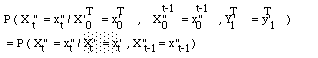= a" z"x"x'

avec x" t-1 = z" et x' t = x'.

* le processus Y" est à valeurs dans un ensemble mesurable V" et vérifie :

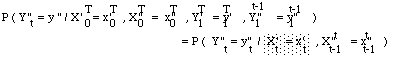= b" z"x"x' (y").

Le modèle maître-esclave [[lambda]] = ( [[lambda]]', [[lambda]]") est décrit par l'ensemble des paramètres

( [[Pi]]', [[Pi]]", a'.., b'... (.), a".., b"... (.) )

La vraisemblance d'une suite d'observations y1^T = ( y'1^T, y"1^T) par rapport au modèle [[lambda]] = ( [[lambda]]', [[lambda]]") est donnée par :

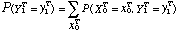
qui s'écrit, après application de la règle de Bayes, à l'aide des deux expressions suivantes :

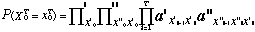
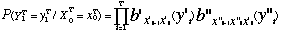
Etant donné une suite d'observations y1^T = ( y'1^T, y"1^T), la recherche du chemin le plus probable ayant généré cette séquence s'obtient par un algorithme de Viterbi modifié :

si

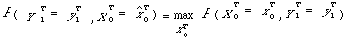on introduit la variable:

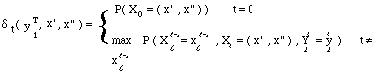qui se calcule par récurrence

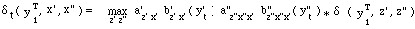
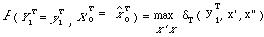
3 . Modèle équivalent:

Un modèle maître-esclave est équivalent mathématiquement à un modèle classique de type MMC. En reprenant les notations du paragraphe précédent, le processus caché X est alors un double processus (X', X") à valeurs dans le produit cartésien [[chi]]'x [[chi]]" de cardinal N' ^x N" :

un état de X est caractérisé par le couple d'états x=( x',x"),

Le processus observable Y = ( Y' , Y" ) est à valeurs dans l'ensemble mesurable V'x V" :

une observation de Y est caractérisée par le couple d'observations y = (y',y")

Les N' N" probabilités initiales et les (N' N")² probabilités de transitions et lois d'observations du modèle de Markov caché [[lambda]] = ( X , Y ) sont caractérisées par les contraintes :

a xz = a'x'z' a"x"z"z'

bxz(y) = b' x'z'(y') b"x"z"z'(y")

[[Pi]] x = [[Pi]]' x' [[Pi]]"x"x'

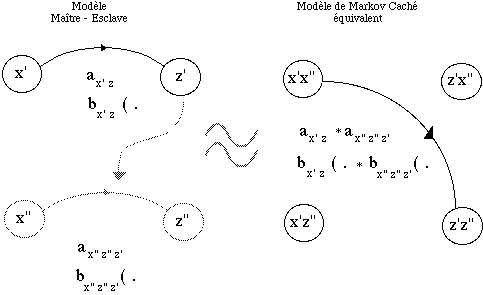
Figure 1 : Modèle maître-esclave et son modèle équivalent

L'inconvénient de ce modèle réside dans son important nombre d'états et de lois (figure 1). Ne pouvant raisonnablement implanté un tel modèle, nous avons émis des hypothèses simplicatrices.

Hypothèses simplificatrices

Dans le cadre de notre application, le modèle maître décrit le contexte labial. Nous supposons que toute configuration est équiprobable indépendamment de la précédente, ce qui s'exprime par :

-- tout état est équiprobable et en particulier

a'x'z' = 1 / N, si N est le nombre d'états.

-- les lois d'observations portées par les transitions ( x'z' ) ne dépendent que de l'état d'arrivée z'

b' x'z'(y') = b' t'z'(y') pour tout t',x',y'.

Il s'en suit que l'on peut remplacer le modèle équivalent par un modèle simplifié dont le nombre d'états est le nombre d'états du modèle esclave, mais chaque transition du modèle esclave est dupliquée par le nombre d'états du modèle maître et chaque nouvelle transition est indexée par un état maître (figure 2).

Mise en oeuvre

Nous avons créé le modèle simplifié présenté ci dessus à l'aide d'un compilateur de MMC [Jacob 94]. Un premier réseau est construit et correspond à celui du modèle esclave, le nombre de transitions non vides entre chaque couple d'états est multiplié par le nombre d'états du modèle maître, ainsi que le nombre de lois d'observations ; à chacune de ces nouvelles transitions et lois est attribué un numéro d'état maître. Le nombre de coefficients par vecteur d'observations correspondant respectivement à l'observation maître ( y' ) et à l'observation esclave (y") est indiqué lors de l'apprentissage, l'algorithme est modifié de façon à effectuer les réestimations selon les contraintes du modèle équivalent. Le programme de reconnaissance est classique.

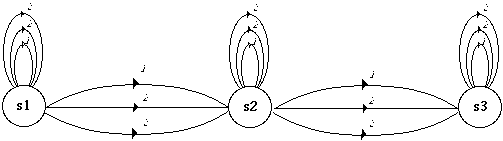
Figure 2 : Représentation du réseau maître-esclave simplifié correpondant à un modèle maître de 3 états. Les transitions supportant une loi d'observation sont dupliquées en trois. Chaque duplicata de la loi porte un numéro d'état maître et les transitions de probabilité sont mises à jour.

4 . Expérimentations :

Dans le cadre du projet AMIBE, nous disposons de deux types de signaux : le signal acoustique et le signal articulatoire synchronisé. Le signal acoustique est échantillonné à 16 kHz, tandis que pour le signal articulatoire (issu d'un traitement d'image [Lallouache 91]), nous disposons d'un vecteur d'observations toutes les 20ms. Ce signal se compose de la largeur A et la hauteur B internes du contour des lèvres, et la surface intérolabiale S (figure 3).

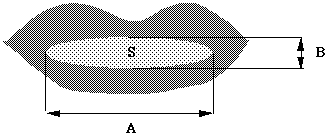
Figure 3 : Coefficients labiaux.

Pré-traitement des données :

Le signal acoustique est segmenté automatiquement [André-Obrecht, 88] et une analyse spectrale est faite sur chaque segment : 8 coefficients cepstraux ( MFCC ) sont obtenus après recalage du spectre selon l'échelle Mel. Leur sont adjoints l'énergie (E) et la dérivée de ces coefficients ( [[Delta]] MFCC, [[Delta]] E ). Les frontières issues de la segmentation statistique sont projetées sur les signaux articulatoires. Pour chaque segment projeté, est calculée une valeur moyenne de chaque paramètre labial ainsi que les dérivées correspondantes .

Le vecteur d'observations est finalement composé de 18 coefficients de nature acoustique, de 6 coefficients articulatoires, auxquels est ajoutée la longueur du segment correspondant ( T ).

Système de reconnaisance :

Pour fusionner les données acoustiques et articulatoires, nous avons envisagé un modèle équivalent simplifié correspondant au modèle maître-esclave suivant (figure 4):

-- le modèle Maître est un modèle ergodique à 3 états modélisant les configurations des lèvres : ouvertes , fermées et semi-ouvertes.

-- le modèle Esclave est un modèle gauche-droit modélisant le signal acoustique.

Les unités acoustiques sont des pseudo-diphones ; le modèle esclave est organisé sous forme de concaténation de modèles de mots, chaque modèle de mot est lui-même construit à partir des modèles de pseudo-diphones [André-Obrecht 93].

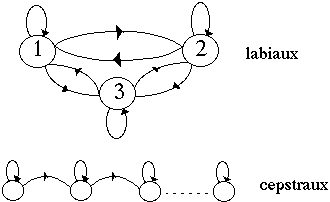
Figure 4: MMC Maître-Esclave du projet AMIBE

* Données :

Cette application de reconnaissance est monolocuteur et le système est évalué sur deux corpus de phrases :

-- Corpus des chiffres : chacune des phrases est composée de 4 chiffres connectés ou des mots "oui" ou "non". L'ensemble d'apprentissage est formé de 84 prononciations de phrases ( 288 mots de base ). L'ensemble de test est formé de 35 phrases ( soit 125 mots ). L'ensemble d'apprentissage n'est pas suffisant pour apprendre correctement un nombre élevé de paramètres. Nous n'avons donc pas utilisé les dérivées des coefficients dans cette première expérience.

-- Corpus des lettres : chacune des phrases est composée de 4 lettres épelées. L'ensemble d'apprentissage contient 158 phrases ( soit 632 mots ) et l'ensemble de test se compose de 48 phrases ( soit 192 mots ).

* Résultats :

Afin de valider ce type d'approche, nous avons comparé systématiquement les taux de reconnaissances à ceux obtenus à l'aide d'un modèle de Markov Caché global Mglob construit de manière classique ; chaque mot du langage est décrit à partir de la notion de pseudo-diphone, et chaque pseudo-diphone correspond à un MMC élémentaire. Un vecteur d'observations est traité globalement, à raison d'une loi gaussienne par transition ( matrice de covariance diagonale ).

R I / RéSULTATS SUR LE CORPUS DES CHIFFRES :

Pour l'application des chiffres connectés , un modèle global est appris avec 8 coefficients cepstraux, l'Energie du signal E, et la durée du Segment T. A celui-ci est adjoint les 3 coefficients labiaux dans un deuxième temps. Il est comparé au modèle Maître-Esclave dont les coefficients labiaux font partie des paramètres initiaux. Le nombre de chiffres à reconnaître est imposé, soit 4.

 modèle          coefficients         phrases  mots   
                                       / 35    / 125  
M glob     8 MFCC + E + T                1     1      
           8 MFCC + E + T + A + B +      3     3      
           S                                          
M m/e      8 MFCC + E + T + A + B +      5     5      
           S                                          

Les meilleurs résultats sont obtenus avec un MMC classique M glob avec 8 coefficients cepstraux (figure 5). Nous observons que le traitement segmental ne dégrade pas les performances de reconnaissance ( 1 erreur de substitution ) et que l'ajout de paramètres labiaux n'entraine qu'une petite dégradation ( 2 erreurs de substitution supplémentaires).

Le modèle global s'avère être meilleur que le modèle Maître-Esclave ( 3 erreurs contre 5 ) mais nous devons observer que l'intervalle de confiance ne permet pas d'en tirer une conclusion définitive. De plus, étant donné la complexité du modèle Maître-Esclave, le nombre de ses paramètres est très important. Si nous prenons en compte le petit ensemble d'apprentissage dont nous disposons, nous ne pouvons espérer obtenir une bonne estimation de la totalité des paramètres.

R II / RéSULTATS SUR LE CORPUS DES LETTRES :

Cette deuxième évaluation sur le corpus des lettres épelées et connectées, nous permet d'examiner les performances du système afin de quantifier plus correctement l'apport des paramètres labiaux, dans les deux sortes de MMC.

Le premier MMC global est appris avec 8 coefficients cepstraux, l'Energie et la durée du segment. Nous avons ajouté successivement les paramètres labiaux et leurs dérivées. La même expérience a été répétée en initialisant le modèle global avec 8 coefficients cepstraux, leurs quatre premières dérivées, l'énergie ainsi que sa dérivée, et la durée du segment. Dans les deux cas, le nombre de lettres par phrase est imposé égal à 4.

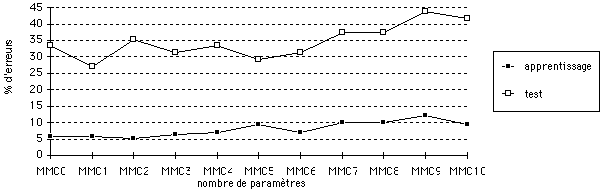
(a) taux d'erreurs en terme de phrases

(b) taux d'erreurs en terme de mots

MMC0 : 8 MFCC+E MMC6 : 8 MFCC+E+T+4 [[Delta]]MFCC+A+B

MMC1 : 8 MFCC+E+T MMC7 : 8 MFCC+E+T+A+B+S

MMC2 : 8 MFCC+E+T+4 [[Delta]]MFCC MMC8 : 8 MFCC+E+T+4 [[Delta]]MFCC+A+B+S

MMC3 : 8 MFCC+E+T+A MMC9 : 8 MFCC+E+T+A+B+S+[[partialdiff]]A+[[partialdiff]]B+[[partialdiff]]S

MMC4 : 8 MFCC+E+T+A+[[partialdiff]]A MMC10 : 8 MFCC+E+T+4 [[Delta]]MFCC

MMC5 : 8 MFCC+E+T+A+B +A+B+S+[[partialdiff]]A+[[partialdiff]]B+[[partialdiff]]S

Figure 6 : Taux d'erreurs avec le MMC global

Le meilleur taux de reconnaissance, à savoir 91,6 % (taux mots) est obtenu en utilisant la hauteur et la largeur des lèvres (figure 6, modèle MMC5). L'introduction de la surface des lèvres n'apporte pas d'information pertinente car elle est fortement corrélée aux paramètres A et B [Benoit 91]. Les dérivées des coefficients labiaux dégradent le taux de reconnaissance : une des causes principales peut être le manque de synchronisation entre les informations labiales et acoustiques, ou le manque de données d'apprentissage.

Le même protocole d'expérimentation est réalisé pour tester l'approche Maître/Esclave. Les coefficients labiaux A et B font partie des paramètres initiaux. Le nombre de lettres par phrases est imposé.

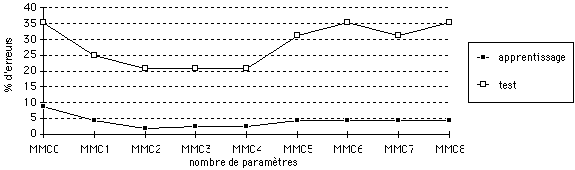
(a) taux d'erreurs en terme de phrases

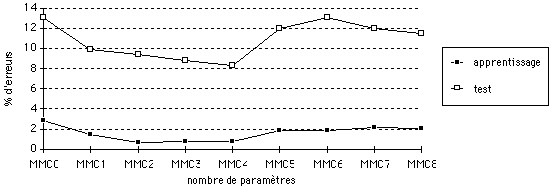
(b) taux d'erreurs en terme de mots

* MMC0 : 4 MFCC+A * MMC5 : 8 MFCC+E+T+4 [[Delta]]MFCC+A

* MMC1 : 8 MFCC+E+T+A * MMC6 : 8 MFCC+E+T+4 [[Delta]]MFCC+A+[[partialdiff]]A

* MMC2 : 8 MFCC+E+T+A+[[partialdiff]]A * MMC7 : 8 MFCC+E+T+4 [[Delta]]MFCC+A+B

* MMC3 : 8 MFCC+E+T+A+B * MMC8 : 8 MFCC+E+T+4 [[Delta]]MFCC+A+B+[[partialdiff]]A+[[partialdiff]]B

* MMC4 : 8 MFCC+E+T+A+B+[[partialdiff]]A+[[partialdiff]]B

Figure 7 : Taux d'erreurs avec le MMC Maître/Esclave

Le meilleur taux de reconnaissance est obtenu par les modèles MMC3 et MMC4, à savoir 91,7 % en terme de mots correctement reconnus. Lorsque le nombre de paramètres augmente, les performances décroissent, la cause est très certainement liée au relativement faible ensemble de données d'apprentissage par rapport au nombre de paramètres à apprendre.

R III/ RéSULTATS D'UNE RECONNAISSANCE SANS CONNAISSANCE DU NOMBRE DE LETTRES :

Nous avons repris le modèle Maître-Esclave MMC4 dans le cadre d'une expérience de reconnaissance des lettres épelées sans connaissance a priori du nombre de lettres prononcées :

* sur l'ensemble d'apprentissage, nous avons observé 3 substitutions, 6 insertions et 1 omission, ce qui correspond à un taux d'erreurs en termes de phrases, de 4,4 % (7 sur 158), et en termes de mots, de 1,6% (10 sur 632).

* sur l'ensemble de test, nous avons observé 13 substitutions, 11 insertions et 1 omission, ce qui correpond à un taux d'erreurs en termes de phrases, de 33,3 % (16 sur 48), et en termes de mots, de 13% (25 sur 192).

5 . Conclusion

Nous avons présenté deux approches probabilistes pour traiter la fusion de données acoustiques et articulatoires dans un but de reconnaissance. L'approche classique consiste à supposer indépendantes les informations issues des deux canaux tandis que l'approche maître-esclave exploite une certaine corrélation par l'intermédiaire de liens entre les lois d'observations.

Les deux approches modèle global et modèle maître-esclave donnent des résultats très comparables dans le cadre de la reconnaissance monolocuteur de suites de chiffres connectés ou de lettres épelées (92 % de taux de reconnaissance en mots). L'avantage de la deuxième méthode est liée à une meilleure compréhension du phénomène labial et offre des perspectives intéressantes :

-- Au niveau maître, nous augmenterons le nombre d'états de manière à se rapprocher des études statistiques qui ont montré l'émergence de visèmes [Benoit 91]

-- Le modèle maître-esclave est, dans son actuelle implémentation, fort simplifié et certaines hypothèses sont trop fortes : le passage d'un état ouvert à celui de fermé ne se réalise pas de manière instantannée! En fonction du volume croissant de l'ensemble d'apprentissage qui nous sera ultérieurement fourni, nous complexifierons le modèle simplifié pour tendre vers le modèle exact et tester ses réelles possibilités.

--L'étude d'une désynchronisation entre le labial et l'acoustique est plus abordable par cette approche.

L'utilisation des paramètres labiaux a pour but de rendre plus robuste la reconnaissance automatique de parole en milieu bruité ; nous avons montré que cette information ne dégradait absolument pas les performances des systèmes actuels déjà très performants. Nous sommes actuellement en cours d'évaluation des deux approches sur la même application en milieu bruité.

REFERENCES

[André-Obrecht, 88] R. André-Obrecht : A new statistical approach for the automatic segmentation of continuous speech signals, IEEE Trans. on Acoustics, Speech, Signal Processing, vol. 36, ndeg.1, janvier 1988.

[André-Obrecht, 93] R. André-Obrecht : Segmentation et parole? Habilitation à diriger des recherches, IRISA, Rennes, juin 1993.

[Benoit 91] C. Benoit, C. Abry, L.J. Boë : The effect of context on labiality in french. Eurospeech 91, Genova.

[Brugnara, 92] F. Brugnara, R. De Mori, D. Guiliani, M. Omologo : A family of Parallel Hidden Markov Models, ICASSP 92, San Francisco, 1992.

[Duchnowski 94] P. Duchnowski, U. Meier, A. Waibel : See me, hear me : integrating automatic speech recognition and lip-reading. S11-6.1 ICSLP 94, YOKOHAMA.

[Jacob 94] B. Jacob, R. André-Obrecht : Sub dictionary statistical modeling for isolated word recognition. ICSLP 94, YOKOHAMA

[Lallouache 91] T. Lallouache : Un poste "visage parole" couleur. Acquisition et traitement automatique des contours de lèvres. Thèse de doctorat de l'Institut National Polytechnique de Grenoble, 1991.