Gestion d'arbres par représentation intervallaire

Peu connue, la représentation intervallaire des arbres est une technique très performante.
Traditionnellement les représentations hiérarchiques font appel à des arborescenses modélisées par une table avec une autojointure entre la clef primaire des données mère et une clef secondaire relative aux données de la ligne fille. Cette simplicité a un coût élevé puisque la plupart des requêtes de recherche dans un tel arbre nécessitent un processus récursif, donc de la programmation dans un langage hôte ou dans une procédure stockée.
Avec la représentation intervallaire, toutes les recherches deviennent de simples requêtes basique et les performances sont sans communes mesure avec le modèle en autojointure.

Préambule
1. Représentation classique par auto-jointure
2. Représentation intervallaire des arborescense
2.1. Rechercher toutes les feuilles
2.2. Toutes les feuilles sous un élément de référence
2.3. Rechercher tous les noeuds
2.4. Tous les noeuds sous un élément de référence
2.5. Tous les éléments dépendant d'un élément de référence (sous arbre)
2.6. Tous les éléments indépendants d'un élément de référence (complément au sous arbre)
2.7. Tous les pères d'un élément de référence
2.8. Recherche de la racine de l'arbre
2.9. Compter les feuilles
2.10. Compter les noeuds
2.11. Insertion d'un élément dans cette arborescence
2.12. Suppression d'un élément de cette arborescence
2.13. Suppression d'un sous arbre
2.14. La cerise sur le gâteau !

Préambule

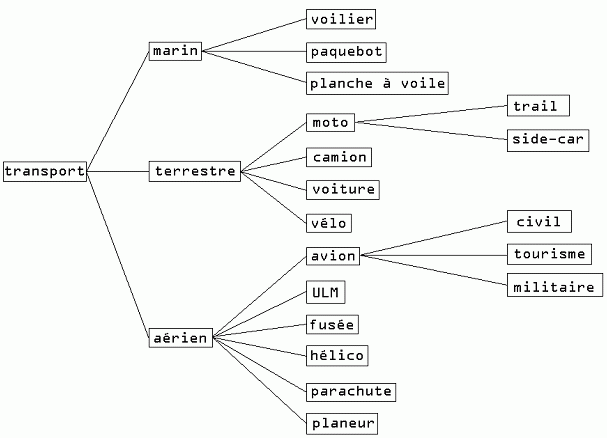
Voici un arbre dont les données représente des familles de véhicules :

1. Représentation classique par auto-jointure

Une manière habituelle de représenter un tel arbre est de prévoir une auto-jointure de la table sur elle-même :

CREATE TABLE FAMILLE
(FAM_ID   INTEGER,
 FAM_LIB  VARCHAR(16),
 FAM_PERE INTEGER)


INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (0, 'Transport', NULL)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (1, 'Terrestre', 0)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (2, 'Marin', 0)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (3, 'Aérien', 0)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (4, 'Voiture', 1)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (5, 'Camion', 1)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (6, 'Moto', 1)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (7, 'Vélo', 1)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (8, 'Hélico', 3)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (9, 'Avion', 3)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (10, 'ULM', 3)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (11, 'Fusée', 3)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (12, 'Parachute', 3)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (13, 'Planeur', 3)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (14, 'Voilier', 2)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (15, 'Paquebot', 2)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (16, 'Planche à voile', 2)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (17, 'Trail', 6)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (18, 'Side-car', 6)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (19, 'Civil', 9)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (20, 'Tourisme', 9)
INSERT INTO FAMILLE (FAM_ID, FAM_LIB, FAM_PERE)       VALUES (21, 'Militaire', 9)

Ici, c'est la colonne FAM_PERE qui permet de joindre l'élément de l'arbre à son ancètre.

Trouver le supérieur direct d'un élément n'est pas une chose difficile. Prenons par exemple le Parachute (ID = 12); la recherche du père s'effectue par la requête :


SELECT * 
FROM FAMILLE
WHERE FAM_ID = (SELECT FAM_PERE
                FROM FAMILLE
                WHERE FAM_ID = 12)


FAM_ID      FAM_LIB          FAM_PERE 
----------- ---------------- ----------- 
3           Aérien           0

Mais la recherche de tous les ascendants relève d'une autre paire de manche. En général elle passe par une procédure récursive du genre :


Procedure RecherchePeres (in id integer, inout reponse string)
begin
   reponse = reponse + ', ' + (SELECT FAM_LIB 
                               FROM FAMILLE
                               WHERE FAM_ID = ID)
if id = 0
then
   return
else
   id = (SELECT FAM_PERE 
         FROM FAMILLE
         WHERE FAM_ID = ID)
end

Or, non seulement la récursivité est très coûteuse, mais certains langages de procédures stockées, comme le Transact SQL de SQL Server de Microsoft ne savent pas la gérer !

C'est pourquoi ce modèle est a proscire lorsque :

l'arbre est profond (plus de 5 niveaux)
l'arbre est large (plus de 100 éléments sur un même niveau)
l'arbre contient beaucoup de valeurs (à partir de 200 à 300 éléments)
la majorité des requêtes sont des requêtes d'interrogation - SELECT (au moins 50% des requêtes)

Et personnellement je vous conseille de passer au modèle par intervalle dès que l'un de ces 4 critères est vrai !

2. Représentation intervallaire des arborescense

Une manière élégante et particulièrement performante de représenter les hiérarchies de type arborescentes est de créer des intervalles adjacents et recouvrant. Le principe est simple :

des feuilles situées au même niveau ont des intervalles adjacents
des noeuds englobant des feuilles ou d'autres nœuds ont des intervalles recouvrant

Rappelons aussi qu'un intervalle est constitué de deux valeurs : la borne basse et la borne haute.

Nous avons alors tout dit sur cette représentation hiérarchique... Mais quel en est l'intérêt ?
Si l'insertion ou la suppression dans une telle représentation est un peu coûteuse, l'interrogation et notamment la recherche s'exprime la plupart du temps en une seule requête, comme nous allons le voir...

Pour cette modélisation, nous devons donc attribuer à toutes les entrées de notre table arborescente les deux bornes de l'intervalle que nous appellerons BG (Borne Gauche) et BD (Borne Droite). L'attribution des valeurs de ces bornes se faisant en parcourant l'arbre comme si l'on traçait une ligne pour l'entourer au plus près sans jamais croiser cette ligne avec une branche et en numérotant séquentiellement chaque feuille ou nœud une première fois par le bord gauche et une seconde fois par le bord droit (ou par analogie avec une feuille sur le recto puis le verso) En fait on trace autour de 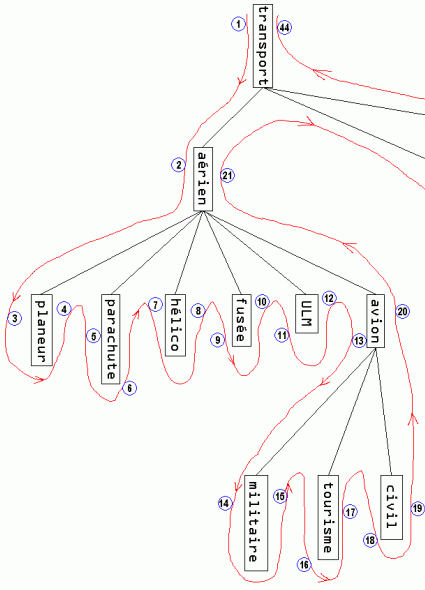l'arbre une ligne l'enveloppant au plus juste, comme ceci :

(Vous voudrez bien m'excuser pour avoir découpé cet arbre en deux, mais c'était pas facile de travailler ce dessin en un seul plan !)
Numérotation par intervalle des nœuds et feuilles de l'arbres en utilisant un tracé "enveloppant"

Sur cette figure, on peut déjà constater que :

le nombre de numéro attribué est le double du nombre d'éléments
toutes les feuilles ont un intervalle de longueur 1 (borne droite - borne gauche = 1)
a contrario, tous les noeuds ont un intervalle de longueur supérieur à 1 (borne droite - borne gauche > 1)

Nous pouvons donc immédiatement savoir si tel ou tel élément de l'arborescence est un nœud ou une feuille.

Mais il y a aussi plus fort : nous pouvons en une seule requête ramener :

tous les éléments, nœuds et feuille confondus, dépendant de l'élément de référence (c'est à dire le sous arbre dont la racine est l'élément de référence)
tous les éléments indépendants de l'élément de référence (le ou les sous arbres complémentaires)
tous les pères d'un élément de référence

Une autre façon de "voir" cet arbre est de le représenter par tranches englobantes. La racine est la tranche la plus large, et chaque feuille est une tranche fine :

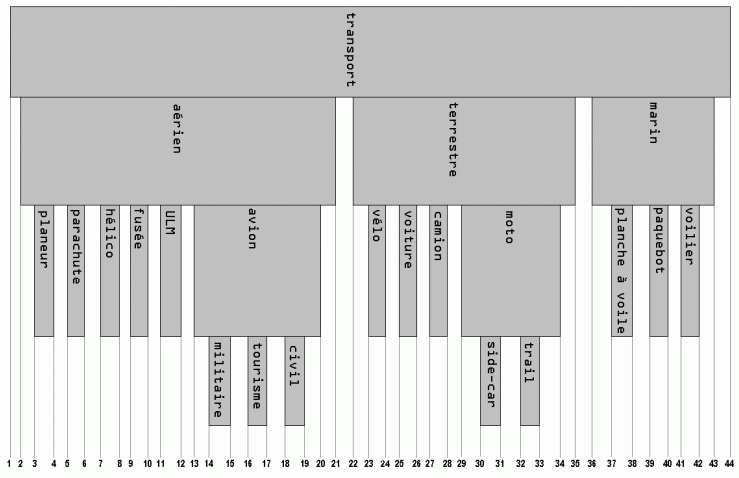représentation par tranche d'un arbre modélisé de façon intervallaire

Construisons le jeu d'essai pour tester nos requêtes :


CREATE TABLE NEW_FAMILLE
(NFM_BG  INTEGER,
 NFM_BD  INTEGER,
 NFM_LIB VARCHAR(16))


INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (1, 44, 'Transport')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (2, 21, 'Aérien')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (3, 4, 'Planeur')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (5, 6, 'Parachute')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (7, 8, 'Hélico')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (9, 10, 'Fusée')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (11, 12, 'ULM')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (13, 20, 'Avion')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (14, 15, 'Militaire')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (16, 17, 'Tourisme')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (18, 19, 'Civil')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (22, 35, 'Terrestre')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (23, 24, 'Vélo')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (25, 26, 'Voiture')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (27, 28, 'Camion')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (29, 34, 'Moto')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (30, 31, 'Side-car')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (32, 33, 'Trail')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (36, 43, 'Marin')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (37, 38, 'Planche à voile')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (39, 40, 'Paquebot')
INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)       VALUES (41, 42, 'Voilier')

Voici maintenant comment s'exprime les principales requêtes de gestion de ce modèle d'arbre :

2.1. Rechercher toutes les feuilles

Il s'agit simplement de rechercher les éléments dont la longueur de l'intervalle vaut un :


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BD - NFM_BG = 1


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
3           4           Planeur
5           6           Parachute
7           8           Hélico
9           10          Fusée
11          12          ULM
14          15          Militaire
16          17          Tourisme
18          19          Civil
23          24          Vélo
25          26          Voiture
...

2.2. Toutes les feuilles sous un élément de référence

Dans ce cas il faut restreindre la plage de recherche des bords à ceux de l'élément, toujours en recherchant les intervalles de longueur un.

Exemple: toutes les feuilles sous l'élément 'Terrestre' dont les bords droit et gauche sont : NFM_BG = 22 et NFM_BD = 35


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BD - NFM_BG = 1
   AND NFM_BG > 22
   AND NFM_BD < 35


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
23          24          Vélo
25          26          Voiture
27          28          Camion
30          31          Side-car
32          33          Trail

2.3. Rechercher tous les noeuds

Il suffit de rechercher tous les éléments dont la longueur de l'intervalle est supérieure à un :


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BD - NFM_BG > 1


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
1           44          Transport
2           21          Aérien
13          20          Avion
22          35          Terrestre
29          34          Moto
36          43          Marin

2.4. Tous les noeuds sous un élément de référence

En plus de chercher les éléments dont la longueur de l'intervalle est supérieure à un, il faut aussi restreindre la plage de recherche des bords à ceux de l'élément considéré.

Exemple: tous les noeuds sous l'élément 'Transport' dont NFM_BG vaut 1 et NFM_BD vaut 44


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BD - NFM_BG > 1
   AND NFM_BG > 1
   AND NFM_BD < 44


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
2           21          Aérien
13          20          Avion
22          35          Terrestre
29          34          Moto
36          43          Marin

2.5. Tous les éléments dépendant d'un élément de référence (sous arbre)

Il s'agit simplement de rechercher des éléments dont les bords gauche et droit sont inclus dans les bords gauche et droite de l'élément considéré.

Exemple : tous les éléments dépendant de l'élément 'Terrestre' dont NFM_BG vaut 22 et NFM_BD vaut 35


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BG > 22
   AND NFM_BD < 35


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
23          24          Vélo
25          26          Voiture
27          28          Camion
29          34          Moto
30          31          Side-car
32          33          Trail

Cette requête retient les éléments hiérarchiquement dépendant de l'élément 'Terrestre', mais en l'excluant, tandis que la requête suivante :


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BG >= 22
   AND NFM_BD <= 35


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
22          35          Terrestre
23          24          Vélo
25          26          Voiture
27          28          Camion
29          34          Moto
30          31          Side-car
32          33          Trail

Retient même l'élément de référence qui devient alors la racine de ce sous arbre.

2.6. Tous les éléments indépendants d'un élément de référence (complément au sous arbre)

Il s'agit simplement de retenir tous les éléments dont le bord gauche est inférieur au bord gauche de l'élément de référence ainsi que ceux dont le bord droit est supérieur au bord droit de l'élément de référence.

Exemple : tous les éléments indépendants de l'élément terrestre dont NFM_BG vaut 22 et NFM_BD vaut 35


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BG < 22
    OR NFM_BD > 35


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
1           44          Transport
2           21          Aérien
3           4           Planeur
5           6           Parachute
7           8           Hélico
9           10          Fusée
11          12          ULM
13          20          Avion
14          15          Militaire
16          17          Tourisme
18          19          Civil
36          43          Marin
37          38          Planche à voile
39          40          Paquebot
41          42          Voilier

On peut remarquer qu'en inversant les critères on obtient de recherche on obtient les compléments aux sous arbres en excluant tous les pères de l'élément considéré :


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BG > 35
    OR NFM_BD < 22


NFM_BG      NFM_BD      NFM_LIB 
----------- ----------- ---------------- 
2           21          Aérien
3           4           Planeur
5           6           Parachute
7           8           Hélico
9           10          Fusée
11          12          ULM
13          20          Avion
14          15          Militaire
16          17          Tourisme
18          19          Civil
36          43          Marin
37          38          Planche à voile
39          40          Paquebot
41          42          Voilier

2.7. Tous les pères d'un élément de référence

En fait on recherche tous les éléments incluant à la fois les bords gauche et droit de l'élément de référence :

Exemple : tous les pères de l'élément 'Moto' dont le NFM_BG vaut 29 et le NFM_BD vaut 34


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BG < 29
   AND NFM_BD > 34


NFM_BG      NFM_BD      NFM_LIB
----------- ----------- ----------------
3           46          Transport
24          37          Terrestre

2.8. Recherche de la racine de l'arbre

Si toutes les insertions sont toujours faites par la droite, la racine possède un intervalle dont le bord gauche vaut un :


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BG = 1

Dans le cas contraire, on peut retrouver la racine par la requête, c'est à dire que l'on recherche l'élément dont la longueur de l'intervalle à une unité près est le double du nombre d'éléments :


SELECT *
FROM   NEW_FAMILLE
WHERE  (NFM_BD - NFM_BG + 1) / 2 = (SELECT COUNT(*)
                                    FROM NEW_FAMILLE)


NFM_BG      NFM_BD      NFM_LIB
----------- ----------- ----------------
1           44          Transport

On peut aussi, plus simplement, rechercher l'élément qui a la plus grande longueur d'intervalle :


SELECT *
FROM NEW_FAMILLE
WHERE  (NFM_BD - NFM_BG) = (SELECT MAX(NFM_BD - NFM_BG)
                            FROM NEW_FAMILLE)

Qui, bien entendu, conduit au même résultat.

2.9. Compter les feuilles

Il s'agit de compter les éléments pour lesquels la longueur de l'intervalle vaut un :


SELECT COUNT(*) AS FEUILLES
FROM NEW_FAMILLE
WHERE NFM_BG = NFM_BD -1


FEUILLES
-----------
16

NOTA : ici nous avons fait une petite variante dans le filtre WHERE. Plutôt que de préciser NFM_BD - NFM_BG = 1, nous avons passé l'élément NFM_BD du côté droit du signe égal, ce qui ne change rien à la valeur de l'équation, mais permet d'activer l'index de la colonne NFM_BG, si index il y a, ce que l'on peut supposer puisqu'il faut bien une clef à cette table !

2.10. Compter les noeuds

Compter les nœuds procède de l'énumération des lignes dont la valeur de l'intervalle est supérieure ou différente de un :


SELECT COUNT(*) AS NOEUDS
FROM NEW_FAMILLE
WHERE NFM_BG <> NFM_BD -1


NOEUDS
-----------
6

2.11. Insertion d'un élément dans cette arborescence

La particularité de cette représentation arborescente est qu'il s'agit d'un arbre orienté pour lequel nous pouvons choisir d'insérer à gauche ou à droite de l'élément père. Si cela n'a pas d'importance, choisissons systématiquement l'insertion à droite qui permet de ne pas avoir besoin de générer des valeurs négatives pour nos bornes et laisse la racine avec un bord gauche valant un ce qui permet de retrouver la racine instantanément.

Tentons d'insérer l'élément 'Roller' en liaison directe avec son père l'élément 'Terrestre'. Dans ce cas, la borne droite de l'élément 'Terrestre' servira de référence puisque nous insérons à droite. Cette borne droite vaut 35.
Les ordres d'insertion sont alors les suivants :


UPDATE NEW_FAMILLE
SET NFM_BD = NFM_BD + 2
WHERE NFM_BD >= 35


UPDATE NEW_FAMILLE
SET NFM_BG = NFM_BG + 2
WHERE NFM_BG >= 35


INSERT INTO NEW_FAMILLE (NFM_BG, NFM_BD, NFM_LIB)
       VALUES (35, 36, 'Roller')

En fait on décale de deux unités tous les bords, droits ou gauches, sans distinction aucune, dont la valeur est supérieure ou égale à la borne droite du père visé par l'insertion.
Une autre façon de voir les choses est de dire que l'intervalle du père visé par l'élément à insérer, grossit de deux unités pour absorber le nouveau fils et que cela conduit tous les bords situés à droite du père à un décalage de deux unités.

Il n'est pas possible de réaliser l'update en une seule requête. De plus si vous avez mis une contrainte d'unicité sur les bornes, il est impératif de commence par la mise à jour des bornes droite, puis celles de gauche et enfin l'insertion.

Bien entendu il vaut mieux gérer ces ordres SQL au sein d'une transaction.

2.12. Suppression d'un élément de cette arborescence

On peut y arriver simplement en supprimant la ligne correspondant à l'élément considéré.

Exemple : suppression de l'élément 'ULM' (dont le NFM_BG vaut 11) :


DELETE FROM NEW_FAMILLE
WHERE NFM_BG = 11

Néanmoins cela laisse un arbre avec des trous dans la gestion unitaire des intervalles. Cela n'est pas beau, mais surtout cela peut affecter certaines des requêtes que nous avons vues. La correction de ce défaut est d'une grande simplicité. Il s'agit de renuméroter une partie de l'arbre. Cela se fait en considérant la valeur du bord gauche de l'élément à supprimer et par conséquent de décaler tous les bords (gauche ou droits) supérieur à cette valeur de deux unités vers la gauche (soit -2).
Dans le cadre de notre exemple, le bord gauche valant 11, il convient d'exécuter les requêtes de modification suivante :


UPDATE NEW_FAMILLE
SET    NFM_BG = NFM_BG - 2
WHERE  NFM_BG >= 11


UPDATE NEW_FAMILLE
SET    NFM_BD = NFM_BD - 2
WHERE  NFM_BD >= 11

De la même façon, Il n'est pas possible de réaliser les updates en un seul ordre et la suppression doit intervenir en premier sinon il y a risque de téléscopage des valeurs de bornes. De plus si vous avez mis une contrainte d'unicité sur les bornes, il est impératif de commence par la mise à jour des bornes gauche, puis celles de droite.

2.13. Suppression d'un sous arbre

La suppression d'un sous arbre complet n'est pas plus difficile que la suppression d'une feuille. On peut donc y arriver en une seule requête ou encore, choisir de faire propre et renuméroter l'arbre.

Supprimons par exemple le sous arbre ayant pour racine l'élément 'Terrestre' de borne gauche 22 et de borne droite 35 :


DELETE FROM NEW_FAMILLE
WHERE  NFM_BG >= 22
   AND NFM_BD <= 35

Renumérotons alors les bornes situées à droite du sous arbre supprimé, avec un décalage de : 35 - 22 + 1, soit 14


UPDATE NEW_FAMILLE
SET NFM_BD = NFM_BD - 14
WHERE NFM_BD >= 22


UPDATE NEW_FAMILLE
SET NFM_BG = NFM_BG - 14
WHERE NFM_BG > 22

Bien entendu l'insertion d'un sous arbre (opération beaucoup plus rare) est aussi simple qu'est la suppression d'un sous arbre.

2.14. La cerise sur le gâteau !

Quelques requêtes peuvent encore apparaître plus difficile, notamment lorsqu'il s'agit de chercher des éléments relatifs à un niveau de l'arbre. Par exemple la recherche des feuilles situées au niveau n-1 par rapport au niveau n de l'élément de référence. Mais si ce type de requête risque d'être votre pain quotidien, rien n'empêche de modéliser le niveau de l'élément au sein même de la table contenant l'arbre. Dans ce cas, la table devient :


CREATE TABLE NEW_FAMILLE
(NFM_BG  INTEGER,
 NFM_BD  INTEGER,
 NFM_NV  INTEGER,
 NFM_LIB VARCHAR(16))

NFM_NV contenant le niveau de l'élément, en commençant par le niveau zéro, c'est à dire l'élément racine de l'arbre. Dès lors les modifications à effectuer pour que les requêtes vues tiennent compte du niveau des éléments deviennent triviales.

Par exemple, pour la recherche des feuilles de niveau n + 1 par rapport à l'élément 'Terrestre', la requête s'écrit :


SELECT *
FROM   NEW_FAMILLE
WHERE  NFM_BD - NFM_BG = 1
   AND NFM_BG > 22
   AND NFM_BD < 35
   AND NFM_NV = 2

Je vous laisse deviner l'écriture des autres requêtes...

IMPORTANT :
Pour tester l'unicité des valeurs des bornes qui se trouvent dans deux colonnes distinctes, on peut utiliser des contraintes de table telles que :


CONSTRAINT UNI_BORNE CHECK BORNE_DROITE 
(VALUE NOT IN
(SELECT BORNE_DROITE  AS BORNE
 FROM   MaTable
 UNION  ALL
 SELECT BORNE_GAUCHE  AS BORNE
 FROM   MaTable))

et :

CONSTRAINT UNI_BORNE CHECK BORNE_GAUCHE 
(VALUE NOT IN
(SELECT BORNE_DROITE  AS BORNE
 FROM   MaTable
 UNION  ALL
 SELECT BORNE_GAUCHE  AS BORNE
 FROM   MaTable))

Mais peu de SGBDR acceptent des contraintes si complexes et il est souvent nécessaire de passer par des triggers pour appliquer une telle intégrité.

PROCÉDURES STOCKÉES DE MANIPULATION DES ARBRES :

On trouvera sur le site un exemple des principales procédures stockées écrites en Transact SQL (MS) pour gérer les insertions et suppression dans un tel arbre.

Voici un exemple (pour SQL Server) de gestion d'un arbre de nomenclature avec niveau.

ordre de création de la table
les deux procédures pour insérer et pour supprimer
la vue simplifiant la présentation des données


-- création de la table T_NOMENCLATURE_NMC
create table T_NOMENCLATURE_NMC
(   NMC_ID                       INTEGER               identity,
    NMC_LIBELLE                  CHAR(32)              not null,
    NMC_DESCRIPTION              VARCHAR(1024)         null    ,
    NMC_NIVEAU                   INTEGER               not null,
    NMC_BG                       INTEGER               not null,
    NMC_BD                       INTEGER               not null,
    constraint PK_T_NOMENCLATURE_NMC primary key (NMC_ID))


-- indexation de la table
CREATE INDEX NDX_NMC_BG ON T_NOMENCLATURE_NMC (NMC_BG)
CREATE INDEX NDX_NMC_BD ON T_NOMENCLATURE_NMC (NMC_BD)


-- procédure d'insertion dans l'arbre [Frédéric Brouard, Philippe Boucault 25/09/2002]

CREATE PROCEDURE SP_INS_NOMENCLATURE

      @lib varchar(32),     -- le libellé à insérer
      @desc varchar(1024),  -- la description à insérer
      @id_parent int,       -- Ancêtre ou frère point d'origine de l'insertion 
      @mode char(2)         -- le mode d'insertion :
                                    -- FA : Fils Ainé,
                                    -- FC : Fils Cadet,
                                    -- GF : Grand frère,
                                    -- PF : Petit Frère,
                                    -- P  : Père
AS

 DECLARE @OK int

 DECLARE @bgp int          -- borne gauche parent
 DECLARE @bdp int          -- borne droite parent 
 DECLARE @nivp int         -- niveau parent 

 DECLARE @bgi int          -- borne gauche à insérer
 DECLARE @bdi int          -- borne droite à insérer
 DECLARE @nivi int         -- niveau à insérer

 SET NOCOUNT ON

-- gestion des effets de bord
 IF @mode IS NULL OR @lib IS NULL OR @lib = ''
 BEGIN
    RAISERROR ('Insertion impossible sans libellé ou mode ! (TABLE T_NOMENCLATURE_NMC)', 16, 1)
    RETURN
 END

 SET @mode = UPPER(@mode)
 IF NOT( @mode = 'FA' OR @mode = 'FC' OR @mode = 'GF' OR @mode = 'PF'  OR @mode = 'P')
 BEGIN
    RAISERROR ('Insertion impossible, mode inconnu !', 16, 1)
    RETURN
 END

 -- démarrage transaction 
 SET TRANSACTION ISOLATION LEVEL SERIALIZABLE 
 BEGIN TRANSACTION INSERT_NOMENCLATURE
 

-- pas de parent => seul cas, table vide ou insertion d'un collatéral 
 IF @id_parent IS NULL
 BEGIN
    SELECT @OK = count(*) FROM T_NOMENCLATURE_NMC
    IF @OK = 0 OR @OK IS NULL
    BEGIN
       IF @mode = 'FA' OR @mode = 'FC'
       BEGIN
          RAISERROR ('Insertion impossible dans un arbre pour un fils sans père !', 16, 1)
          GOTO LBL_ERROR
          RETURN
       END
       ELSE
       BEGIN
-- première insertion 
          INSERT INTO T_NOMENCLATURE_NMC ( NMC_LIBELLE, NMC_DESCRIPTION, NMC_NIVEAU, NMC_BG, NMC_BD )
                 VALUES( @lib, @desc, 0, 1, 2 )
          IF @@ERROR <> 0
          BEGIN
             GOTO LBL_ERROR
             RETURN
          END
          COMMIT TRANSACTION INSERT_NOMENCLATURE
          SELECT @@IDENTITY
          RETURN
       END
    END
    ELSE 
-- Insertion d'un collatéral 
    BEGIN 
       RAISERROR ('Insertion impossible dans un arbre pour un collatéral sans précision du parent !', 16, 1)
       GOTO LBL_ERROR
       RETURN
    END
 END

-- Le parent existe toujours ?
 SELECT @OK = count(*) FROM T_NOMENCLATURE_NMC WHERE NMC_ID = @id_parent
 IF @OK = 0 OR @OK IS NULL
 BEGIN
    RAISERROR ('Insertion impossible, le parent n''existe plus !', 16, 1)
    GOTO LBL_ERROR
    RETURN
 END

-- On a un parent : on récupère ses éléments
 SELECT @bgp = NMC_BG, @bdp = NMC_BD, @nivp = NMC_NIVEAU 
        FROM T_NOMENCLATURE_NMC 
        WHERE NMC_ID = @id_parent

-- insertion d'un père
 IF @mode = 'P'
 BEGIN
    -- Décalage de l'ensemble colatéral droit
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BD = NMC_BD + 2
           WHERE NMC_BD > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG + 2
           WHERE NMC_BG > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    -- Décalalage ensemble visé vers le bas
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG + 1,
               NMC_BD = NMC_BD + 1,
               NMC_NIVEAU = NMC_NIVEAU + 1
           WHERE NMC_BG >= @bgp AND NMC_BD <= @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    -- Insertion du nouveau père
    INSERT INTO T_NOMENCLATURE_NMC ( NMC_LIBELLE, NMC_DESCRIPTION, NMC_NIVEAU, NMC_BG, NMC_BD )
           VALUES( @lib, @desc, @nivp, @bgp, @bdp + 2 )
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
 END

-- Insertion d'un grand frère
 IF @mode = 'GF'
 BEGIN
    -- Limite sup.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BD = NMC_BD + 2
           WHERE NMC_BD > @bgp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    -- Limite inf.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG + 2
           WHERE NMC_BG >= @bgp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    SET @bgi = @bgp
    SET @bdi = @bgp + 1
    SET @nivi = @nivp
    INSERT INTO T_NOMENCLATURE_NMC ( NMC_LIBELLE, NMC_DESCRIPTION, NMC_NIVEAU, NMC_BG, NMC_BD )
           VALUES( @lib, @desc, @nivi, @bgi, @bdi )
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
 END
 

--  Insertion d'un petit frère 
 IF @mode = 'PF'
 BEGIN
    -- Limite sup.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BD = NMC_BD + 2
           WHERE NMC_BD > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    -- Limite inf.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG + 2
           WHERE NMC_BG >= @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    SET @bgi = @bdp + 1
    SET @bdi = @bdp + 2
    SET @nivi = @nivp
    INSERT INTO T_NOMENCLATURE_NMC ( NMC_LIBELLE, NMC_DESCRIPTION, NMC_NIVEAU, NMC_BG, NMC_BD )
           VALUES( @lib, @desc, @nivi, @bgi, @bdi )
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
 END

--  Insertion d'un fils ainé
 IF @mode = 'FA'
 BEGIN
    -- Limite sup.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BD = NMC_BD + 2
           WHERE NMC_BD > @bgp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    -- Limite inf.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG + 2
           WHERE NMC_BG > @bgp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    SET @bgi = @bgp + 1
    SET @bdi = @bgp + 2
    SET @nivi = @nivp + 1
    INSERT INTO T_NOMENCLATURE_NMC ( NMC_LIBELLE, NMC_DESCRIPTION, NMC_NIVEAU, NMC_BG, NMC_BD )
           VALUES( @lib, @desc, @nivi, @bgi, @bdi )
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
 END

--  Insertion d'un fils cadet
 IF @mode = 'FC'
 BEGIN
    -- Limite sup.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BD = NMC_BD + 2
           WHERE NMC_BD >= @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    -- Limite inf.
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG + 2
           WHERE NMC_BG > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END

    SET @bgi = @bdp
    SET @bdi = @bdp + 1
    SET @nivi = @nivp + 1
    INSERT INTO T_NOMENCLATURE_NMC ( NMC_LIBELLE, NMC_DESCRIPTION, NMC_NIVEAU, NMC_BG, NMC_BD )
           VALUES( @lib, @desc, @nivi, @bgi, @bdi )
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
 END

-- renvoi de l'identifiant de l'élément inséré
 SELECT @@IDENTITY

 COMMIT TRANSACTION INSERT_NOMENCLATURE
 RETURN

 LBL_ERROR:
 ROLLBACK TRANSACTION INSERT_NOMENCLATURE


-- procédure de suppression dans l'arbre [Frédéric Brouard, Philippe Boucault 25/09/2002]

CREATE PROCEDURE SP_DEL_NOMENCLATURE

      @id int,               -- l'identifiant cible de le suppression
      @recurs bit            -- le mode de suppression (récursif ou non) :
                                     -- 0 => on ne supprime que cet élément et on conserve le sous arbre
                                     -- 1 => on supprime cet élément et le sous arbre

AS

 DECLARE @OK int

 DECLARE @bgp int            -- borne gauche de la cible
 DECLARE @bdp int            -- borne droite de la cible

 DECLARE @delta int          -- écart introduit par la suppression du sous arbre

 SET NOCOUNT ON

-- gestion des effets de bord
 IF @id IS NULL
 BEGIN
    RAISERROR ('Suppression impossible sans identifiant défini !', 16, 1)
    RETURN
 END

 IF @recurs IS NULL
 BEGIN
    RAISERROR ('Suppression impossible sans indication de récursion !', 16, 1)
    RETURN
 END

-- démarrage transaction 
 SET TRANSACTION ISOLATION LEVEL SERIALIZABLE 
 BEGIN TRANSACTION DELETE_NOMENCLATURE

-- Il existe toujours ?
 SELECT @OK = count(*) FROM T_NOMENCLATURE_NMC WHERE NMC_ID = @id
 IF @OK = 0 OR @OK IS NULL
 BEGIN
    RAISERROR ('Suppression impossible, élément inexistant ! (TABLE T_NOMENCLATURE_NMC)', 16, 1)
    GOTO LBL_ERROR
    RETURN
 END

-- récupération des bornes cible
 SELECT @bgp = NMC_BG, @bdp = NMC_BD
        FROM T_NOMENCLATURE_NMC 
        WHERE NMC_ID = @id
 IF @@ERROR <> 0
 BEGIN
    GOTO LBL_ERROR
    RETURN
 END

-- Suppression récursive ?
 IF @recurs = 1
 BEGIN
-- OUI ! tout le sous arbre doit être supprimé
    -- Calcul du Delta
    SET @delta = @bdp - @bgp + 1
    -- suppression de tous les éléments
    DELETE FROM T_NOMENCLATURE_NMC
           WHERE NMC_BG >= @bgp
           AND NMC_BD <= @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
    -- décalage des bornes gauche
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG - @delta
           WHERE NMC_BG > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
    -- décalage des bornes droites
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BD = NMC_BD - @delta
           WHERE NMC_BD > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
 END
 ELSE
 BEGIN
-- NON ! on ne supprime que l'élément
    -- suppression de l'élément
    DELETE FROM T_NOMENCLATURE_NMC
           WHERE NMC_ID = @id
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
    -- décalage des bornes et niveau de l'arbre sous l'élément supprimé
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG - 1,
               NMC_BD = NMC_BD - 1,
               NMC_NIVEAU = NMC_NIVEAU - 1
           WHERE NMC_BG > @bgp
           AND NMC_BD &lt; @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
    -- décalage des bornes gauches des éléments situés à droite de l'élément supprimé
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BG = NMC_BG - 2
           WHERE NMC_BG > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
    -- décalage des bornes droites des éléments situés à droite de l'élément supprimé
    UPDATE T_NOMENCLATURE_NMC
           SET NMC_BD = NMC_BD - 2
           WHERE NMC_BD > @bdp
    IF @@ERROR <> 0
    BEGIN
       GOTO LBL_ERROR
       RETURN
    END
 END

 COMMIT TRANSACTION DELETE_NOMENCLATURE
 RETURN

 LBL_ERROR:
 ROLLBACK TRANSACTION DELETE_NOMENCLATURE
 RETURN


-- requête réalisant la vue de synthèse :
CREATE VIEW V_NOMENCLATURE_NMC
AS
SELECT NMC_ID, CAST(SPACE(NMC_NIVEAU)+ NMC_LIBELLE AS VARCHAR(64)) AS NMC_LIBELLE,
       NMC_NIVEAU, NMC_BG, NMC_BD,
       (SELECT COUNT(*)
        FROM   T_NOMENCLATURE_NMC T2
        WHERE  T2.NMC_BG > T1.NMC_BG
          AND  T2.NMC_BD < T1.NMC_BD) AS NMC_NBR_DESCENDANT,
       NMC_DESCRIPTION 
FROM   T_NOMENCLATURE_NMC T1


-- jeu de données test : insertion dans l'arbre de la nomenclature suivante
METHODES
   MERISE
      Power Designor
   UML
      Rational Rose
LANGAGES
   Pascal
      Delphi
   Basic
      MS Visual Basic
   ASP
   PHP
   SQL Intégrés 
      MS Transact SQL
      Oracle PL/SQL
      InterBase ISQL
SGBDR
   Microsoft
      Access
      SQL Server
         SQL Server 7
         SQL Server 2000
         MSDE
   Borland
      InterBase
   Oracle
   IBM
      DB2


SP_INS_NOMENCLATURE 'METHODES', NULL, NULL, 'GF'


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           2           0


SP_INS_NOMENCLATURE 'MERISE', NULL, 1 , 'FA'


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           4           1
2            MERISE                          1           2           3           0


SP_INS_NOMENCLATURE 'Power Designor', NULL, 2 , 'FA'


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           6           2
2            MERISE                          1           2           5           1
3             Power Designor                 2           3           4           0


SP_INS_NOMENCLATURE 'Rational Rose', NULL, 3 , 'PF'


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           8           3
2            MERISE                          1           2           7           2
3             Power Designor                 2           3           4           0
4             Rational Rose                  2           5           6           0


SP_INS_NOMENCLATURE 'UML', NULL, 4 , 'P'


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           10          4
2            MERISE                          1           2           9           3
3             Power Designor                 2           3           4           0
5             UML                            2           5           8           1
4              Rational Rose                 3           6           7           0


SP_DEL_NOMENCLATURE 5, 1


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           6           2
2            MERISE                          1           2           5           1
3             Power Designor                 2           3           4           0


SP_INS_NOMENCLATURE 'UML', NULL, 2 , 'PF'


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           8           3
2            MERISE                          1           2           5           1
3             Power Designor                 2           3           4           0
6            UML                             1           6           7           0


SP_INS_NOMENCLATURE 'Rational Rose', NULL, 6 , 'FA'


NMC_ID      NMC_LIBELLE                      NMC_NIVEAU  NMC_BG      NMC_BD      NMC_NBR_DESCENDANT 
----------- -------------------------------- ----------- ----------- ----------- ------------------ 
1           METHODES                         0           1           10          4
2            MERISE                          1           2           5           1
3             Power Designor                 2           3           4           0
6            UML                             1           6           9           1
7             Rational Rose                  2           7           8           0


etc...

La cerise sur le gâteau...
Voici une vue permettant de réaliser un flux XML de l'arbre :


CREATE VIEW V_TREE_XML_NOMENCLATURE_TXN
AS
SELECT TOP 100 PERCENT WITH TIES BORNE, LIGNE
FROM   (SELECT -1 AS BORNE, CAST('<?xml version="1.0" encoding="ISO-8859-1"?>'
               AS VARCHAR(1024)) AS LIGNE
        FROM   V_NOMENCLATURE_NMC
        WHERE  NMC_ID = (SELECT MIN(NMC_ID) FROM V_NOMENCLATURE_NMC)
        UNION
        SELECT 0 AS NMC_BG, CAST('<document>' AS VARCHAR(1024)) AS LIGNE
        FROM   V_NOMENCLATURE_NMC
        WHERE  NMC_ID = (SELECT MIN(NMC_ID) FROM V_NOMENCLATURE_NMC)
        UNION 
        SELECT NMC_BG AS BORNE, SPACE(NMC_NIVEAU) 
               + '<TreeNode><Data LV="'+ CAST(NMC_NIVEAU AS VARCHAR(5))+'"'
               + ' BG="'+CAST(NMC_BG AS VARCHAR(5))+'"'
               + ' BD="'+CAST(NMC_BD AS VARCHAR(5))+'"'
               + ' ID="'+CAST(NMC_ID AS VARCHAR(5))+'"><Name>'
               + RTRIM(LTRIM(NMC_LIBELLE))+'</Name>' AS LIGNE
        FROM   V_NOMENCLATURE_NMC
        UNION 
        SELECT NMC_BD, CAST(SPACE(NMC_NIVEAU) + '</Data></TreeNode>' AS VARCHAR(1024))
        FROM   V_NOMENCLATURE_NMC 
        UNION
        SELECT (SELECT MAX(NMC_BD) + 1 FROM V_NOMENCLATURE_NMC) AS NMC_BG,
               CAST('</document>' AS VARCHAR(1024)) AS LIGNE
        FROM   V_NOMENCLATURE_NMC
        WHERE  NMC_ID = (SELECT MIN(NMC_ID) FROM V_NOMENCLATURE_NMC)) T
ORDER BY BORNE


SELECT LIGNE
FROM V_TREE_XML_NOMENCLATURE_TXN


LIGNE                                                                                                
---------------------------------------------------------------------------------------------------- 
<?xml version="1.0" encoding="ISO-8859-1"?>
<document>
<TreeNode><Data LV="0" BG="1" BD="10" ID="1"><Name>METHODES</Name>
 <TreeNode><Data LV="1" BG="2" BD="5" ID="2"><Name>MERISE</Name>
  <TreeNode><Data LV="2" BG="3" BD="4" ID="3"><Name>Power Designor</Name>
  </Data></TreeNode>
 </Data></TreeNode>
 <TreeNode><Data LV="1" BG="6" BD="9" ID="6"><Name>UML</Name>
  <TreeNode><Data LV="2" BG="7" BD="8" ID="7"><Name>Rational Rose</Name>
  </Data></TreeNode>
 </Data></TreeNode>
</Data></TreeNode>
</document>