Projet de formation

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

BALDET Christophe

HADDADI Youssef

HANNOUN Mohammed

LE MOULLAC Julien

 

 

 

 

 

 

 

 

PREAMBULE

STAR-CD ET CD ADAPCO

 

 

 

Le groupe CD-adapco, est l’un des Leaders mondiaux de la mécanique des fluides dans le domaine automobile, grâce à STAR-CD.

Ce secteur à l’avantage de présenter des applications très variées et très représentatives des problèmes d’écoulement et/ou de thermique que l’on retrouve dans l’industrie.

Au-delà du marché automobile, de nombreux clients de STAR-CD et de ses services se retrouve dans des secteurs aussi divers que l’énergie, les turbomachines, l’aéronautique, la chimie et les procédés, le biomédical, le ferroviaire, le génie civil, l’offshore et la marine, l’environnement, la pharmacie, l’électronique, l’électroménager et toute autre application industrielle.

La dernière version de Star-CD est une solution logicielle intégrée avec un modeleur paramétrique de toute dernière génération, un mailleur automatique, qui fonctionnent sous les deux grands systèmes d’exploitation ( Windows et Unix ). Ses solveurs sont reconnus comme les plus rapides du marché pour les problèmes instationnaires et tirent un avantage considérable des architectures en cluster.

CD Adapco Group est spécialisé dans le développement de logiciels de simulation en mécanique des fluides et milieux continus et réalise de la sous-traitance en engineering.

CD Adapco Group compte 300 employés parmi lesquels de nombreux spécialistes bénéficiant d'une grande expertise en Mécanique des Fluides, Thermique, Calcul de Structures et Interaction Fluide/Structure.

 

 

 

 

 

 

TABLE DES MATIERE

I       INTRODUCTION____________________________________________________ 4

II      POSITION DU PROBLEME____________________________________________ 5

II.1       Etude théorique________________________________________________ 5

II.2       Aérodynamique Automobile______________________________________ 5

II.3       Traînée aérodynamique globale___________________________________ 6

II.4       Formulation théorique___________________________________________ 6

II.5       Traînée visqueuse______________________________________________ 6

II.6       Coefficient local de frottement – Coefficient de traînée_________________ 6

II.7       Équations locales de couche limite dynamique iso volume______________ 7

II.8       Définition de la turbulence_______________________________________ 7

II.9       Modèles de turbulence__________________________________________ 8

III         RESOLUTION D’UN PROBLEME D’ECOULEMENT_________________________ 9

III.1      Création de la géométrie_________________________________________ 9

III.2      Maillage de la géométrie_________________________________________ 9

III.2.a      Importation de la géométrie___________________________________ 9

III.2.b      Préparation de la surface____________________________________ 10

III.2.c       Génération de la couche limite________________________________ 10

III.2.d      Génération de la finesse du maillage___________________________ 10

III.2.e      Création du maillage________________________________________ 11

III.2.f        Extrusion de la couche limite__________________________________ 11

III.2.g      Statistiques_______________________________________________ 11

III.2.h      Vérification du maillage______________________________________ 12

III.2.i        Correction du maillage______________________________________ 12

III.3      Modèle physique______________________________________________ 12

III.3.a      Création des conditions au limites_____________________________ 13

III.3.b      Type de modèle de turbulence________________________________ 13

III.3.c       Initialisation de la turbulence__________________________________ 13

III.3.d      Définition des vitesses d’entrées et/ou de sorties du fluide___________ 14

III.4      Vérification de l’ensemble du modèle______________________________ 14

III.5      Lancement du calcul___________________________________________ 14

III.6      Post-traitement_______________________________________________ 15

III.6.a      Chargement du fichier de résultat______________________________ 15

III.6.b      Chargement des données voulues_____________________________ 15

III.6.c       Affichage écran des données_________________________________ 15

III.6.d      Affichage du flux par particules________________________________ 16

IV        ANALYSE DES RESULTATS________________________________________ 16

IV.1     Géométries simples___________________________________________ 16

IV.1.a      Ecoulement autour d’une sphère______________________________ 16

IV.1.b      Ecoulement autour d’un cube_________________________________ 17

IV.2     Application à des géométries plus complexes_______________________ 17

IV.2.a      Camionnette simplifiée______________________________________ 18

IV.2.b      Voiture avec béquet simplifiée_________________________________ 19

V     CONCLUSION____________________________________________________ 22

 

I                INTRODUCTION

 

 

Depuis les années 70, de nombreux progrès ont été réalisés en aérodynamique automobile, et ceux grâce aux souffleries construites en France entre 1974 et 1985.

 

 

Aujourd’hui, il subsiste de nombreux défis à relever, pour que les véhicules soient adaptés aux attentes des consommateurs, tout en respectant les engagements environnementaux pris par les constructeurs.

 

Il y a donc trois principaux domaines nécessitant des recherches approfondies :

 

• La réduction de la traînée aérodynamique des véhicules, qui a en effet une influence notoire sur la consommation et de fait sur le taux de rejet de gaz carbonique dans l’atmosphère.

 

• La réduction des bruits aérodynamiques : l’acoustique dans les voitures est un des points majeurs à travailler lors de la phase de développement.

 

• La sécurité des véhicules : pour augmenter la sécurité des véhicules, il est nécessaire de travailler sur la stabilité dynamique du véhicule, en particulier sur l’influence des vents latéraux.

 

Le contrôle aérodynamique est un sujet d'une importance économique cruciale. Dans l'industrie automobile on assiste depuis quelques années à une stagnation dans l'amélioration des coefficients de pénétration par simple optimisation de forme. Les futures limitations de pollution obligent à se tourner vers des techniques de contrôle actif qui consistent à imaginer par exemple des injections de jets sur les parois.

L'analyse systématique de ces approches en est encore à son balbutiement, et on cherche pour l'instant surtout à comprendre les modifications de l'écoulement lorsqu'on bouge ou déforme l'obstacle. Ceci nécessite des codes robustes, rapides et précis permettant de faire des simulations tridimensionnelles utilisant plusieurs millions de points.

L'utilisation de la simulation numérique en mécanique des fluides est en pleine expansion dans l’industrie, et en particulier dans le domaine automobile.

Celle-ci consiste à modéliser les écoulements et les échanges de chaleurs pour un problème donné : elle permet donc à l’industriel de comprendre et de quantifier les phénomènes physiques sans avoir recours à des essais. Ainsi, la simulation réduit considérablement le prix des études lors de la conception d’un produit car elle contribue à diminuer le nombre d'essais expérimentaux (en soufflerie ou sur banc) et la construction de prototypes.

 

 

La simulation en mécanique des fluides est réalisée grâce à des logiciels tels que FLUENT, avec lesquels on obtient des cartographies tridimensionnelles de toutes les variables mises en jeu (vitesse, température, pression, etc.). A partir de ces données, les caractéristiques des phénomènes étudiés peuvent être calculées : efforts aux parois, flux thermiques, débits, pertes de charges, coefficients aérodynamiques, …

 

II              POSITION DU PROBLEME

 

 

 

On se propose dans cette étude la mise en évidence des écoulement autour d’un véhicule, et visualiser ainsi les conséquences et les effets résultants pour pouvoir en tirer les modifications qui s’imposent sur la conception de l’auto du point de vue du design et du profile.

 

 

II.1     Etude théorique

L'aérodynamique est une discipline qui considère des objets aux prises avec des écoulements. Comme telle, elle constitue un chapitre de la mécanique des fluides. Que ce fluide soit de l'air, c'est à dire un gaz, ou qu'il soit un liquide, ne change rien à la manière d'aborder les choses, et les lois qui s'appliquent aux fluides gazeux sont les mêmes que celles qui s'appliquent aux fluides liquides.

Une différence cependant distingue les liquides des gaz : ces derniers sont compressibles. La compressibilité apporte une complexification non négligeable au niveau des calculs alors que le phénomène physique reste parfaitement négligeable pour les vitesses qui nous préoccupent en aéronautique légère (vitesses inférieures à Mach 0.5 ou 0.6). C'est la raison pour laquelle on a pris l'habitude de différencier le supersonique du subsonique, ce dernier évitant une complexité inutile de la formulation mathématique. L'erreur entraînée par cette simplification est largement inférieure aux imprécisions du calcul.

 

Ce qu'il convient de souligner, c'est que l'aérodynamique est avant tout et par essence, une science expérimentale. On ne niera pas l'utilité de la théorie, car elle permet d'élaborer des modèles mathématiques simulant la réalité, ce qui est toujours une économie de temps, d'argent et d'énergie, et apporte une sécurité accrue. Mais un modèle et sa simulation doivent toujours faire appel à l'expérience pour trouver une confirmation par les faits, confirmation validant un champ forcément limité d'applications.

 

II.2     Aérodynamique Automobile

 

L’écoulement dans le sillage des véhicules automobiles peut-être séparé en deux structures. La première issue d’une ligne de séparation bidimensionnelle génère un écoulement de base avec une pression statique constante et une vitesse de transport voisine de zéro.

 

La seconde et issue d’une séparation tridimensionnelle de l’écoulement et engendre des zones à enroulements tourbillonnaires. Ces deux effets produisent la traînée de forme à laquelle s’ajoute une traînée de pression résultant de la distribution de pression sur la géométrie du véhicule et une traînée de frottement due au cisaillement du fluide dans la couche limite.

 

L’ensemble constitue la traînée aérodynamique globale associée au véhicule et son optimisation suppose que l’on puisse identifier les différentes grandeurs physiques qui la caractérisent.

 

 

II.3     Traînée aérodynamique globale

 

En aérodynamique automobile, les écoulements fluides sont de nature turbulente et dans les conditions courantes d’utilisation, le déplacement du véhicule s’effectue à un nombre de Mach très inférieur à 0.3.

 

De plus, les actions mécaniques de gravité que le fluide exerce sur le véhicule sont faibles comparées aux actions mécaniques de viscosité, de turbulence ou de pression. Pour ces raisons le fluide est considéré incompressible et non pesant.

 

Pour analyser la traînée aérodynamique sous l’aspect tourbillonnaire on va s’intéresser à une formulation intégrale construite sur un bilan de quantité de mouvement à partir des pressions moyennées au sens de la turbulence.

 

II.4     Formulation théorique

 

1^er terme : Contribution due à la vitesse longitudinale

2^ème terme   : Contribution due à la rotation du fluide

3^ème terme  : Contribution due à la perte de pression d’arrêt

 

 

 

 

 

 

II.5     Traînée visqueuse

 

Par intégration du frottement pariétal sur toute la surface mouillée de l’obstacle, on obtient la traînée visqueuse par unité d’envergure en écoulement 2D plan :

 

 

II.6     Coefficient local de frottement – Coefficient de traînée

Le coefficient local de frottement est défini à partir de la contrainte pariétale locale normée par la pression dynamique soit : 

 

 

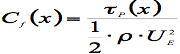Le coefficient de traînée s’obtient de façon similaire à partir d’une surface de référence et d’une pression dynamique.

 

Elle est définie à partir de la vitesse à l’infinie :

 

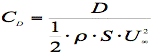
II.7     Équations locales de couche limite dynamique iso volume

 

Dans le cas 2D plan en absence de forces extérieures volumiques les équations générales de Navier-Stokes s’écrivent : 

 

 

II.8     Définition de la turbulence

 

Définition : mouvement non stationnaire, non périodique dans lequel les trois composantes de vitesse fluctuent.

 

La turbulence est un mode naturel d’écoulement d’un fluide visqueux où des mécanismes internes d’échange d’énergie assurent la création et le maintien de toute une hiérarchie de mouvements chaotiques répartis continûment sur une large gamme d’échelle macroscopiques. 

 

La vitesse est donc décomposée en une moyenne et une partie fluctuante:

 

 

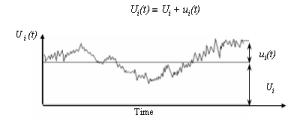
Fluctuations similaires pour la pression, la température, la concentration

 

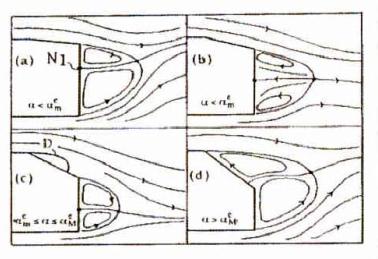
Exemple de schéma de turbulence

 

Modélisation de la turbulence sur une surface simplifiée

 

 

II.9     Modèles de turbulence 

 

Les équations principales, qui gouvernent les 3 modèles de turbulence (DNS, LES, RANS) sont :

 

 

 

 

Afin de modéliser l’ensemble de ces phénomènes, on utilise donc le logiciel Star-CD.

 

Le prochain chapitre détaillera donc les principales étapes de création d’un modèle pour ce logiciel et de résolution d’un problème.

 

 

 

 

 

III            RESOLUTION D’UN PROBLEME D’ECOULEMENT

 

 

L’utilisation de Star-CD est complexe. Celle-ci se fait par utilisation de plusieurs modules spécifiques.

 

N’ayant pas accès au modeleur de Star-CD, on doit donc créer la géométrie par un autre logiciel, et utiliser un format d’enregistrement compatible.

 

 

III.1   Création de la géométrie

 

 

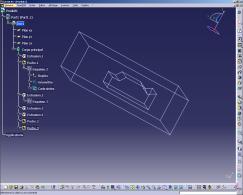
On utilise donc Catia V5R8 afin de créer la zone ou le fluide va s’écouler.

 

On peut en particulier créer la « boite » en tant que corps de pièce principale et la forme que l’on va supprimer en corps de pièce normal.

 

On applique enfin l’opération booléenne retirer et on obtient donc une géométrie, à enregistrer au format stl.

 

 

 

On utilise donc dans l’ensemble des calculs, afin de mailler notre géométrie, le mesh wizard de Pro-Am.

 

III.2   Maillage de la géométrie

 

III.2.a     Importation de la géométrie

 

 

 

 

 

 

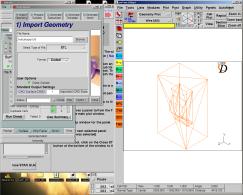
Dans cette étape, on va simplement chercher par « Browse » le fichier stl créé par Catia, afin de le stocker en mémoire.

 

 

 

 

 

 

 

 

 

III.2.b     Préparation de la surface

 

 

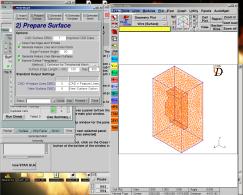
Dans cette étape, Star-CD va préparer la surface afin de faciliter le maillage.

 

On va donc choisir des tailles maximales et minimales de surfaces que Star-CD va utiliser pour « mailler » la surface, ou plutôt pour la préparer au maillage.

 

Dans cette étape, on supprime donc de la géométrie tous les détails inférieur la taille minimale choisie.

 

 

 

III.2.c     Génération de la couche limite

 

 

 

 

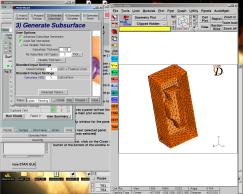
On va choisir ici l’épaisseur de la couche limite, qui sera maillé indépendamment par extrusion du maillage de surface sur une maille, et qui est donc enlever du modèle courant pour les deux étapes suivantes.

 

 

 

 

 

 

III.2.d     Génération de la finesse du maillage

 

 

 

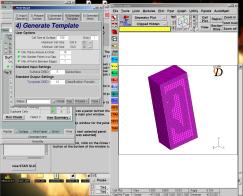
On choisit ici des valeurs maximales et minimales entre lesquelles le mailleur automatique va gérer la finesse du maillage.

 

On obtient donc à la fin de cette étape une cartographie pour l’ensemble de la structure de la finesse du maillage qui sera utilisée dans l’étape suivante.

 

 

III.2.e     Création du maillage

 

 

 

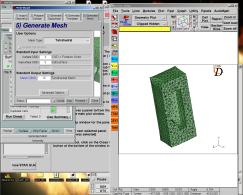
Dans cette étape, à partir de la cartographie de finesse du maillage, le mailleur va mailler le volume par des mailles de type tétraédrique ( tetrahedral ) ou cubique ( trimmed ) au choix de l’utilisateur.

 

 

 

 

 

 

III.2.f       Extrusion de la couche limite

 

 

 

 

 

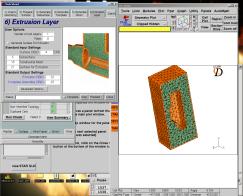
Ici, le mailleur va reconstituer la couche limite par extrusion du maillage de surface, afin d’obtenir des mailles d’épaisseurs égales à l’épaisseur de la couche limite.

 

 

 

 

 

 

III.2.g     Statistiques

 

 

 

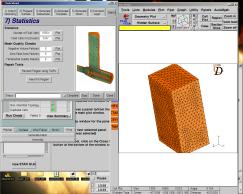
On vérifie ici l’ensemble des paramètres générés par le mailleur automatique, c’est à dire le nombre de mailles de fluide, le nombre de mailles générées par l’extrusion lors de l’étape précédente, ainsi que le nombre de mailles « ratés ».

 

 

 

 

 

 

 

 

III.2.h     Vérification du maillage

 

 

 

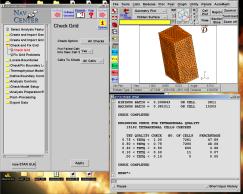
Le mailleur automatique n’étant pas parfait, il est nécessaire de vérifier le maillage obtenu par le Star-Guide.

 

On utilise donc le « check grid », avec comme option de vérification : « severe check ». On obtient alors un listing des vérifications dans la fenêtre texte de Pro-Am.

 

 

 

 

 

III.2.i       Correction du maillage

 

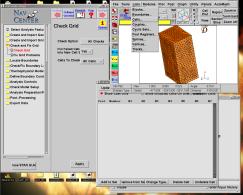
Maintenant que le maillage est vérifié, il convient de supprimer les mailles défectueuses. Pour cela, on va lister celles-ci par le menu « lists », et « cells ». Une fenêtre s’affiche, listant l’ensemble des mailles défectueuses. On les supprime donc, et on fait de même pour les couples.

Mais cette opération peut créer de nouveaux problèmes dans le maillage. On doit donc itérer les opérations 9 et 10 jusqu’à l’obtention d’une fenêtre vide dans les deux listing.

 

 

 

 

III.3   Modèle physique

 

Dans cette étape, on va renseigner l’ensemble des caractéristiques physique du fluide, ainsi que des parois.

 

On ne modifie qu’une petite partie de ces caractéristiques, car, par exemple, le fluide par défaut est de l’air, qui convient donc parfaitement à notre étude.

 

 

 

 

 

 

 

III.3.a     Création des conditions au limites

 

 

 

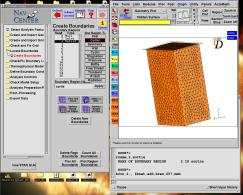
Toujours dans le Star-Guide, on va identifier les zones d’entrée et de sortie du fluide, dans « Locate Boundaries ».

 

On choisira la méthode « Select a zone », qui semble après utilisation des différentes méthodes la plus efficiente.

 

 

 

 

 

 

III.3.b     Type de modèle de turbulence

 

 

 

 

 

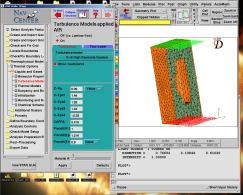
On choisis donc ici le type de modèle de turbulence ainsi que les valeurs de paramètres associés.

 

 

 

 

 

 

 

 

III.3.c     Initialisation de la turbulence

 

 

 

 

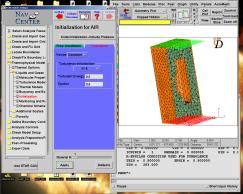
La turbulence ne se créant pas spontanément dans les modèles, on doit l’initialiser en début de calcul. Ceci est fait en donnant une énergie turbulente et un epsilon différents de 0, ici 0,5.

 

 

 

 

 

 

 

III.3.d     Définition des vitesses d’entrées et/ou de sorties du fluide

 

 

 

 

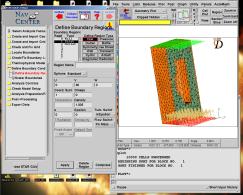
On donne ici les caractéristiques de toutes les conditions initiales ( entrées, sorties, murs ). Dans notre cas, on ne rentre qu’une vitesse d’entrée du fluide, selon l’axe Y.

 

 

 

 

 

 

III.4   Vérification de l’ensemble du modèle

 

 

 

 

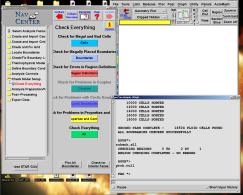
Comme indiqué dans le titre, on vérifie ici l’ensemble des paramètres du modèle, la lecture des vérifications se faisant dans la fenêtre texte.

 

 

 

 

 

 

 

III.5   Lancement du calcul

 

 

 

 

 

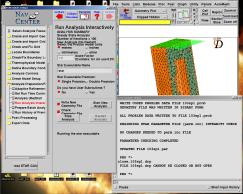
Après vérification du modèle et des conditions aux limites, on lance enfin le calcul dans cette fenêtre, avec la bonne unité.

 

 

 

 

 

 

 

III.6   Post-traitement

 

III.6.a     Chargement du fichier de résultat

 

 

 

 

 

Les résultats sont stockés dans un fichier spécial, il convient donc de le charger en mémoire.

 

 

 

 

 

 

 

III.6.b     Chargement des données voulues

 

 

 

 

 

Dans cette étape, on charge pour l’affichage en vecteur et en couleur les données voulues du fichier résultat.

 

 

 

 

 

 

 

III.6.c     Affichage écran des données

 

 

 

 

 

A partir des données chargées à l’étape précédente, on les affiche à l’écran, avec la visualisation voulue.

 

 

 

 

 

 

III.6.d     Affichage du flux par particules

 

 

 

On peut aussi, à partir du fichier résultat, obtenir une visualisation du flux par insertion de particule sans masse, et en visualisant leur parcours. Nous ne développerons pas cette méthode, n’étant pas le but de ce projet.

 

 

 

 

 

 

Cette présentation des étapes de résolution n’est bien sur pas complète, mais elle présente les grandes étapes pour la résolution des problèmes d’écoulement pur.

 

IV           ANALYSE DES RESULTATS

 

Notre étude nous a amené à effectuer plusieurs tests et simulations sur différents modèles avec différents maillages pour une meilleure familiarisation avec le logiciel.

Dans un premier temps, nous avons effectuer des calculs sur des géométries basiques afin d’obtenir « facilement » des résultats.

 

IV.1  Géométries simples

 

IV.1.a    Ecoulement autour d’une sphère

Dans un premier temps, nous avons utilisé comme géométrie une sphère, qui nous semblait une géométrie propice à une analyse de résultat aisée. Nous avons donc mailler le modèle avec des élément « trimmed », et avec une vitesse d’entrée du fluide élevé. ( 70 m.s^-1)

Nous avons donc obtenu le résultat suivant :

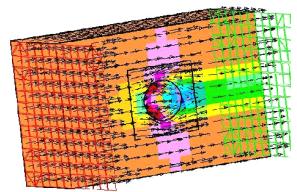
On peut voir que les lignes de courant épousent bien la forme de la sphère. On constate bien les point d’arrêts à l’avant de la boule, et la carte de couleurs nous donnant la distribution de la pression autour de l’obstacle est bien conforme à ce qui était attendu.

La vitesse d’écoulement augmente bien autour de la sphère, ce qui était aussi attendu.

On peut donc dire que le modèle répond bien au attente.

 

IV.1.b    Ecoulement autour d’un cube

 

Dans un deuxième temps, et afin d’obtenir une traînée plus complexe, nous avons choisi d’utiliser un cube, toujours mailler en « Trimmed », avec la même vitesse en entrée que précédemment.

 

Nous avons alors obtenu le résultat suivant :

 

 

 

 

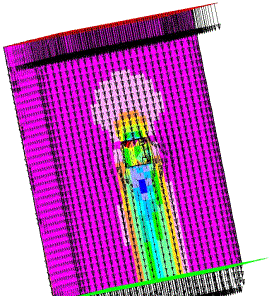
On constate bien les nombreux points d’arrêts à l’avant du cube, et la carte de couleurs nous donne la distribution de la pression autour de l’obstacle qui diminue derrière ce dernier.

 

Les lignes de courants sont comme prévu horizontales, sauf derrière le cube à cause de la dépression.

 

Dans ce cas, aucun modèle de turbulence n’a été utilisé, et donc aucune turbulence ne peut être visible à l’arrière du cube.

 

 

 

 

 

 

 

IV.2  Application à des géométries plus complexes

 

Après avoir effectué et vérifié la validité des deux calculs précédents, nous avons tenter de nous rapprocher de l’aérodynamique automobile en entrant comme modèle des voitures simplifier, mais de dimensions se rapprochant de la réalité.

 

Dans l’ensemble des calculs sur voitures, nous avons utilisé une vitesse d’entrée pour le fluide de 30 m.s^-1, c’est à dire 107 km.h^-1, ce qui est une vitesse réaliste pour les simulations. Le modèle de turbulence utilisé fut le modèle k-e avec grand nombre de Reynolds.

 

Le premier modèle utilisé fut celui d’une camionnette simplifiée.

 

 

IV.2.a    Camionnette simplifiée

 

 

Dans un premier temps, et pour faciliter l’obtention de résultats, nous avons choisi de mailler grossièrement le modèle avec des mailles hexaédriques.

 

Nous avons obtenu les résultats suivant :

 

 

 

 

 

 

 

 

 

 

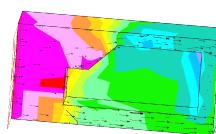
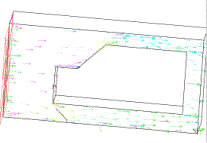
Il est clair que les résultats, étant donné le maillage, ne peuvent être concluant. Nous avons donc choisi de remailler la structure avec un maillage plus fin.

 

 

 

 

 

 

 

 

 

 

 

 

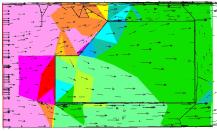
Les résultats n’étant toujours pas satisfaisant, on va donc prendre un maillage « trimmed », et raffiner encore le maillage.

 

 

 

 

 

 

 

 

 

 

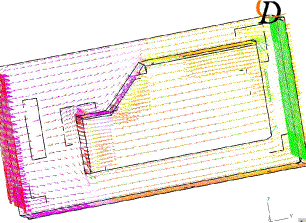
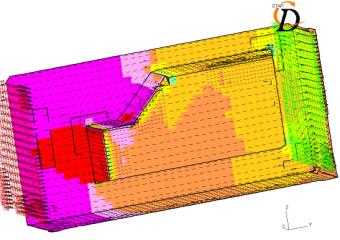
Les résultats semblent enfin satisfaisant en ce qui concerne l’écoulement et la pression à l’avant et autour de la camionnette. Par contre, n’ayant pas laissé de place derrière la camionnette, il n’est pas possible de distinguer les turbulences qui devraient se créer à ce niveau.

 

Ce problème sera donc en partie réglé dans le prochain modèle.

 

IV.2.b    Voiture avec béquet simplifiée

 

Un premier maillage du modèle fut effectué, dont les résultats pour l’ écoulement et pour la pression semblaient concluants, mais les turbulences à l’arrière du modèle n’étaient pas celles attendues.

 

 

 

 

 

 

 

 

 

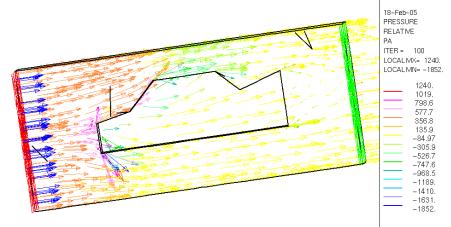
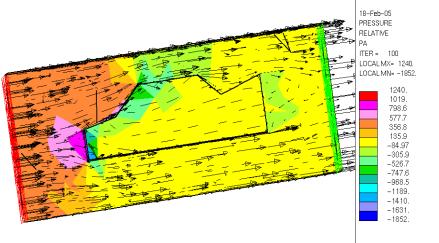
Nous avons donc alors raffiné le maillage, et obtenu les résultats suivants :

 

 

 

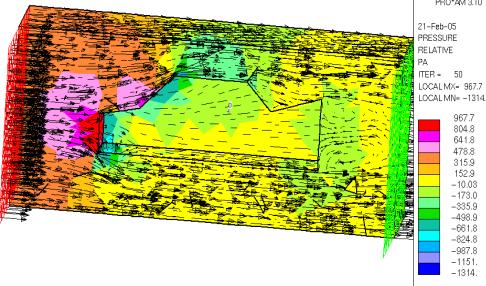
Cartographie de la pression relative et des vecteurs vitesses du fluides

Vortex de turbulences

 

 

 

 

 

 

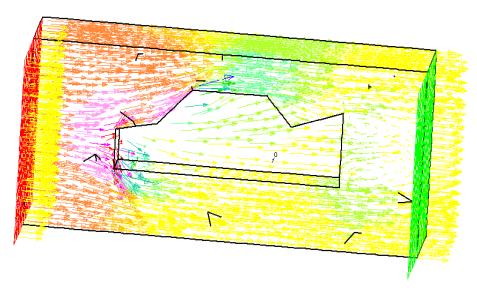
Enfin, pourrait on dire, le modèle et les résultats obtenus sont pleinement satisfaisant. L’écoulement est réaliste, les points d’arrêts sont bien présents, mais surtout, la turbulence ressemble bien à la réalité ( cf Chap. II.9 ).

 

Ce résultat est de loin le meilleur sur tous les points que nous avons obtenu. Afin de mieux visualiser l’écoulement, on utilise le calcul et l’affichage d’une flux de particules sans masse.

On obtient alors une animation, rendant compte de la trajectoire des 10 particules dans le modèle. Le résultat final est le suivant :

 

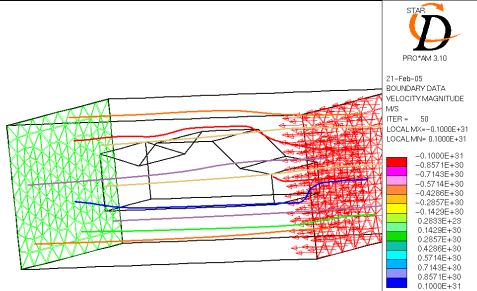
V             CONCLUSION

 

 

Cette étude nous a amené dans un premier temps à effectuer des recherche sur l’aérodynamique en générale et sur son application à l’automobile d’une manière particulière. Une voiture qui roule dans un fluide (air), est soumise à des forces (résistance de l'air, poids, frottements, …), réparties en surface (sCx), dont les valeurs et distributions dépendent du fluide, de son état physique (gazeux), de la vitesse relative, et bien sûr de la forme du corps (Cx) et de la rugosité de sa surface. La somme de ces forces peut être décomposée en une composante dirigée en sens inverse de la vitesse, appelée résistance ou traînée, et une composante perpendiculaire appelée portance en aérodynamique.

 

Dans un deuxième temps, le projet nous a amené à se familiariser avec le logiciel Star- CD, qui est l’un des logiciels les plus performants existant sur le marche actuellement dans le domaine de la mécanique des fluides, et ainsi pouvoir mettre en évidence par simulation les phénomènes aérodynamiques, étudié théoriquement.

 

Notre rapport a donc pour objectif de faciliter la prise en main du logiciel Star-CD pour les futurs étudiants.

 

N’ayant pas eu de documentations efficaces à notre disposition, notre souci a été de bien détailler les étapes à suivre pour mener à bien une simulation.

 

Le calcul du C_x d’une voiture n’a donc pas été possible, en raison de problèmes de temps et de logiciel.