![]() Olivier ANSART
Olivier ANSART
Fabien AVRILLAS
Eric KREMER
Ibrahima NIANG
Karim ZANNIR

 MNRV 2
MNRV 2
Projet scolaire
2004/2005
![]() Olivier ANSART
Olivier ANSART
Fabien AVRILLAS
Eric KREMER
Ibrahima NIANG
Karim ZANNIR

 MNRV 2
MNRV 2
Projet scolaire
2004/2005
Mots clés :
Abaqus
Prise en main
Crash
Eléments finis
Simulation Numérique
I. Introduction.................................................................................. 1
II. Historique du crash test voiture.................................................... 3
III. Prise en main d’Abaqus 6-4-1....................................................... 7
IV. Import CAO /calcul...................................................................... 36
V. Apprentissage par exercices....................................................... 38
VI. Crash voiture.............................................................................. 47
VII. Conclusion.................................................................................. 48
L’avenir est à l’outil numérique et à la réalité virtuelle; la simulation et l’analyse numérique se sont développées ces dernières années dans la recherche industrielle privée ou publique (constructeurs automobile, aéronautique, spatial…) améliorant ainsi la productivité des industriels et la vie de tous les consommateurs.
La solution d'analyse par éléments finis optimise le prototypage virtuel et la simulation numérique pour l'entreprise en utilisant les hypothèses de la mécanique de la rupture en élasticité et de la dynamique. Ainsi elle simule et améliore les performances des composants, des matériaux et des produits sujets à de fortes exigences opérationnelles (sécurité, endommagement…).
La simulation et l’analyse numérique ont un impact direct sur la qualité et le temps de mise sur le marché des produits ; de plus, elles accroissent les performances des solutions de gestion du cycle de vie du produit.
Elles sont apparues, dans le désire de minimiser le coût d’une étude avec un nombre d’essais optimisés. La difficulté est de créer un modèle C.A.O. se rapprochant au maximum de la réalité (matériaux, conditions aux limites…). L’étude ne sera validée qu’à partir d’essais physiques entraînant des mesures pour la comparaison entre la réalité et la simulation (crash test…).
D’un point de vue technique, les résultats obtenus grâce à ABAQUS sont le bilan des énergies, des forces nodales, des déformations, des déplacements, des contraintes, des vitesses, des accélérations et de toutes les grandeurs physiques nécessaires à la conception d’un modèle.
Les logiciels de calcul de structures comme NASTRAN, RADIOS, ANSYS sont utilisés pour la modélisation de l’endommagement d’une structure métallique. Nous utiliserons le logiciel ABAQUS (analyse dynamique linéaire et non linéaire).
· Problématique :
Le but de notre projet est la conception d’un modèle de crash de voiture :
-Le dimensionnement des structures
-Le choix du matériau approprié pour notre étude
-L’étude des contraintes à partir de l’endommagement
Cela passera par la prise en main du logiciel par le biais d’exercices simples.
· A propos d'ABAQUS :
Fondé en 1978, ABAQUS, est l'un des premiers fournisseurs mondiaux de logiciels et services pour l'analyse par éléments finis. La gamme de logiciels d'ABAQUS est particulièrement réputée pour sa technologie, sa qualité et sa fiabilité. Elle s'est imposée comme partie intégrante des processus de conception de sociétés de renommées mondiale dans tous les secteurs industriels. ABAQUS offre les meilleures solutions pour des problèmes linéaires, non linéaires, explicites et dynamiques. Le logiciel fournit un environnement inégalé pour l'analyse par éléments finis, proposant un grand nombre d'alternatives aux opérations impliquant des fournisseurs et des produits multiples. ABAQUS, c'est une structure de plus de 350 personnes, 24 agences implantées dans le monde et un réseau de distributeurs sur les marchés émergents. Pour en savoir plus : (www.abaqus.com).
Le crash test est la phase de validation du modèle numérique (cohérence entre les résultats théoriques et les résultats expérimentaux).
II. Historique du crash test voiture
· Le crash test Européen (l’euro NCAP : « front collision star rating »)
Préambule:
La méthode des crash tests employés par l’euro NCAP est assez complexe : préalablement, l’euro NCAP achète en Europe des voitures de grandes diffusions, anonymement. Puis, suivant le type de choc elle applique différentes méthodes.
Le fait que les tests se fassent avec une voiture de type anglaise (volant à droite) ne change rien, car l'architecture de la voiture est strictement symétrique ...
Le choc frontal :
Les voitures sont projetées à 64 km/h (La
directive européenne prévoit "uniquement" 56 km/h) contre une
barrière métallique déformable. 40% de la voiture uniquement (coté conducteur)
heurte la barrière. C’est pour cela que la voiture se déporte vers la droite,
après le choc.
Pour ce choc, on installe deux mannequins bardés de capteurs, mesurant les contraintes, déformations, et chocs des principaux organes du corps.
Ensuite, les ingénieurs de l’euro NCAP mesurent et évaluent l’efficacité des airbags, du déplacement du volant, des déchirures du plancher, et bien sur des contraintes exercées sur les mannequins.
De plus, l’euro NCAP installe aussi des mannequins enfants (représentant des enfants âgés de 18 mois et trois ans) dans des sièges autos préconisés par le constructeur et mesure là aussi les contraintes exercées sur les enfants. Mais ces tests n’affectent pas la note obtenue par une voiture.
|
|
Le choc latéral :
Un chariot ou "bélier" (avec structure déformable) lancé à 50 km/h heurte l’automobile coté conducteur (même vitesse que la directive européenne).
Pour ce choc, on installe uniquement un mannequin coté conducteur, bardés de capteurs, mesurant les contraintes, déformations, et chocs des principaux organes du corps (du bassin à la tête).
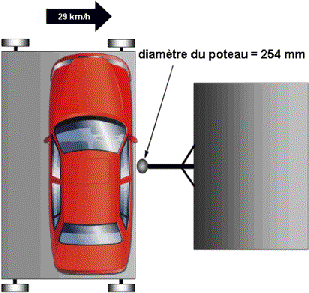
Le test du poteau :
Le test du poteau fut introduit par l'euro NCAP au
début de l'année 2000. Il permet à une voiture de gagner 2 points en plus, et
donc, si les autres tests sont satisfaisants d'obtenir la nouvelle note
maximale : 5 étoiles.
Ce test a été mis en place pour tester la protection apportée par les airbags de type "rideau" sur la tête du conducteur : On lance la voiture a 29 km/h (sur une plate-forme) contre un poteau de diamètre 25,4 cm, fixe, censé représenter un arbre par exemple ou un poteau électrique. Pour réaliser ce test, la voiture doit préalablement obtenir une tête verte au choc latéral, puis que le constructeur demande à l'euro NCAP de réaliser ce test sur cette voiture.
![]() Après mesure des pressions
exercées sur la tête du conducteur, l'euro NCAP donne à la voiture, en cas de
succès, 2 points supplémentaires, c'est à dire, que maintenant, le test latéral
est noté sur 18, et que la note globale est sur 34.
Après mesure des pressions
exercées sur la tête du conducteur, l'euro NCAP donne à la voiture, en cas de
succès, 2 points supplémentaires, c'est à dire, que maintenant, le test latéral
est noté sur 18, et que la note globale est sur 34.
Le choc contre piéton :
Ce choc ne compte pas dans le total des points et donc sur le nombre d'étoiles.
La voiture heurte à 40 km/h un mannequin représentant un adulte de face, ainsi
qu’un enfant.
Pour ce choc, on étudie les points d’impact et la force de l’impact sur les mannequins et sur la voiture. On note de la même manière que pour les autres chocs, mais ici, avec des étoiles bleues.

La notation :
Pour chaque choc (frontal et latéral), on représente les résultats par une couleur sur chaque partie du corps, symbolisant le niveau de protection des passagers. La synthèse de ces deux résultats (16 points + 16 points et 2 points "bonus" possible) est représentée par des étoiles jaunes : Plus la voiture en obtient, plus elle est "sûr".
En outre, une étoile barré signifie que la voiture mériterait (en résultat brute) d’obtenir cette étoile, mais la structure de la voiture, et donc les risques pour les passagers, sont trop importants pour l’obtenir. Il en est de même avec les piétons, leur protection est représentée par des étoiles bleues, suivant le niveau de protection obtenue. De plus, il est a noter que la note du choc frontal n'est basée que sur les performances du conducteur sauf si le passager est moins bien protégé.
|
|
||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||
Le marché mondial exige que les véhicules satisfassent également aux normes du crash test propre à chaque continent. Le véhicule sera ainsi homologué pour le marché souhaité.
III. Prise en main d’Abaqus 6-4-1
· Description du logiciel :
Le logiciel est divisé en neuf modules indépendants les uns des autres :
-Part ;
-Property ;
-Assembly ;
-Step ;
-Interaction ;
-Load ;
-Mesh ;
-Job ;
-Visualisation ;
-Sketch.
Parmi les méthodes d’analyse dynamique on trouve notamment Abaqus standard et explicite.
-Abaqus/Explicit
La version explicite est entièrement vectorisée afin d'utiliser les supercalculateurs multiprocesseurs. Bien que l'analyse soit dynamique, elle peut être utilisée moyennant quelques précautions pour accomplir des analyses quasi-statiques. Le schéma explicite implanté au sein d’Abaqus conduit à des temps de calcul plus faibles comparativement au schéma implicite nommé ABAQUS/Standard. L'algorithme explicite assure une certaine robustesse, il est plus efficace pour aboutir à un calcul complet que Abaqus/Standard. Ce code présente une bonne résolution des contacts ce qui est un autre intérêt vis-à-vis de la simulation du procédé. ABAQUS/Explicit met en oeuvre un schéma d'intégration par différences centrales exprimé par les équations (1.1) et (1.2).
|
du(i+1/2)/dt = du(i-1/2)/dt + [ (Dt(i+1) +Dt(i)) / 2 ] * d²u(i)/dt² |
(1.1) |
|
u(i+1) = u(i) + [ (Dt(i+1) * du(i+1/2)/dt] |
(1.2) |
où du/dt est la vitesse et d²u/dt² est l'accélération. L'exposant (i) indique le numéro de l'incrément.
Ces équations sont illustrées sur la figure 1.3. :
|
|
|
Figure 1.3: Illustration de l'opérateur de différence centrale |
Ce seul schéma d'intégration est combiné à une procédure dynamique. La clef de l'efficacité calculatoire de la procédure explicite provient de l'utilisation d'une matrice de masse diagonale. Une telle forme permet un calcul rapide de l'inverse de cette matrice notamment utilisée pour la détermination de l'accélération de l'équation (1.4).
|
d²u(i)/dt² = M^(-1) * ( F(i) – I(i) ) , |
(1.4) |
où M est la matrice de masse diagonale, F est le vecteur des charges appliquées et I
est le vecteur des forces internes. Ainsi, la procédure explicite ne requiert
ni itération ni matrice tangente de rigidité. La procédure explicite intègre
par rapport au temps en utilisant beaucoup de petits incréments de temps. Or,
l'opérateur de différences centrales est conditionnellement stable. La limite
de cette stabilité pour cet opérateur est donnée en terme de plus grande valeur
propre du système par :
![]()
Une estimation de la plus petite valeur propre du système peut être obtenue en déterminant le mode maximum des éléments du maillage. Ainsi, l'incrément de temps permettant la stabilité est donnée par :
Dt = min ( Le/Cd )
où Le est la dimension caractéristique des éléments et Cd est la vitesse des ondes en dilatation dans le matériau. Cette vitesse est donnée par :
Cd= √[(l+m)/r]
l= K-(2/3) * m
avec :
![]()
DS= 2 * m * Dρ
l= K - (2/3) * m
Le tenseur S est le tenseur des contraintes déviatoires et ρ est le tenseur des déformations déviatoires. r est la masse volumique du matériau. Ainsi, la procédure explicite dynamique peut effectuer un grand nombre de petits incréments pour un temps de calcul raisonnable.
-Abaqus/Standard :
Généralement, c'est la méthode de Newton qui est utilisée pour résoudre les problèmes non linéaires. La base du formalisme de cette méthode est la suivante. Considérons qu'après i itérations sur l'incrément de temps, l'approximation de la solution est u(i). La différence entre la solution exacte et la solution après i itérations est notée c(i+1). La solution exacte est donc donnée par :
u= u(i) + c(i+1)
En écrivant symboliquement le principe des travaux virtuels par une équation implicite,
F(u)= 0.
cela signifie l'équilibre par rapport à la variable nodale considérée. Cette équation implicite peut être développée en série de Taylor en u(i), ce qui donne :
|
F[u(i)] + (¶F[u(i)]/¶u(i)) * c(i+1) + (¶²F[u(i)]/¶u(i)) * c²(i+1) + ... = 0 |
(1.5) |
Si l'approximation est proche de la solution u(i), alors c(i+1). est petit et l'équation (1.5) peut être réduite à ces deux premiers termes donnant ainsi :
|
(¶F[u(i)]/¶u(i)) * c(i+1) =- F[u(i)] |
(1.6) |
Cette équation (1.6) permet de déterminer c(i+1) pour calculer l'approximation suivante u(i+1) par :
|
|
|
Figure 1.7: Illustration de la méthode de Newton |
La figure 1.7 illustre la méthode de Newton dont le but est de déterminer u tel que F(u)= 0.
Sur cette figure, on observe que la valeur nodale de l'incrément suivant utilise la matrice jacobienne comme une pente, en partant de la valeur courante. La convergence de cette méthode est quadratique, donc rapide.
Cependant, la matrice jacobienne (¶F[u(i)]/¶u(i)) peut présenter des problèmes d'existence et de singularité. Auquel cas, l'équation (1.6) est insoluble.
Premier module : Part
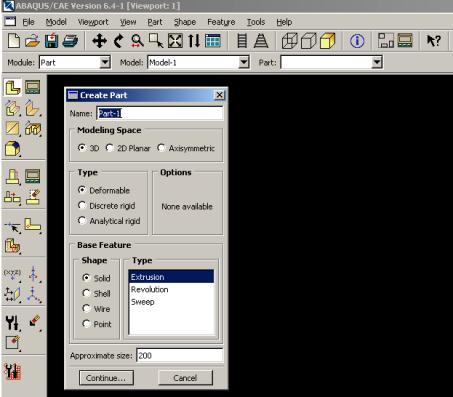
Dans cette première étape, l’utilisateur dessine toutes les pièces du problème. Chaque pièce est créée grâce à l’outil ‘Create Part’. Elles sont définies en fonction de leur nom (par défaut, le logiciel utilise le mot Part suivi d’un numéro, correspondant au nombre de pièces). Il faut ensuite entrer d’autres caractéristiques importantes.
Par exemple, il est nécessaire d’indiquer notre zone de travail : ‘3D’, ’2D planar’, si le problème se simplifie suffisamment pour être traité comme plan; ‘Axisymmetric’, utile dans le cas de la représentation simplifiée du modèle. Ces deux derniers points sont utilisés dans une perspective de simplification du problème, et, par conséquent de diminution du temps de calcul. Il faut aussi déterminer son ‘Type’ :‘Deformable’, ‘Discrete Rigid’ ou ‘Analytical rigid’, la pièce est définie soit comme déformable ou indéformable; et ses caractéristiques mécaniques qui sont au nombre de quatre: ‘Solid’, ‘Shell’, en français « coque » utilisé de préférence en ‘2D planar’, ‘Wire’ et ‘Point’. Tous les dessins élaborés sont bidimensionnelles, pour se rapporter dans l’espace de travail, en ‘3D’, il suffit de stipuler que sa construction se fait soit par ‘Revolution’, soit par ‘Extrusion’, ou ‘Sweep’, ces outils sont là pour créer une épaisseur.
 D’autres outils permettent d’améliorer le dessin en rajoutant des
détails de plus en plus minutieux, comme les outils d’affinage des arêtes par
implantation de congés, etc. Des modèles extérieurs peuvent être importés. Les
pièces peuvent être, à tout moment, modifiées grâce à l’outil ‘Feature Manager’, en
rajoutant, par exemple, ses dimensions afin de les modifier ensuite, nous
pouvons créer autant de modèle pour obtenir différents résultats numériques.
D’autres outils permettent d’améliorer le dessin en rajoutant des
détails de plus en plus minutieux, comme les outils d’affinage des arêtes par
implantation de congés, etc. Des modèles extérieurs peuvent être importés. Les
pièces peuvent être, à tout moment, modifiées grâce à l’outil ‘Feature Manager’, en
rajoutant, par exemple, ses dimensions afin de les modifier ensuite, nous
pouvons créer autant de modèle pour obtenir différents résultats numériques.
Deuxième module : Property.
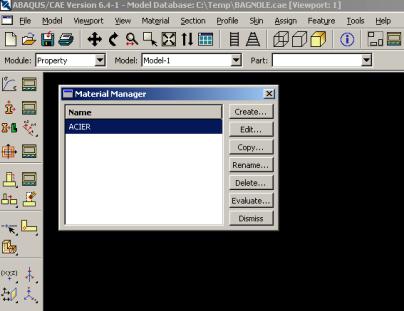
Ce module est important dans la modélisation numérique du phénomène physique. Il faut créer le matériau, c’est-à-dire, élaborer toutes ses propriétés mécaniques, thermiques ou acoustiques.
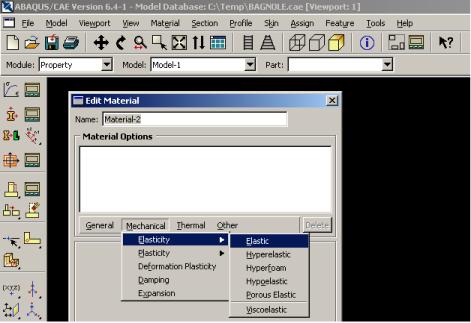
Dans la partie ‘Material Manager’, nous avons la possibilité de rentrer différentes valeurs numériques ou lois physiques. Le logiciel Abaqus travaille sans unités, il est donc préférable de les définir avant et de s’en tenir tout au long du calcul.
Tableau de correspondance des unités :
|
Masse |
Longueur |
Temps |
Force |
Pression |
Energie |
|
M |
L |
T |
M.L.T-2 |
M.L-1.T-2 |
M.L2.T-2 |
|
Kilogramme |
mètre |
seconde |
Newton |
Pascal |
Joule |
|
gramme |
millimètre |
milliseconde |
Newton |
MegaPascal |
milliJoule |
|
Tonne |
millimètre |
seconde |
Newton |
MegaPascal |
milliJoule |
Nous nous sommes restreints simplement aux problèmes mécaniques, dits de contact « instantané », plus précisément, le processus physique étudié est adiabatique (∆Q=0). Les propriétés thermiques ou acoustiques n’ont pas été définies. Nous n’avons pas utilisé les deux dernières sections, connues sous le nom de ‘Thermal’ et ‘Other’
Troisième module : Assembly
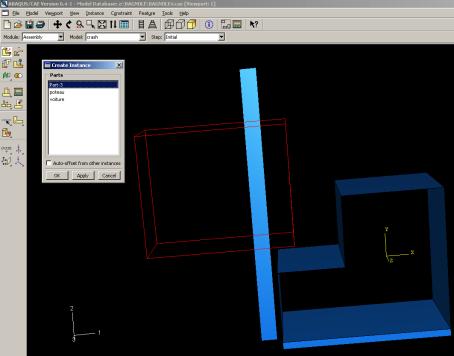
L’utilisateur rassemble toutes les pièces avec ‘Create Instance’ afin de modéliser le phénomène physique.
Le contact est réalisé avec ‘Create Constraint’ :
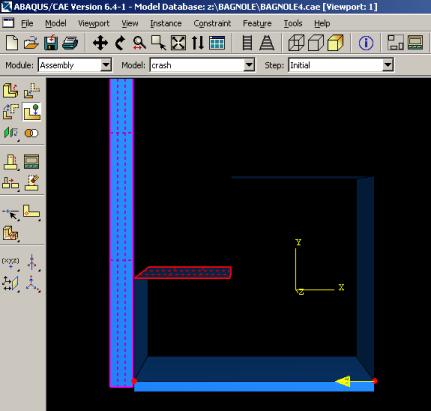
Il est crucial pour déterminer le contact entre deux pièces de définir les surfaces de contact, sa direction et la distance, ou ‘Clearance’, qui les séparent. Il faut déterminer une distance adéquate, éviter de trop les éloigner, pour optimiser la résolution : il faut éviter de demander au logiciel trop de calculs inutiles.
Quatrième module : Step
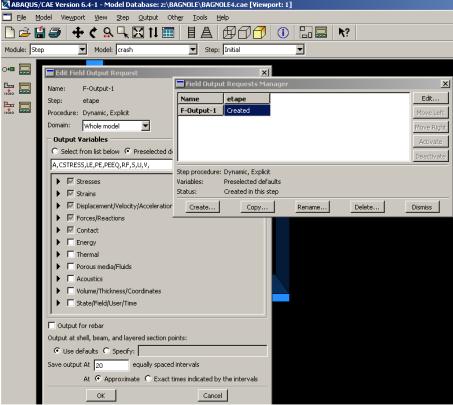
L’utilisateur définit tous les critères de calcul utilisés par Abaqus dans le module Job. En particulier il détermine l’incrémentation, valeur du pas de temps, et la valeur du temps final, qui est un temps « virtuel », temps sans unité. Le temps réel ou physique est défini en fonction des unités (cf.tableau dans ‘Material Manager’).
Il faut définir les variables de sortie utiles dans le module de ‘Visualisation’
 Cinquième module : Interaction
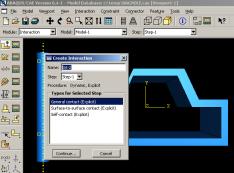
Cinquième module : Interaction
Il définit les interactions entre chaque pièce et introduit les premières hypothèses portant sur les contacts, les contraintes et les connections éventuelles.
Sixième module : Load
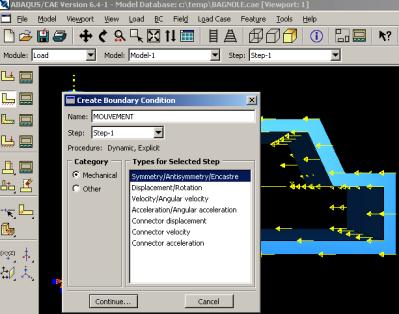
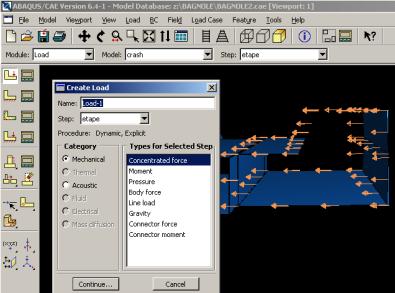
L’utilisateur définit le système à partir de ‘Create Boundary Condition’ et de ‘Create Load’ :
La partie ‘BC’ regroupe tous les mouvements possibles que l’on rencontre, le nombre de degrés de liberté pour chaque pièce.
La partie ‘Load’ regroupe l’ensemble des forces auxquelles le système est soumis.
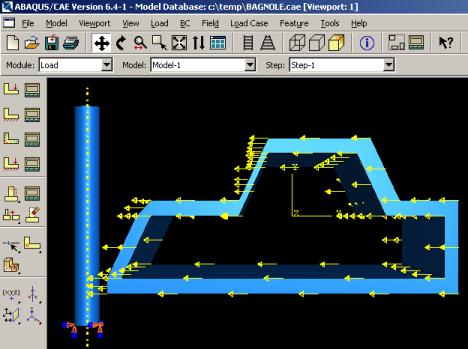
A la page suivante, nous voyons les deux fenêtres en question :
Création du mouvement et définition des encastrements :
Création des forces :
Septième module : Mesh
Voici les pièces telles qu’elles se présentent dans le menu maillage
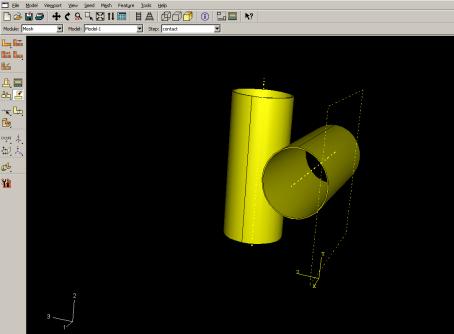
Afin qu’ABAQUS maille correctement, il faut remplir des conditions satisfaisantes et facilitant le calcul numérique, dans le module ‘Mesh’. En effet, l’art du maillage repose essentiellement sur deux critères : Les éléments de maillage (par exemple, hexaédriques, cubiques, tétraédrique dans « Mesh Control ») et la complexité topologique de chaque pièce. Plus la difficulté est accrue, plus la couleur se rapproche du rouge, et inversement, plus le maillage sera aisé, plus la pièce se verra colorée en vert. Ainsi, elles doivent être nécessairement partitionnées, dans l’optique d’optimiser le temps de calcul ou CPU, via l’outil « create partition ».
La partition est intiment liée à trois grands types : ’Edge’, ‘Face’ et ‘Cell’.
Plusieurs méthodes s’offrent aux utilisateurs. La coupe d’une face ou d’une arête. Puis, il faut choisir avec quelle géométrie on va partitionner la pièce (un plan, une courbe …).
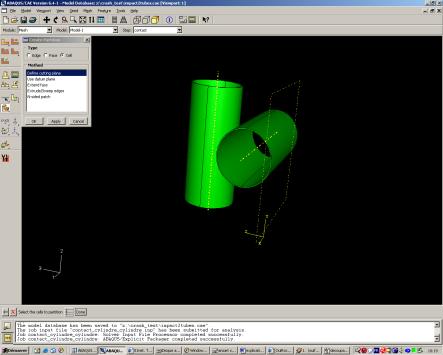
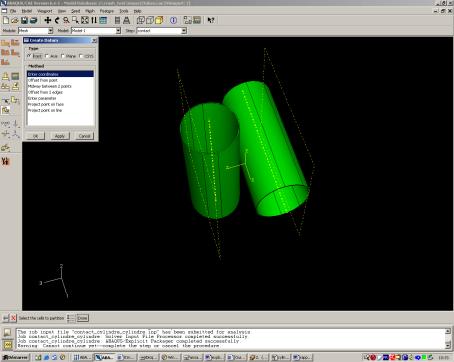
Dans l’exemple traité, il faut initialement créer un plan de coupe, avec « create datum », puis choisir sa méthode de création, en positionnant le plan de coupe via trois points.
Finalement, le cylindre (pièce sélectionnée) est découpé par « define cutting plane ».
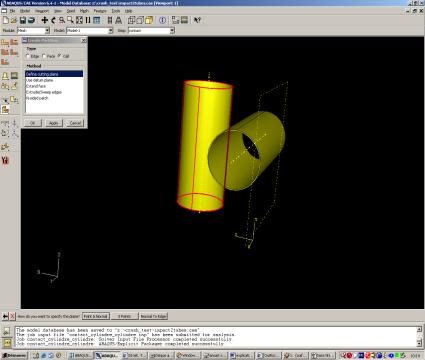
Cette partition est réalisée, pour les cylindres, dans le
sens de la longueur :
Elle est aussi utile pour redéfinir des zones plus importantes, c’est à dire, de pouvoir mailler différemment une même pièce pour mettre en exergue les surfaces de déformation aux endroits « désirés ».Il n’est pas forcément important de mailler trop finement l’ensemble.
Le menu « Mesh Control » :
est l’outil rassemblant l’ensemble des éléments utilisables par Abaqus.
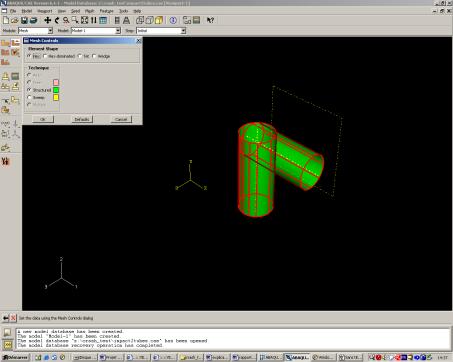
La fonction « hexa-dominated » est une des plus intéressantes puisqu’elle combine deux systèmes de maillage, deux éléments différents: l’hexaèdre et le tétraèdre). Le maillage se construit prioritairement avec des hexaèdres; si le logiciel rencontre une difficulté, lié à l’hétérogénéité des structures, ce dernier utilisera, par défaut, le type tétraédrique.
L’utilisateur définit la taille des éléments grâce à l’outil ‘Instance’, dans le menu ‘Seed’.
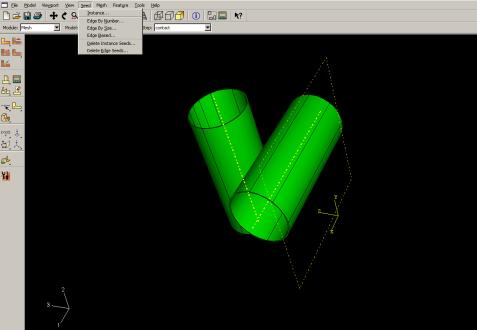
Ainsi, il est possible de resserrer le maillage aux endroits les plus significatifs pour notre étude ou l’élargir aux endroits où une précision importante n’est pas nécessaire.
Il faut impérativement choisir les arêtes dans lesquelles la taille des éléments varie, « edge biased » dans le menu « seed », et lui affecter un coefficient, qui indique le nombre d’éléments voulus sur ces arrêtes :
Nous obtenons la répartition suivante :




![]()
![]()
![]()
![]()
Avec un coefficient de 4, nous avons des éléments de tailles différentes.
« seed part instance » détermine le nombre d’éléments sur le reste du cylindre. Ici, il détermine tout simplement leur taille.
« mesh instance » ou « mesh region » est l’outil pour visualiser le maillage définie auparavant:
Voici l’aperçu de ce maillage :



Cette partie du cylindre est constitué de trois éléments de tailles différentes, (cf. « edge biased »), plus grands que le reste du maillage du cylindre.
Il n’est pas nécessaire d’avoir des tailles différentes; pour cela, il suffit de mettre le coefficient à 1. D’autres fonctions peuvent entrer en ligne de compte comme « edge by number » ou « edge by size »: choix du nombre ou de la taille des éléments sur la petite zone.
La taille ou le nombre d’éléments déterminés par l’utilisateur ne sont que des indices pour le logiciel; il redéfinit le nombre ou la taille minimal des éléments assurant une bonne continuité du maillage avec le reste du cylindre.
Ainsi, en utilisant la fonction « edge biased » avec un coefficient égal à 1, nous en obtenons 3 :

Finalement, il reste le deuxième cylindre à mailler.
Huitième module : Job
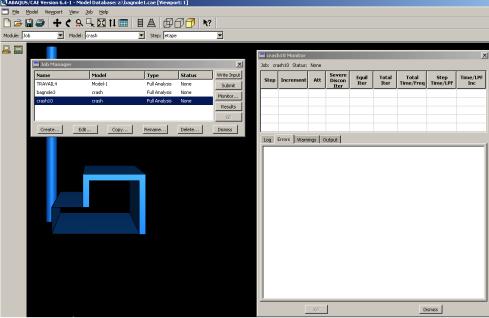
Le module ‘Job’ reprend les caractéristiques de calcul dans le module ‘Step’.
Nous pouvons lancer plusieurs calculs différents.
Neuvième module : Visualisation
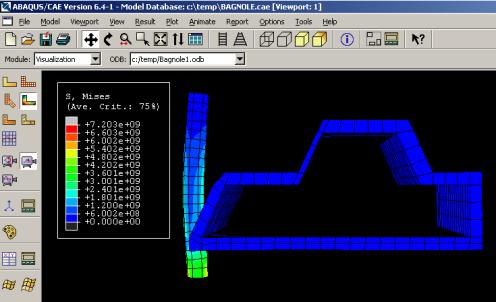
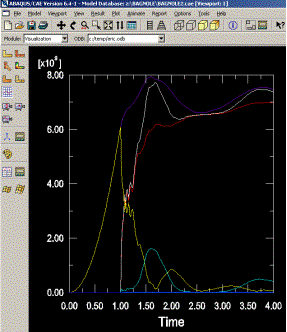
L’utilisateur voit le résultat du calcul numérique dans ‘Result’ : soit par la visualisation des déformations dans ‘Field Output’ : Par Exemple, les déformations, les contraintes, les vitesses ou les forces nodales ; soit par les courbes dans ‘History Output’ : Par exemple, l’énergie cinétique ou l’énergie totale de l’ensemble du modèle, l’énergie de dissipation ou des déformations.
Transfert d’un CAO vers Abaqus :
La plupart des logiciels de CAO sont munis de formats compatibles pour l’import de fichiers vers des logiciels de calcul. Le format d'export IGES est très répandu dans le monde de la CAO. Il peut décrire les données 2D et 3D.
Outre les préliminaires graphiques habituelles telles que la ligne ou le
cercle, ce format permet de décrire des éléments très complexes.
I-Deas Abaqus Solid Works Catia
|
Importation |
|
Qu'est-ce que peut bien signifier «Importer»
un fichier?
|
|
Exportation |
|
L'exportation d'un fichier dans un autre
format est l'inverse de l'importation.
|
|
Pertes à la transmission |
|
L'importation d'un fichier n'est donc rien
d'autre qu'une traduction.
Lors de l'importation de fichiers de dessins, la procédure est similaire. De nombreuses données peuvent être intégralement transmises, avec malgré tout un reste contenant des détails spécifiques au programme. Cette traduction «approximative» entraîne hélas toujours des pertes, comme par exemple les pertes des propriétés d'un objet pendant le transfert.
Les pertes sont encore plus graves quand un élément ne peut pas être converti de façon adéquate. |
De nombreuses données peuvent être intégralement transmises, avec malgré tout un reste contenant des détails spécifiques au programme.
Ce problème nous l’avons rencontré lors d’un transfert de données de CATIA vers ABAQUS. Cependant ce problème n’a pas été rencontré en transférant des données de SOLID WORKS vers ABAQUS.
Remarque : D’autres formats de transferts de données existent, mais notre exemple a été porté sur le format IGES.
V. Apprentissage par exercices
Afin d’appréhender le logiciel, nous avons réalisé plusieurs types d’exercices simples.
Tout d’abord, réaliser la chute d’une bille d’acier sur une plaque en acier représentant le sol, pour ainsi observer les déformations et les rebonds de cette bille.
La bille est lâchée à une hauteur de 20 cm et n’a pour condition initiale que la gravité.
L’épaisseur de la plaque est de 15 mm et celle de la bille est de 1 mm.
Sur cet exercice, nous pouvons voir un résultat qui semble physique, la bille rebondit et perd de la hauteur à chaque rebond. Cela correspond à la perte d’énergie de la bille vers la plaque; de plus, nous constatons que la plaque et la bille encaissent des efforts.

Total des pertes d’énergie dans le temps
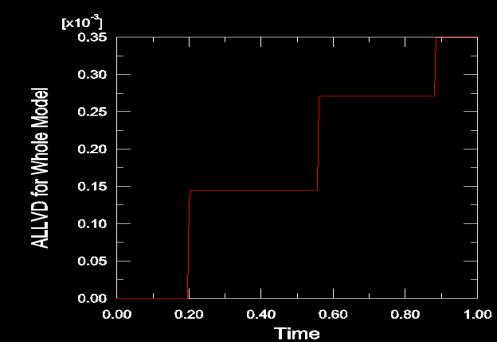
Nous ne constatons cependant aucune déformation, ni de la bille, ni de la plaque (au vu des conditions initiales, cela semble normal que la plaque ne subisse aucune déformation perceptible).
Pour résoudre ce problème, nous avons rajouté le domaine des déformations plastiques et nous avons diminué l’épaisseur de la plaque à 1.5 mm. La plaque est encastrée/libre et la bille est à une hauteur de 10 cm:

Les déformations de la plaque et de la bille sont visibles sur cette vidéo à l’aide de la fonction « scale factor ». Cela nous permet de visualiser les déformations avant le contact.
Nous constatons bien une déformation de la plaque et de la bille, cependant cela nous paraît extrêmement exagéré. En effet l’homogénéité des unités n’a pas été respectée.
En modifiant les unités nous obtenons un résultat tout à fait comparable à celui du livre « FINITE ELEMENT PROCEDURES FOR CONTACT-IMPACT PROBLEMS » de Zhi-hua ZHONG page 227
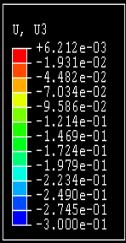 Déplacement
vertical
Déplacement
vertical
![]()
Ensuite, nous avons rajouté la pesanteur sur la plaque (utilisation de Conditions Initiales et Conditions Limites).

La bille rebondit et prend une autre direction suite à l’angle d’attaque avec la plaque, cependant la bille se déforme peu mais, cela ne semble pas faux vu l’épaisseur de la plaque. Le résultat semble correct.
Par la suite nous avons augmenté le diamètre de la bille (4mm):

Ici, la bille étant très lourde par rapport à la plaque, elle va rouler sur celle-ci après l’avoir déformée. Utilisation des lois de déformation plastique.
Le modèle suivant est constitué de deux plaques. Il faut gérer deux contacts différents en même temps (bille/plaque et plaque/plaque), ainsi que le frottement entre les deux plaques.
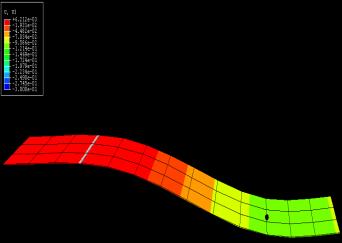
Les déformations observées ressemblent à celles du livre cité précédemment p258. Le modèle semble bon.
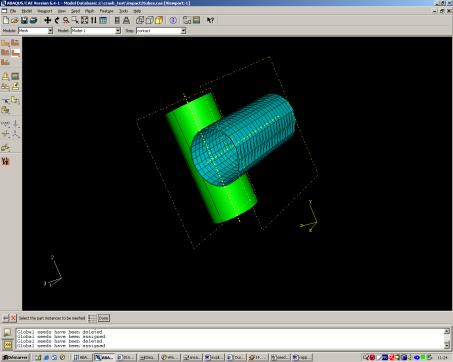
Contact entre deux tubes
Nous avons essayé de réaliser l’impact entre deux tubes. Contact difficile à gérer car il s’effectue sur deux surfaces non planes.
Création de la pièce :
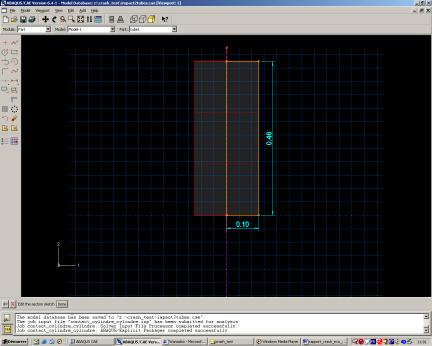
Pour réaliser un tube, nous avons d’abord créé un cylindre plein
que nous avons ensuite percé aux dimensions du modèle, à savoir : 0,46 m
de hauteur, 0,103 m de diamètre extérieure et 0,1 m de diamètre intérieure.
Propriétés du matériau :
-densité de 7840 Kg.m-3
-module d’Young de 2 E+11 Pa
-coefficient de poisson de 0.3
-déformations plastiques :
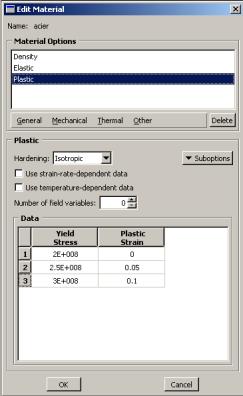
Assemblage :
Création du contact entre ces 2 tubes en dynamique explicite en incluant les déformations non linéaires;
Création de l’interaction entre ces deux tubes :
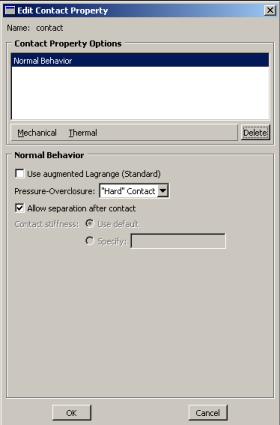
Mais également l’interaction entre chaque tube eux même :
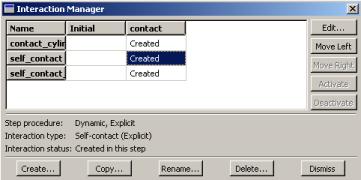
Mise en place des charges :
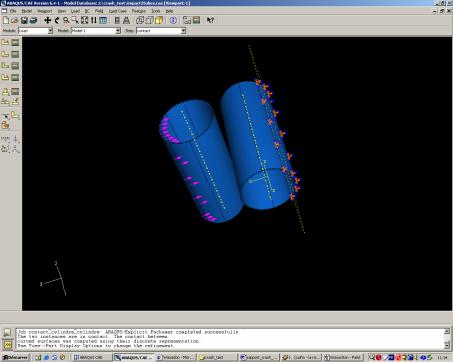
Nous avons donc donné une vitesse à l’un des tubes alors que l’autre est encastré sur une partie.
Si la vitesse est appliquée sur l’ensemble du cylindre, celui-ci ne se déforme qu’en présence de la partie encastrée de la seconde pièce. Afin que les deux pièces se déforment en même temps, la vitesse est appliquée sur une partie du cylindre.
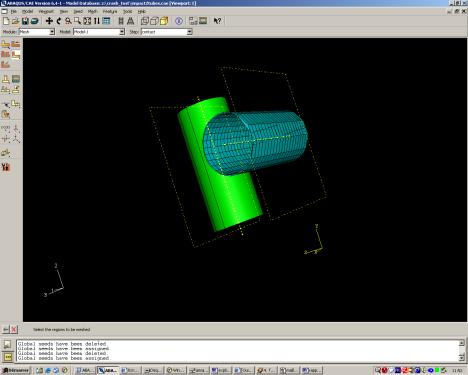
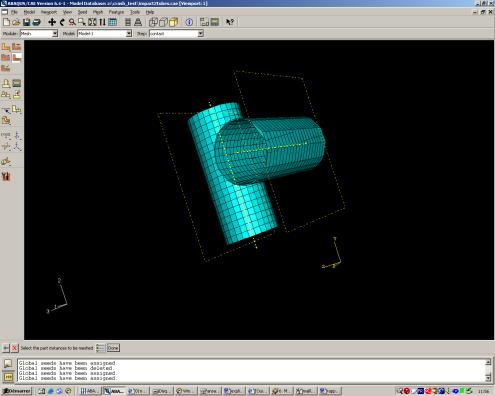
La dernière étape est le maillage de ces deux tubes, pour cela, il a donc fallu couper chaque tube pour qu’ils puissent être maillés correctement :
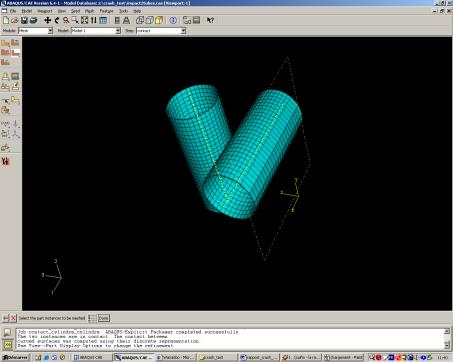
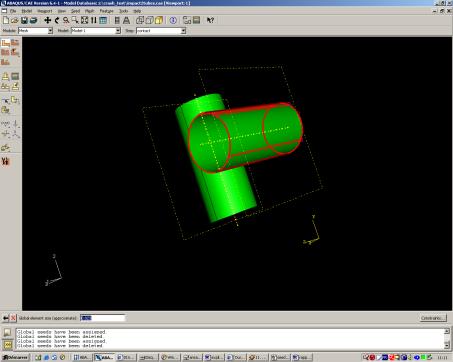
Nous avons raffiné le maillage sur les surfaces en contact pour avoir un résultat assez précis. Sur la partie encastrée, cette partie ne nous intéressant pas du fait qu’elle ne bouge pas, le maillage est plus grossier.
La déformée de ce modèle n’est pas totalement physique étant donné que les C.I. (vitesse) ne sont pas appliquées correctement. Problème dont nous n’avons pas trouvé la solution.
L’ensemble des exercices précédents nous a permit d’apprendre à utiliser correctement la saisie des données nécessaires au problème d’un crash d’une voiture tant pour les données des matériaux, que pour les C.I. et C.L. ainsi que pour les lois de comportement (déformations plastiques…).
Création d’un modèle très simplifié d’une voiture(silhouette de la carrosserie).
Impact d’une voiture sur un mur indéformable à 15 m.s-1.
Définition des matériaux : acier ordinaire.
Utilisation de la loi de déformation plastique et de déformation non linéaires .
Interactions tangentielles et normales.
![]()
Le modèle de la voiture étant trop simplifié, les déformations correspondent à celui ci mais ne sont pas réaliste vis à vis d’un véhicule existant. L’application des C.I. et C.L. semble bonne.
Impact frontal entre deux voitures ; l’une est fixe et l’autre a une vitesse de 20m.s-1.
Définition des matériaux : acier ordinaire.
Utilisation de la loi de déformation plastique et de déformation non linéaires .
Interactions tangentielles et normales.

Ce modèle nous permet de visualiser le transfert d’énergie entre les deux véhicules au moment de l’impact.
L’utilisation conjointe de deux hypothèses, dont l’une porte sur la nature du matériau, résultant directement par l’introduction de déformation plastique dans le module ‘property’ appelée ‘Crushable Foam’ en option ‘Crushable Foam Hardening’, et l’autre sur l’habitacle, plus précisément, sur la rigidité de cette dernière nous permet d’approcher plus près de la réalité.

Ne disposant pas de modèle numérique de voiture, nous nous sommes arrêtés à ce stade.
Ce projet confié au début de l’année nous a permit de découvrir la mécanique non linéaire à travers le crash test et le logiciel Abaqus.
Etant parti de rien, et personne sur le campus ne connaissant le fonctionnement d’Abaqus, nous avons dû apprendre par nous même avec l’aide de cours trouvés sur Internet et d’exercices.
Ce fût une expérience très enrichissante d’un point de vu technique et humain. En effet chaque participant du groupe travaillant sur des points différents du projet faisait par de son expérience acquise au fur et à mesure.
Finite Element Procedures for
CONTACT-IMPACT PROBLEMS
Oxford Science publications ZHI-HUA ZHONG