Jeux Mathématiques et Logiques

service maintenu par Gilles HAINRY, agrégé de mathématiques,
Université du Maine
I.U.T. Techniques de Commercialisation
53000 LAVAL
(France)

email : gilles.hainry_at_univ-lemans.fr

Formats de papier et racines

© Gilles HAINRY, Université du Maine

Cloche, Couronne, Ecu, Cavalier, Raisin, Jésus, Colombier, Univers...

Quel est donc le rapport entre ces mots ?

La réponse est simple et tous les cyberlecteurs - en particulier ceux qui lisent aussi livres et cahiers - sont concernés puisqu 'il s'agit de formats de papier ; des formats associés aux dimensions d'une feuille de papier : ainsi le format "cloche" correspond à une largeur de 30 cm et une longueur de 40 cm; le "raisin" à 50 cm x 65 cm. le "jésus" à 56 cm x 76 cm; l'"univers" à 100 cm x 130 cm ...
Une feuille de papier est généralement destinée à être pliée (voire coupée) en deux, quatre, huit, seize pour donner les pages d'un même livre ou journal. Ainsi, un in-quarto -ce qui veut dire "en quatre"- est une feuille qui a subi deux plis pour donner 4 feuillets (2x2), soit 8 pages. Les pages d'un in-quarto jésus mesurent 28 cm x 38 cm : celles d'un in-seize jésus 14 cm x 19 cm (elles ont été pliées 4 fois, ce qui donne 16 feuillets -2x2x2x2-, donc 32 pages)...

Les formats cités plus haut, pour la plupart très anciens, ont deux inconvénients majeurs :
- La surface d'une feuille de papier est un nombre compliqué ;
- Les proportions de la feuille (rapport longueur / largeur) ne sont pas conservées lorsque celle-ci est pliée ou coupée en deux (deux parties égales).

Afin de remédier à ces inconvénients, on a cherché - et trouvé - un format tel que la surface d'une feuille soit 1 mètre carré et que ses proportions soient conservées lors d'un pliage le long de la plus petite de ses médianes.

Reprenons les hypothèses :

la feuille a une longueur L (en mètres)
et une largeur w (en mètres)
telles que L . w = 1 (surface en mètres carrés)

la demi-feuille a pour longueur w
et pour largeur L / 2
bien sûr sa surface est 1 /2 mètre carré.
surtout, on veut L / w = w / (L / 2)
On en tire, en posant L / w = x, l'équation x = 2/x,
soit x ^ 2 = 2.;

Le nombre x = L / w est l'unique nombre positif dont le carré vaut 2 ; on l'appelle la racine carrée de 2.
On écrit L / w = 2 ^ (1/2).
Une calculatrice montre que 2 ^ (1/2) = 1,414...

Il vient x = 2 ^ (1/2), soit L = w . 2 ^ (1/2).
En remplaçant w par 1/L, on trouve que
L ^ 2 = 2 ^ (1/2) c'est à dire L ^ 4 = 2.

Le nombre positif qui vérifie cette équation est unique et s'appelle la racine quatrième de 2.
On écrit L = 2 ^ (1/4) ou encore L = (2 ^ (1/2)) ^ (1/2)
Une calculatrice en donne la valeur approchée L = 1,189... et pour son inverse w = 0,841...

LA SERIE NORMALISEE

La feuille de 1 mètre carré de format normalisé international (dont on vient de calculer les longueur et largeur) est représentée par le symbole A0, la demi-feuille par A1, le quart de feuille par A2 dans le tableau ci-dessous (valeurs approchées)

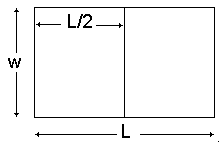
Format	Longueur	Largeur	Surface	L/w
	(en mm)		(en mm²)
A0	1189	841	1000000	1,414
A1	841	595	500000	1,414
A2	595	420	250000	1,414
A3	420	297	12500	1,414
A4	297	210	62500	1,414
A5	210	148	31250	1,414

On retrouve bien sûr le très fameux format A4 (21 cm x 29,7 cm) et on vérifie que L/w ne change pas : c'est un invariant de la série normalisée. Nous avons vu plus haut que L/w = 2 ^ (1/2).

Exercices

1) Une feuille de 1 mètre carré pèse 80 g. Une enveloppe et son timbre pèsent 3g . Combien de feuilles de format A4 peut-on mettre dans l'enveloppe
a) si celle-ci est timbrée à 3,00F ? (maximum 20g)
b) si elle est timbrée à 4,50F ? (maximum 50g)

2) Combien faut-il de feuilles de format Ao pour réaliser un livre de 192 pages de format A5 ?

3) Déterminer la longueur et la largeur d'une feuille de format A10.

Réponses

1) On montre d'abord qu'une feuille de format A4 pèse 5 g ;
alors, on trouve :
pour a) 3 feuilles
pour b) 9 feuilles.

2) Il y a 2 ^ 5 = 32 feuilles A5, soit 64 pages dans une feuille A0 ;
il en faut donc 3.

3) Le lecteur trouvera tout seul ; s'il réussit, ce dont nous ne doutons pas, il pourra vérifier que longueur + largeur = 63 mm.

Accueil	Articles	Problèmes
Q.I.	Calendriers	Révolution

4 février 1999