Jeux Mathématiques et Logiques
service maintenu par
Gilles HAINRY, agrégé de mathématiques,email : gilles.hainry_at_univ-lemans.fr
Solutions des
Problèmes (Troisième série)
©
Gilles HAINRY
1. PUCES PARTIE.
Mon chien a trois fois plus de puces qu'il n'a d'oreilles. Chacune des puces a invité trois autres puces pour une surprise partie.
Combien y a-t-il de puces sur le dos de mon chien, sachant qu'il entend très bien leur musique de ses deux oreilles ?
Kzav, mon chien, a deux oreilles, et donc six puces "à lui" ;
chacune ayant invité trois amies, il y a dix-huit puces invitées.
D'où un total de vingt-quatre puces sur le dos de Kzav.
Bonne réponse de :
Ecole Alain, de Laval (Mayenne, France)
entre autres
Voulez vous
revenir au menu ?
2. UNE FAIM D'OGRE.
Un ogre a un très gros appétit. Pour se rassasier après un long voyage, il mange sans s'arrêter pendant deux heures, sept minutes et douze secondes, un poulet ou un canard par seconde.
Combien lui faudra-t-il de volailles pour assouvir sa faim ?
2 heures font 7200 secondes ;
7 minutes font 420 secondes ;
7200 + 420 + 12 = 7632.
Il lui faudra 7632 secondes pour se rassasier.
Bonne réponse de :
Olivier Santin, de Copenhague (Danemark)
entre autres
Voulez vous
revenir au menu ?
3. UNE SOIF D'OGRE.
Un ogre pèse 1998 kg . Lorsqu'il a soif, il peut boire le tiers de son poids en eau.
Combien de litres peut-il boire sachant que un litre d'eau pèse un kg ?
1998 / 3 = 666.
il peut boire 666 litres d'eau.
Bonnes réponses de :
Larry Boccara et Léo Maksud, de Laval (Mayenne, France)
entre autres
Voulez vous
revenir au menu ?
4. FEUILLES MULTICOLORES !
100 enfants sont assis à des places numérotées de 1 à 100.
On donne une feuille rose au n°1, une blanche au n°2, une bleue au n°3, une rose au n°4, un blanche au n°5, une bleue au n°6... et ainsi de suite.
Une feuille sur quatre, en commençant par la quatrième est décorée d'une frise.
Quel est le numéro de la place du premier enfant ayant une feuille
bleue décorée ?
De quelle couleur sera la feuille de l'enfant assis à la soixante-quatorzième place ?
Sera-t-elle décorée ?
Numéros associés aux feuilles bleues :
3 ; 6 ; 9 ; 12 ; 15 ; 18 ; 21 ; 24 ; 27 ; 30 ...
(ce sont les multiples de 3)
Numéros associés aux feuilles décorées :
4 ; 8 ; 12 ; 16 ; 20 ; 24 ; 28 ...
(ce sont les multiples de 4)
La place du premier enfant ayant une feuille bleue décorée a donc le numéro 12.
(c'est le plus petit multiple commun (ppmc) de 3 et de 4.)
72 est un multiple de 3 : feuille bleue ;
ainsi, 73 correspond à rose et 74 à blanche (comme 2, qui est le reste de la division de 74 par 3).
L'enfant assis à la soixante-quatorzième place a donc une feuille blanche ; elle n'est pas décorée, parce que 74 n'est pas un multiple de 4.
Bonnes réponses de :
Quentin Woitiez, de Laval (Mayenne, France) et de Philippe Roulin de Suisse
entre autres
Voulez vous
revenir au menu ?
5. ET MOIS, ET MOIS ET MOIS.
Dans la cour du centre universitaire de Laval,
Antoine et Coralie se posent des devinettes.
Antoine : Quel est le mois le plus court ?
Coralie : Février bien sûr !
Antoine : Perdu ! C'est mai qui s'écrit seulement avec trois lettres..
.
Laissez Coralie et Antoine discuter et répondez aux
deux questions suivantes:
1) Parmi les douze mois de l'année, certains s'écrivent avec des lettres
toutes differentes; lequel d'entre ceux-ci utilise le plus de lettres ?
2) Combien de lettres de l'alphabet ne sont pas utilisées dans l'écriture des noms des
douze mois ?
1. janvier : 7 lettres ; février : 7 lettres ;
mars : 4 lettres ; avril : 5 lettres ; mai : 3 lettres ;
juin : 4 lettres ; juillet : 7 lettres ; août : 4 lettres ;
septembre : 9 lettres ; octobre : 7 lettres ; novembre : 8 lettres ;
décembre : 8 lettres.
le mois le plus long est septembre, mais, les seuls mois s'écrivant avec des lettres toutes différentes sont :
janvier (7 lettres) ; mars (4 lettres) ; avril (5 lettres) ; mai (3 lettres) ; juin (4 lettres) ; août (4 lettres).
la réponse est donc janvier.
2. notons les lettres utilisées : a, b, c, d, e, f, i, j, l, m, n, o, p, r, s, t, u, v.
Il reste g, h, k, q, w, x, y, z soit 8 lettres non utilisées.
Bonnes réponses de :
Léo Maksud et Quentin Woitiez, de Laval (Mayenne, France)
entre autres
Voulez vous
revenir au menu ?
6. LA TACHE.
Dans l'opération ci-dessous, une tâche a malheureusement
effacé un chiffre :
19#1 x 1992 = 3 946 152
.
Quel est le chiffre caché par la tâche ?
Avec une calculette, ou à la main, on voit que
3 946 152 / 1992 = 1981.
Le chiffre caché est donc un 8.
Beaucoup plus élégant est sans doute le recours à la preuve par 9.
Bonnes réponses de :
Olivier Santin, de Copenhague (Danemark) et Philippe Roulin de Suisse
entre autres
Voulez vous
revenir au menu ?
7. A CHACUN SA VOITURE.
Neuf enfants veulent chacun une petite voiture .
Il y a 3 modèles différents : une mini, une 2CV, une coccinelle.
Il y a 4 couleurs différentes disponibles : rouge, vert, jaune, bleu.
Chaque enfant pourra-t-il avoir une voiture différente
(modèle ou couleur) ?
Combien de voitures différentes peut-on avoir ?
Il existe 4 x 3 = 12 voitures
différentes et la réponse à la première question est donc Oui.
Bonnes réponses de :
Larry Boccara, Quentin Woitiez, Léo Maksud, de Laval (Mayenne, France)
entre autres
Voulez vous
revenir au menu ?
8. L'ECOLE DE TROUPERDU.
Dans l'unique classe de Trouperdu, petit village
de campagne, il n'y a que neuf élèves :
-Les trois enfants du boulanger : Isabelle, Ursule et Tony CALEPIN.
-Les trois enfants du boucher : Isabelle, Ursule et Tony BOEUFMODE.
-Les trois enfants de l'instituteur : Isabelle, Ursule et Tony ANALYSE.
Monsieur Analyse, le maître d'école, d'abord surpris que les enfants Boeufmode
et les petits Calepin portent les mêmes prénoms que ses propres enfants, décide,
pour éviter toutes confusions, de répartir ses 9 élèves de façon à ce qu'aucune
des 3 lignes (horizontales) ni aucune des 3 colonnes (verticales) de bureaux ne
contienne deux enfants de la même famille ou ayant le même prénom.
Compléter le plan de la classe.
Isabelle ANALYSE Ursule BOEUFMODE **************** Tony BOEUFMODE **************** **************** **************** **************** ****************
Isabelle ANALYSE Ursule BOEUFMODE Tony CALEPIN Tony BOEUFMODE Isabelle CALEPIN Ursule ANALYSE Ursule CALEPIN Tony ANALYSE Isabelle BOEUFMODE
Bonne réponse de :
Caroline Merchez de Sceaux (France)
entre autres
Voulez vous
revenir au menu ?
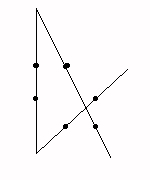
9. LE TRACE
Tracer une ligne brisée formée de trois segments de droites et qui passe par les 6 points de la figure ci-dessous.
* *
* *
* *
Une solution :

Bonne réponse de :
Philippe Roulin, de Suisse
entre autres
Voulez vous
revenir au menu ?
octobre 1999
(m à j fév 2000)