
Animations
 |
Animations |
 |
|
La solution de
l'équation des ondes écrite en
coordonnées sphériques (r,
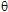 , ,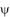 ) ) 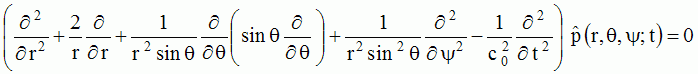 , ,s'écrit,
pour les solutions à variables
séparées cherchées sous la forme
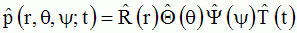 , ,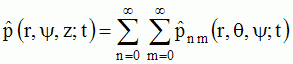 avec avec
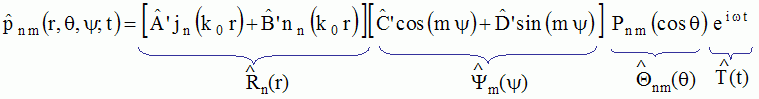 où les
fonctions jn et nn
sont respectivement les fonctions de Bessel sphériques de
première espèce et les fonctions de Neumann
sphériques, d'ordre n, et où les fonctions Pnm(cos
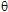 ) sont les
fonctions de Legendre, qui peuvent être
exprimées en fonction des polynômes
de Legendre de degré n, notés Pn,
de la manière suivante (ne pas confondre les fonctions Pnm
et les polynômes Pn) : ) sont les
fonctions de Legendre, qui peuvent être
exprimées en fonction des polynômes
de Legendre de degré n, notés Pn,
de la manière suivante (ne pas confondre les fonctions Pnm
et les polynômes Pn) :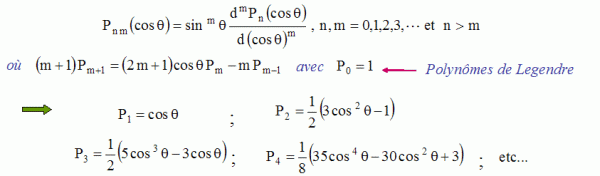 Les fonctions
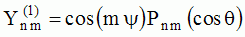 et et 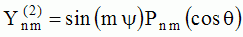 sont
appelées "harmoniques sphériques". sont
appelées "harmoniques sphériques".Par suite, toute solution à variable séparée a, pour n et m donnés, une structure bien déterminée sur la sphère unité (paramètres 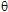 et et 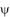 ).
Cette structure est donnée par les harmoniques
sphériques, fonctions orthogonales qui forment une base de
l'espace ( ).
Cette structure est donnée par les harmoniques
sphériques, fonctions orthogonales qui forment une base de
l'espace (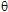 , ,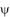 )
considéré. )
considéré.Ces formes de solutions traduisent une directivité complexe des champs émis, dans l'espace infini, par un ensemble de sources "localisées" aux propriétés complexes. |
|
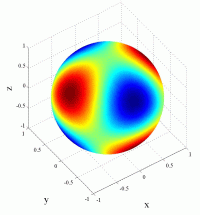
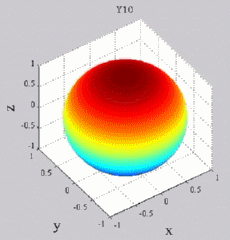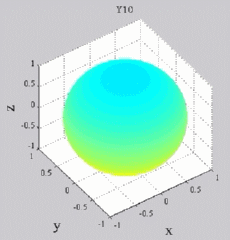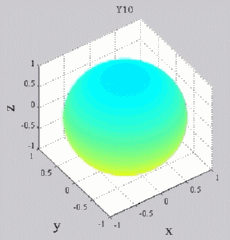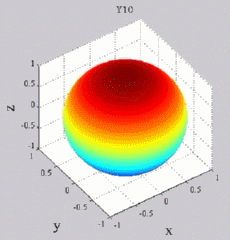
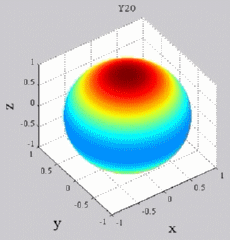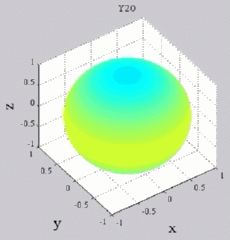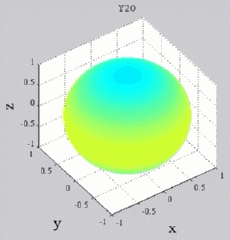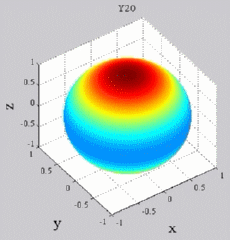
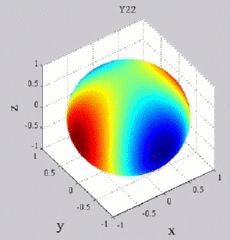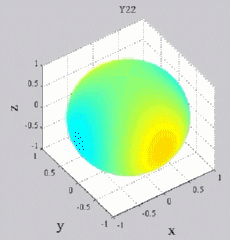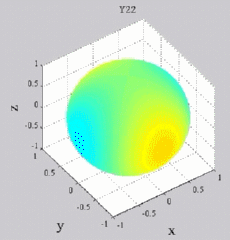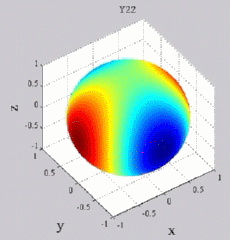
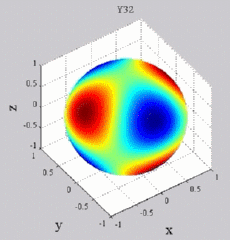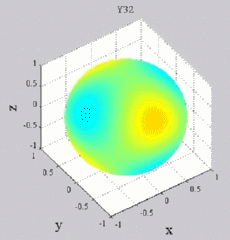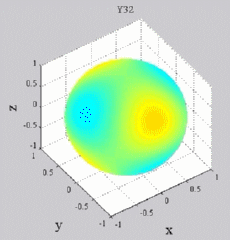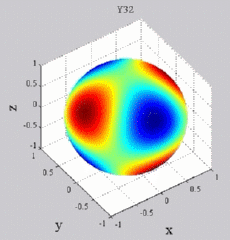
Les
animations ci-dessous présentent les variations en fonction
du temps des premiers harmoniques sphériques 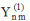 multipliés par la fonction cos(
multipliés par la fonction cos(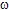 t),
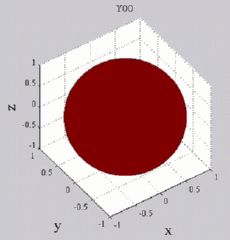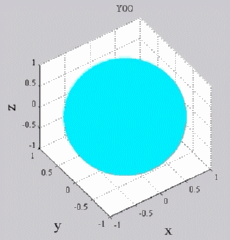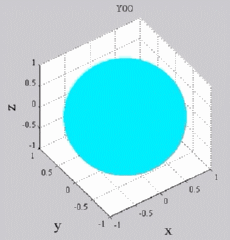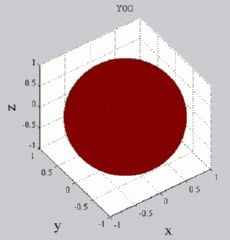
visualisées sur la sphère unité, en
niveaux de couleurs (rouge =
maximum, bleu = minimum). t),
visualisées sur la sphère unité, en
niveaux de couleurs (rouge =
maximum, bleu = minimum). |
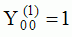  |
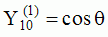  |
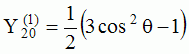  |
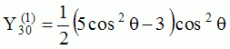  |
| Harmoniques
"zonaux" : m=0 Harmoniques "sectoraux" : n=m |
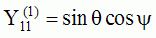  |
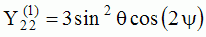  |
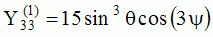 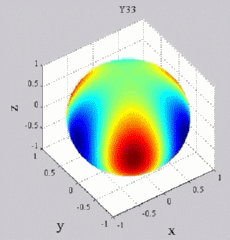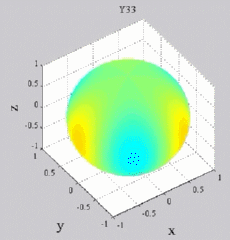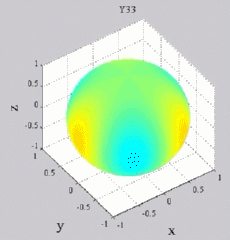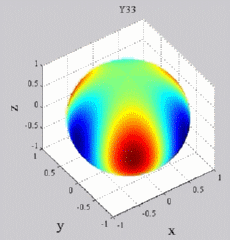 |
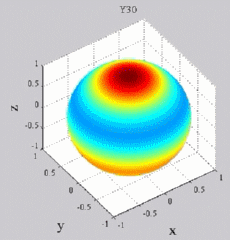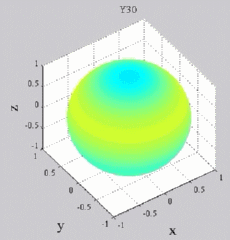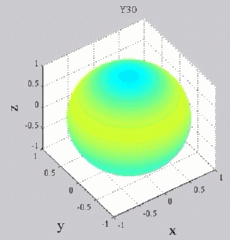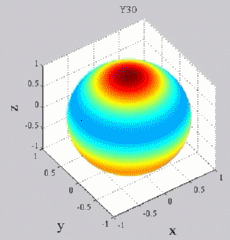
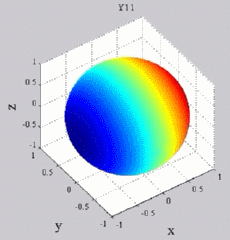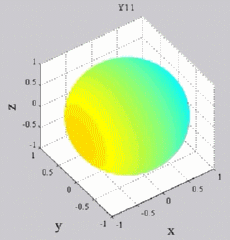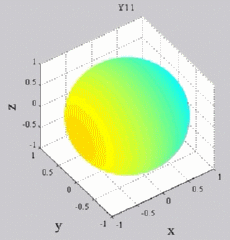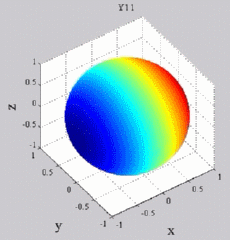
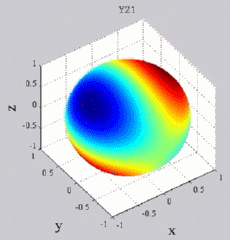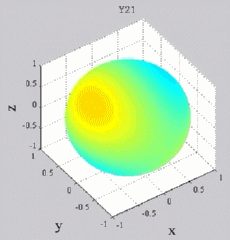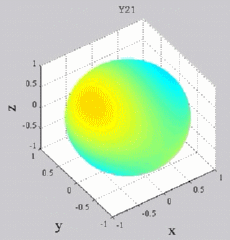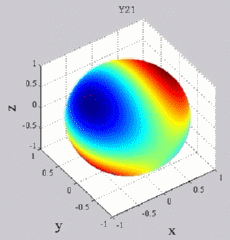
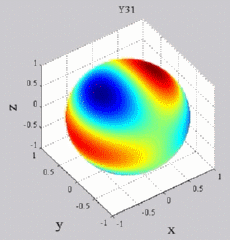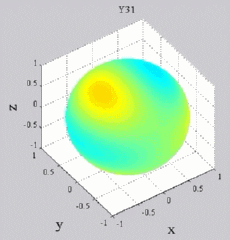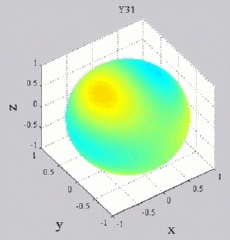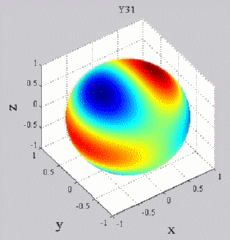
| Harmoniques
"tesséraux" : 0<m<n |
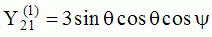  |
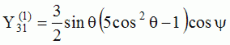  |
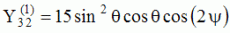  |