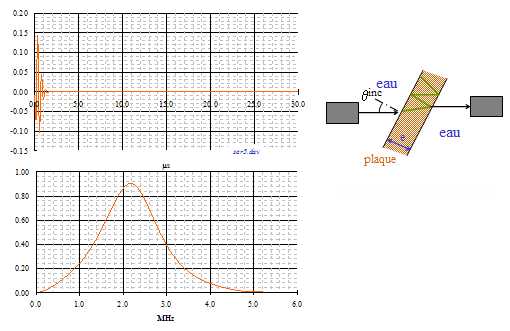
Fig. 1 |
Dans le
domaine de l'Evaluation et du Contrôle Non Destructifs par
ultrasons, le signal
d'entrée prend le plus souvent la forme d'une
impulsion ou d'un train d'onde.
La figure 1 présente un exemple de signal
impulsionnel, la fréquence centrale du
transducteur étant égale à 2.2 MHz
(voir le module de la transformée de Fourier du signal
temporel, bas de la figure 1).
Les traitements de base portent d'une part sur la mesure des
temps de
vol entre les différents échos
contenus dans les signaux réfléchis ou
transmis par le matériau étudié
(mesure directe, transformée de
Hilbert, utilisation d'ondes guidées, …), et
d'autre part, sur
l'analyse des variations d'amplitudes associées (plus
généralement, sur
l'analyse de toute propriété porteuse
d'information). Les informations
contenues dans ces signaux ne sont cependant accessibles que dans la
mesure où les multiples
échos sont séparables. |
Fig. 2
cliquez
sur l'image pour avoir une meilleure définition
|
La figure 2 montre
les signaux réfléchis et transmis (simulation)
par une plaque d'aluminium d'épaisseur h plongée
dans l'eau, lorsque l'axe du transducteur incident fait un angle 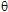 inc avec la normale
à la plaque (signal incident de la figure 1). inc avec la normale
à la plaque (signal incident de la figure 1).
En incidence normale ( inc=0°),
la longueur d'onde inc=0°),
la longueur d'onde  L
est suffisamment petite par rapport à l'épaisseur
h pour que les différents échos soient bien
séparés. Une simple mesure du temps L
est suffisamment petite par rapport à l'épaisseur
h pour que les différents échos soient bien
séparés. Une simple mesure du temps  d'aller-retour des ondes longitudinales
entre les deux interfaces de la plaque permet, par une formule simple,
d'en déduire la vitesse de propagation VL
des ondes longitudinales. d'aller-retour des ondes longitudinales
entre les deux interfaces de la plaque permet, par une formule simple,
d'en déduire la vitesse de propagation VL
des ondes longitudinales.
Lorsque l'incidence augmente, les échos correspondant aux
ondes transversales apparaissent, et, bien que là encore il
soit possible de mesurer des temps de vol, les échos
commencent à se mélanger. |
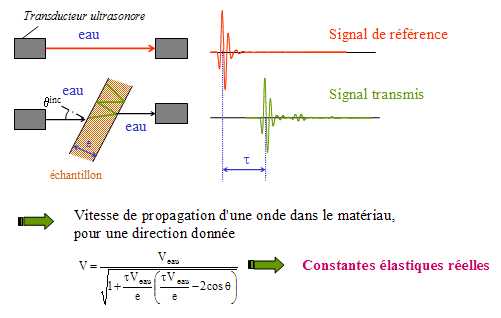
Fig. 3 |
La méthode
de base classique en ultrasons pour
déterminer les constantes élastiques du
matériau constituant un échantillon (plaque dans
le cas de la figure 3) consiste à mesurer les vitesses de
propagation des ondes se propageant dans le matériau.
Un premier signal (signal de
référence) est mesuré dans l'eau, sans
échantillon. La même expérience est
ensuite répétée en présence
de l'échantillon, ce qui permet d'obtenir le signal transmis par la plaque.
Les deux signaux n'arrivant pas au
même moment, il y a un décalage temporel 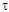 ,
qui permet, connaissant l'angle d'incidence ,
qui permet, connaissant l'angle d'incidence 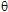 inc, l'épaisseur de la plaque e, et la vitesse de
propagation des ondes dans l'eau Veau, de
déterminer la vitesse V de l'onde se propageant dans
l'échantillon (voir figure 4 pour la
démonstration de la formule). inc, l'épaisseur de la plaque e, et la vitesse de
propagation des ondes dans l'eau Veau, de
déterminer la vitesse V de l'onde se propageant dans
l'échantillon (voir figure 4 pour la
démonstration de la formule).
En procèdant de la
même façon pour différents angles
d'incidence, il est ensuite possible, par un algorithme d'inversion,
d'obtenir les constantes élastiques (Fig. 5).
|
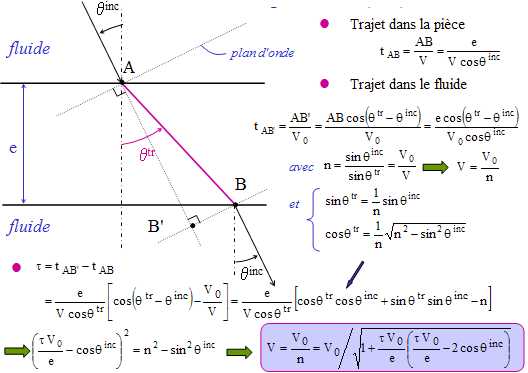 Fig. 4 Fig. 4 |
 Fig. 5 Fig. 5 |
MAIS...
cette
méthode a cependant ses limites : il faut en
effet que l'échantillon soit considéré
comme semi-infini et homogène. Si l'épaisseur de
la plaque est trop petite devant
la longueur d'onde, il sera très difficile de
séparer les échos temporels et donc de mesurer
des temps.
De
plus, au fur et à mesure que l'angle d'incidence augmente,
les échos se déforment, et il
est également difficile d'évaluer les temps
(Fig. 6).
|
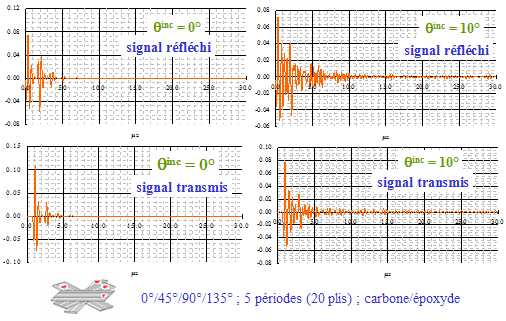
Fig. 6
cliquez
sur l'image pour avoir une meilleure définition
|
La figure 6
illustre ces propos en montrant les signaux
réfléchis et transmis (simulation) par
une plaque composite en carbone/époxyde
d'empilement 0°/45/90°/135° comportant
20 plis (épaisseur 2.6 mm) dans l'eau, lorsque l'axe
du transducteur incident fait un angle 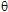 inc inc avec la normale
à la plaque (signal incident de la figure 1).
En incidence
normale ( 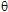 inc inc=0°), il
est encore possible de séparer les échos, mais,
lorsque
l'incidence augmente, les échos correspondant aux ondes
quasi-transversales
apparaissent, et tous les échos sont
mélangés. |




 En
construction...
En
construction...