identification of echoes

Context. Ultrasonic Non Destructive Evaluation and Testing are often based on the estimate of a time-of-flight of the acoustic waves through materials or structures. As the involved sizes can be small compared to the wavelengths of the acoustic signals, it happens that the echoes generated by the various ruptures of impedance (interfaces, defects, inclusions,…) overlap both in time and frequency, whereas it is necessary to suitably separate them in order to be able to determine the properties (in particular viscoelastic) of materials.

Classical method for measuring propagation velocities from a time-of-flight.

Fig. 1	In the field of ultrasonic Non Destructive Evaluation and Testing, the input signal is usually an impulse or a wave train. Figure 1 presents an example of an impulse signal, the central frequency of the transducer being equal to 2.2 MHz (see the modulus of the Fourier transform the time signal, Fig. 1). The basic processes rely, on one hand, on the measurement of times of flight between the various echoes contained in the signals which are reflected or transmitted by the considered material (direct measurement, Hilbert transform, use of guided waves,…), and in addition, on the analysis of the variations of associated amplitudes (more generally, on the analysis of any property carrying information). The information included in these signals is however accessible only insofar as the multiple echoes are separable.
Fig. 2 click on the image for a zoom	Figure 2 shows the (simulated) signals which are reflected and transmitted by an aluminium plate immersed in water (thickness h), when the acoustic axis of the emitter makes an angle ^inc with the normal to the plate (incident signal of Fig. 1). In normal incidence (^inc=0°), the wavelength _L is small enough compared to the thickness h so that the various echoes are quite separated. A simple measurement of go an return time of the longitudinal waves between the two interfaces of the plate allows, by a simple formula, to deduce from it the propagation velocity V_L of the longitudinal waves. When the incidence increases, the echoes corresponding to the shear waves appear, and, although it is still possible to measure times of flight, the echoes start to mix.
Fig. 3	The traditional basic method in ultrasounds used to determine the elastic constants of the material constituting a sample (plate in the case of Fig. 3) consists in measuring propagation velocities of the waves being propagated in material. A first signal (reference signal) is measured in water, without any sample. The same experiment is then repeated in the presence of the sample, which makes it possible to obtain the signal transmitted by the plate. 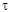As the two signals do not arrive at the same time, there is a temporal shift , which allows, knowing the incident angle ^inc, the thickness of the plate e, and the propagation velocity of the waves in water V_eau, to determine the velocity V of the wave being propagated in the sample (see Fig. 4 for the demonstration of the formula). When doing the same for various incident angles, it is then possible, by an inversion algorithm, to obtain the elastic constants (Fig.5).
Fig. 4
Fig. 5	BUT… however, this method is limited: indeed it is necessary that the sample is considered as a semi-infinite and homogeneous one. If the thickness of the plate is too small compared to the wavelength, it will be very difficult to separate the time echoes and thus to measure times. Moreover, as the incident angle increases, the echoes become deformed, and it is also difficult to evaluate times (figure 6).
Fig. 6 click on the image for a zoom	Fig. 6 illustrates these remarks by showing the signals which are reflected and transmitted in water (simulation) by a carbon/epoxy plate, made up of the stacking 0°/45/90°/135° (20 layers, total thickness equal to 2.6 mm), when the axis of the emitter forms an angle ^inc with the normal to the plate (incident signal of Fig. 1). In normal incidence (^inc=0°), it is still possible to separate the echoes, but, when the incidence increases, the echoes corresponding to the quasi-shear waves appear, and all the echoes are mixed.

Sparse deconvolution method for wave separation ; parametric method. The interferometry methods such as correlation which are generally used to carry out the wave separation, are non-parametric methods (in the sense that no physical a priori is introduced) and can be insufficient in terms of capacity of separation). Consequently, the use of a parametric method (thus based on a descriptive model of the problem) for separation of the waves is proposed, within the framework of the thesis of Aurélien Roux, in joint supervision with Laurent Simon (Pr.). [B17, C13]

Collaboration with Jérôme Idier of the Institute of Research in Communications and Cybernetics of Nantes (IRCCyN).

Under construction. Sorry...

Home page