Microscopy : Fundamentals

Diffraction imposes a resolution limit on the order of the wavelength, when observing objects with an optical system such as a microscope. To quantitatively determine how an image deteriorates due to diffraction, it is interesting to use the object spatial frequency space and to consider the system modulation transfer function (MTF). (See the course on Image Formation in the module Fourier Optics, or the references [ ^[1]], [ ^[2]] .) The theory shows that image degradation does not only depend on the objective properties (numerical aperture, aberrations) but also on the illumination spatial coherence, a property directly related to its numerical aperture.

When the aperture diaphragm is almost closed (point-like source), the object is illuminated with a quasi planar wave, and the illumination is said to be spatially coherent. Fourier formalism can then be applied to the complex amplitudes of waves. In that case, an optical system with no aberration (diffraction-limited) is a low-pass filter for the spatial frequencies: it leaves unaltered all frequencies smaller than \(NA_{obj}/ \lambda\) where \(NA_{obj}\) represents the object-side numerical aperture of the objective and perfectly cuts all larger frequencies (see. Fig. 10, trace 1). In those conditions, images are well contrasted but image elements are circled with fringes related to the Gibbs phenomenon.

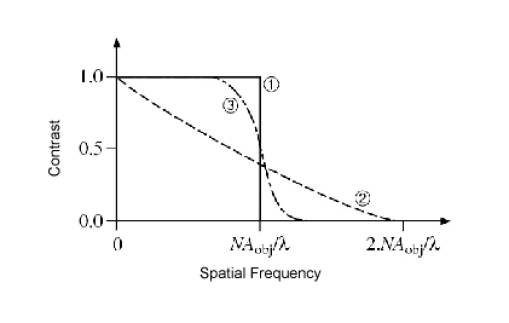
Conversely, if the aperture diaphragm is wide open so that the illumination numerical aperture is larger than the objective numerical aperture, then the illumination is said to be totally incoherent. The Fourier formalism can then be applied to the wave intensity (modulus squared of the complex amplitude). An optical system without aberration is then a low-pass filter whose transfer function gradually decays from \(1\) to \(0\) when the frequency increases from \(0\) to \(NA_{obj}\) (see Fig. 10, trace 2). The cutoff frequency is twice as large as the one obtained in the case of a coherent illumination. However, for a periodic object, the higher the spatial frequency and the smaller the contrast after transmission though the optical system.

For intermediate cases, the illumination is said to be partially coherent (See reference [ ^[2]] ), and it is not possible anymore to rigorously define a transfer function, since the system is no longer linear. However, one can obtain a good idea of the effect that will have the optical system on the image by determining the contrast of a sinusoidal test pattern as a function of its spatial frequency (See Fig. 10, trace 3). One can notice that the contrast remains equal to \(1\) for all frequencies smaller than \((NA_{obj} - NA_{ill} ) / \lambda\) and then gradually decays to reach 0 at frequency \((NA_{obj} + NA_{ill} ) / \lambda\), where \(NA_{ill}\) is the illumination numerical aperture, determined by the setting of the condenser aperture diaphragm; reference [ ^[3]] presents a clever demonstration of that property. Almost all microscopy observations are made in those illumination conditions. Indeed, they give an image containing high spatial frequencies, and with very well contrasted low and medium frequency components, which satisfies the observer subjective sense of vision. The optimal value of the illumination numerical aperture has to be adjusted for every object (and observer), and is empirically on the order of two thirds of the objective numerical aperture.

To verify the influence of the illumination coherence on image formation, it is interesting to observe diatoms preparation tests. Diatoms form a very vast and diverse family of microscopic aquatic animals, and their skeletons are made of very fine periodical structures with patterns of dimensions ranging between \(\sim 2~\mu m\) and \(\sim 0,25~\mu m\) (depending on the species). These 'objects' are therefore particularly well adapted to directly discover the microscope objective resolution limit.