Miroirs sphériques
Un miroir sphérique est une surface réfléchissante concave ou convexe définie par son centre de courbure \(C\) et un sommet \(S\) situé sur la surface. Le rayon de courbure est \(R = \overline{SC}\)
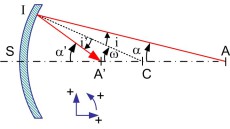
Considérons un point \(A\) de la droite \(SC\). Un rayon lumineux issu de \(A\) se réfléchit en un point \(I\) du miroir et coupe la droite \(SC\) en \(A'\). En effectuant le même calcul et le même raisonnement que pour les dioptres, nous avons :
\(\frac{\overline{CA}}{\sin (i)} = - \frac{\overline{IA}}{\sin (\omega)}\)
et
\(\overline{FA} = z-f\)
or \(\sin(i) = - \sin(i ')\) donc :
\(\frac{\overline{CA}}{\overline{CA'}} = \frac{\overline{IA} \cdot \sin (i) }{\overline{iA'} \cdot \sin (i')} = - \frac{\overline{IA}}{\overline{IA'}}\)
L'expression ci-dessus est analogue à celle des dioptres (7) en remplaçant \(n'\) par \(–n\). Nous avons donc, comme pour le dioptre, \(\overline{SA} = z ~~~~ \overline{SA'} = z' ~~~~ \overline{SC} = R\) :
\(\frac{1}{z'} + \frac{1}{z} = \frac{2}{R} \mbox{ (17)}\)
\(\;\)
\(g_{y} = \frac{\overline{A'B'}}{\overline{AB}} = \frac{y'}{y} = - \frac{z'}{z} \mbox{ (18)}\)
\(\;\)
\(g_{\alpha} = \frac{\alpha '}{\alpha} = \frac{z}{z'}\)
math : inchangé
\(\;\)
\(g_{z} = \frac{dz'}{dz} = - \frac{z'^{2}}{z^{2}} \mbox{ (19)}\)
math : toujours négatif
\(\;\)
Ces formules sont identiques que le miroir soit concave ou convexe.
La formule de conjugaison est symétrique en \(z\) et \(z'\). Si \(A'\) est image de \(A\), \(A\) est image de \(A'\).