
EVALUATION NON DESTRUCTIVE ET CONTROLE NON DESTRUCTIF PAR ULTRASONS DES MATERIAUX COMPOSITES ANISOTROPES


|
EVALUATION NON DESTRUCTIVE ET CONTROLE NON DESTRUCTIF PAR ULTRASONS DES MATERIAUX COMPOSITES ANISOTROPES |
 |
Travaux
réalisés au
Laboratoire Roberval de l'Université de Technologie de
Compiègne, ou en collaboration avec ce laboratoire. Université de Technologie de Compiègne (UTC) |
|
 |
 |
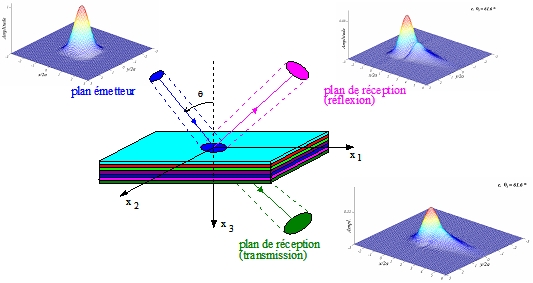 |
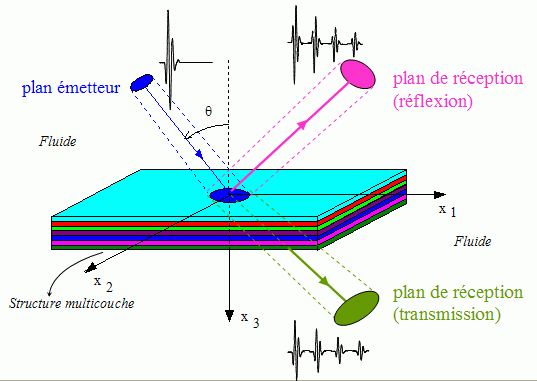
Afin de
modéliser correctement la nature
bornée
des transducteurs,
le modèle de propagation en
ondes planes
dans des
multicouches
anisotropes a été étendu aux faisceaux
bornés
Lorsque l'axe
acoustique du transducteur et sa fréquence nominale sont
tels que le
faisceau incident, de par sa nature bornée, va donner
naissance à un faisceau d'ondes modales (ondes de Lamb ou de Rayleigh
par exemple) dans
la structure, ce faisceau rayonne ensuite dans le milieu environnant.
En raison de l'anisotropie
du matériau, la direction du
faisceau borné d'ondes modales va subir une
déviation par rapport au plan
sagittal du faisceau borné incident, et, suivant le mode
choisi, peut être dévié
préférentiellement dans la direction des fibres.
Pour en savoir
plus...
|
|
|
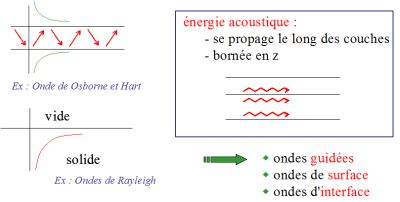 Fig. 1 Fig. 1 |
Une onde
modale [voir W.D.
Hayes, "Conservation of action and modal wave action", Proc. Roy.
Soc. Lond. A., 320,
187-208, (1970)] est
une onde pour laquelle l'énergie acoustique se propage le
long
des couches, tandis qu'elle reste bornée dans la direction
(z)
perpendiculaire aux couches (ondes guidées, ondes de
surface,
ondes d'interface).
Les ondes modales nécessitent une ou plusieurs frontières pour se construire : l'énergie acoustique se propage dans la direction d'un sous-espace de l'espace physique, tandis que ces ondes présentent un caractère stationnaire dans le sous-espace supplémentaire (au sens de la théorie des espaces vectoriels). |
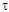 d'ordre
2 de la forme
d'ordre
2 de la forme 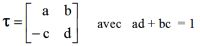 .
.
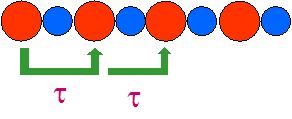 Chaîne diatomique
périodique d'atomes
|
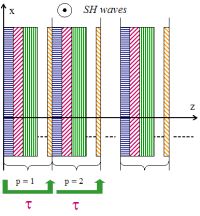 Ondes SH dans des couches isotropes |
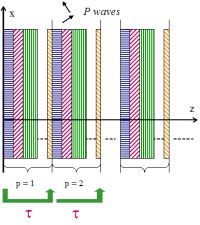 Ondes longitudinales dans des couches fluides |
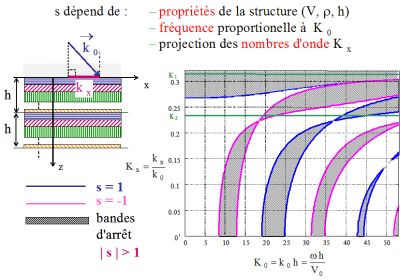 Fig. 2 Fig. 2 |
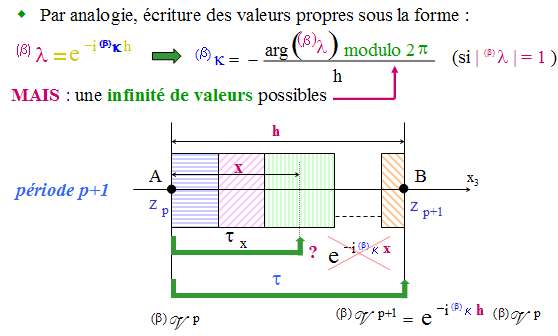
Les ondes
de Floquet qui se propagent dans une structure
périodique sont liées aux valeurs propres
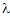 (et aux
vecteurs propres) de la matrice de transfert (et aux
vecteurs propres) de la matrice de transfert 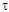 , qui sont solutions de l'équation
caractéristique , qui sont solutions de l'équation
caractéristique 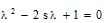 avec s=(a+d)/2.
Quand avec s=(a+d)/2.
Quand 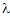 est complexe (module égal à 1), l'onde de Floquet
associée est propagative, alors qu'elle est
évanescent
lorsque
est complexe (module égal à 1), l'onde de Floquet
associée est propagative, alors qu'elle est
évanescent
lorsque 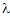 est réel.
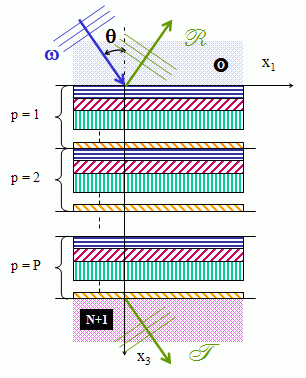
est réel. Quand les ondes de Floquet sont évanescentes, le domaine correspondant dans le plan fréquence/angle (K0,Kx) est appelé bande d'arrêt. Lorsque les ondes de Floquet sont propagatives, le domaine correspondant est appelé bande passante. Ces noms correspondent au fait que, pour une structure périodique infinie, l'énergie acoustique est totalement réfléchie dans le milieu externe pour les bandes d'arrêt, alors que pour les bandes passantes, une partie de l'énergie pénètre dans la structure périodique semi-infinie, et rayonne à l'infini. Les bandes d'arrêt et les bandes passantes de la structure correspondent respectivement aux cas |s|>1 et |s|<1. Ces zones sont séparées dans le plan (K0,Kx) par les courbes s(K0,Kx)=+1 or s(K0,Kx)=-1 (voir Fig. 2 dans le cas d'un milieu comportant 2 couches dans une période). |
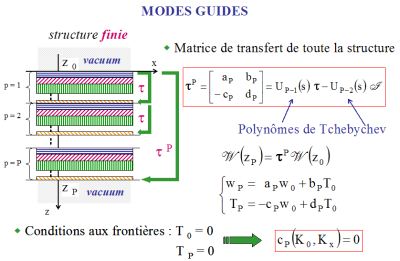 Fig. 3 Fig. 3 |
Modes
guidés
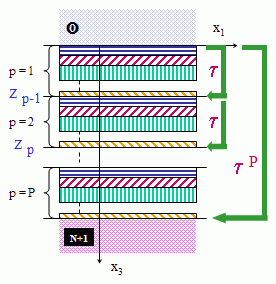
Milieu multicouche périodique constitué de P périodes (voir Fig. 3). La matrice de transfert 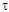 P de toute la structure peut être
calculée en fonction de P de toute la structure peut être
calculée en fonction de 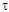 ,
en faisant usage du théorème de
Cayleigh-Hamilton, au
moyen des polynômes de Tchebychev de seconde
espèce Up(s) : ,
en faisant usage du théorème de
Cayleigh-Hamilton, au
moyen des polynômes de Tchebychev de seconde
espèce Up(s) :
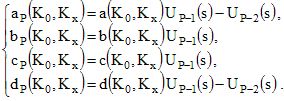
Si
la structure périodique finie est dans le vide, les
conditions
aux frontières aux interfaces extrêmes impliquent
l'annulation des contraintes (TP=0 et T0=0),
ce qui conduit à une équation
aux modes propres factorisée :
cP(K0,Kx)=0 c'est-à-dire
c(K0,Kx)
UP-1(s)=0 , ce qui conduit
à deux
familles d'ondes modales.
|
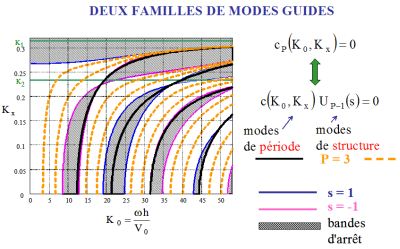 Fig. 4 Fig. 4 |
- La première famille d'ondes modales
correspond à ce qui peut être appelé
des ondes
modales de structure. Elles sont données
par la condition UP-1(s)=0. A partir des propriétés
des polynômes de Tchebychev, les (P-1)
racines de cette condition sont telles que |s|<1,
ce qui revient à dire que ces modes existent dans les bandes
passantes.
Pour le milieu fluide périodique de la Fig. 4 avec P=3
périodes, on peut voir qu'il y a 2 modes de structure dans
chaque bande passante (traits pointillés orange).
- La seconde famille d'ondes modales correspond
à ce qui peut être appelé des ondes
modales de période. Elles sont
données par la condition c(K0,Kx)=0,
qui est indépendante du nombre P de périodes, et
qui
correspond donc à des ondes modales qui sont directement
liées au motif de période, et qui sont telles
que |s|>=1. Par suite, les modes de périodes
sont localisés dans les bandes
d'arrêt ou sur leurs frontières (voir
Fig. 4, trait continu noir).
|
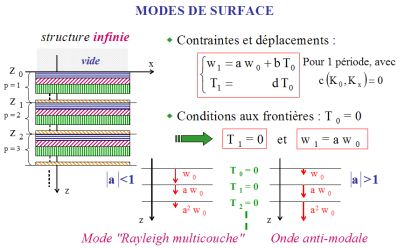 Fig. 5 Fig. 5 |
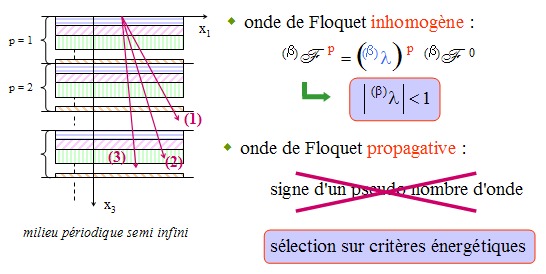
Ondes
modales de surface dans une structure semi-infinie, l'interface
supérieure étant en contact avec le vide -
Une telle onde modale de surface peut exister dans une structure fluide
périodique semi-infinie, alors qu'elle ne peut pas exister
dans
un simple milieu fluide.
- Sous la condition c(K0,Kx)=0, quand la première interface de la
structure est en contact avec le vide, la condtion T0=0
implique la condition T1=0
et
ainsi de suite pour les autres interfaces de période. En
particulier, après p périodes, le
déplacement
normal est tel que wp=ap
w0.
- Puisque la structure est semi-infinie, l'entier p augmente indéfiniment à mesure que z tend vers l'infini. Par suite, si |a|<1 alors l'amplitude de l'onde, observée à chaque interface de période, va décroître en fonction de z, alors que si |a|>1 elle va augmenter (voir Fig. 5). |
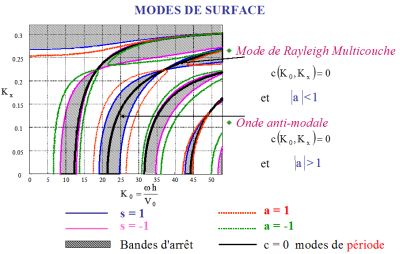 Fig. 6 Fig. 6 |
- Le premier cas correspond à une onde modale de surface (ce qui a été appelé une "onde de Rayleigh multicouche"). - Le second cas correspond à ce qui
peut être appelé une "onde
anti-modale" : une telle solution modale a peu de sens
physique, puisque son amplitude n'est pas bornée
à l'infini.
- Il convient de noter le rôle crucial joué ici par le caractère périodique de la structure : en fait, dans le cas des milieux fluides homogènes semi-infinis, il n'y a pas d'onde modale de surface similaire à ce qui vient d'être décrit pour une structure périodique. - Lorsque les couches sont empilées en ordre inverse, l'onde modale de surface et "l'onde anti-modale" sont échangées. |
|
Conditions aux
frontières
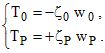 |
Equation aux modes propres
(équation de dispersion) :
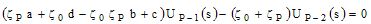 |
|
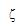 0 + 0 +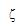 P = 0 : P = 0 : équation
aux modes propres factorisée
|
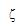 0 = 0 =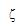 P : équation
aux modes propres non
factorisée P : équation
aux modes propres non
factorisée |
|
| Mur rigide: Zw
tend vers l'infini ou vide : Zw = 0 |
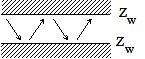 |
|
| Pure impédance reactive | 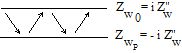 |
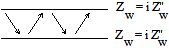 |
| Ondes propagatives dans le même milieu fluide externe |
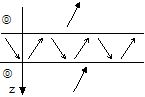 Transmission totale |
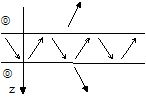 Ondes modales généralisées (kx n'est pas réel) |
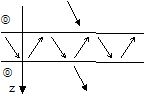 Transmission totale |
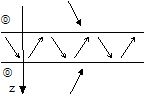 Ondes anti-modales généralisées (kx n'est pas réell) |
|
| Ondes évanescentes dans le même milieu fluide externe |
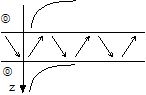 Ondes anti-modales |
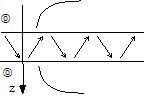 Ondes anti-modales |
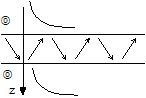 Ondes anti-modales |
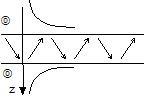 Ondes de Osborne et Hart |
|

|
Une poutre pultrudée en verre/époxyde comprenant 3 couches de mat et 2 couches de roving a été impactée (contact : Thierry Chotard) |
|
|
Une cartographie ultrasonore C-Scan à différentes hauteurs permet de retrouver des résultats classiques : près du point d'impact, la zone endommagée est moins large qu'au fond de la pièce. |
| En prenant en compte la réponse réelle du transducteur, on peut parfaitement simuler la réponse échographique du milieu [A6, B4] grâce au modèle en ondes planes développé. |