
Animations
 |
Animations |
 |
Modes in an infinite cylindric tube
 |
Modes in an infinite cylindrique tube
with a meridian half wall  |
| INFINITE CYLINDRIC TUBE | |
|
The acoustic field
created by a
monochromatic source in an infinite cylindric tube (diameter 2a) can be
expressed as the superposition of the fields associated to
each mode (
 ,m) : ,m) :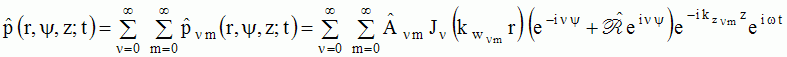  , , |
|
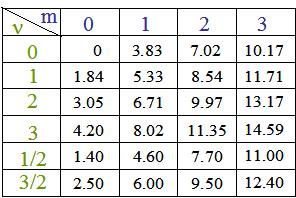
where 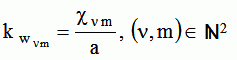 , the
numbers , the
numbers 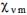 corresponding to the (m+1) zeroes of the
derivative of the Bessel function of the 1st kind J corresponding to the (m+1) zeroes of the
derivative of the Bessel function of the 1st kind J , i.e. to the (m+1) extremas of this function. , i.e. to the (m+1) extremas of this function.Thus, the acoustic
field is
propagative following the axis z of the cylinder, is stationary
following the radius r, and is either propagative or stationary
following the azimuth
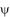 ,
according to the nature of the source. ,
according to the nature of the source. |
 |
|
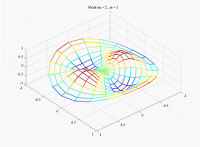
Case of
the stationary mode in
As the volume of the fluid at the interior of the cylinder permits to
bypass the Oz-axis when the azimuth 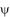 . .
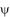 varies, the quantic number varies, the quantic number  is an integer and can be denoted n. The pressure associated to
each mode (
is an integer and can be denoted n. The pressure associated to
each mode ( ,m) is thus given by: ,m) is thus given by: 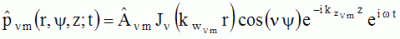 . . |
|
| The
animations below represent the variation of the acoustic pressure of
a mode (n,m) in a section of the cylindric tube, for a given
z,
with color level (red =
maximum, blue = minimum). |
|
 =0
; m=0 =0
; m=0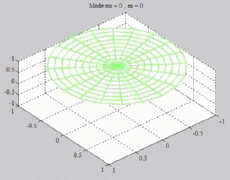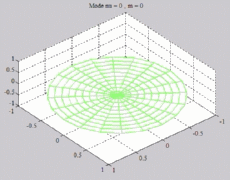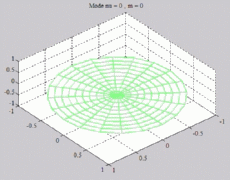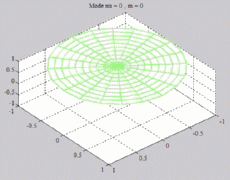 |
 =0
; m=1 =0
; m=1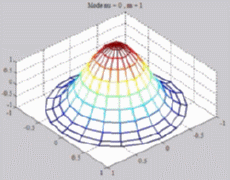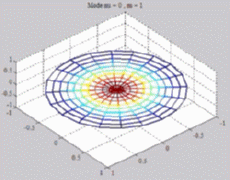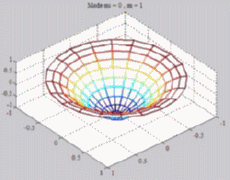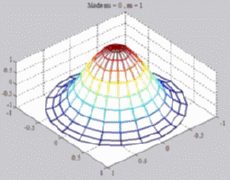 |
 =0
; m=2 =0
; m=2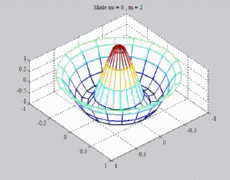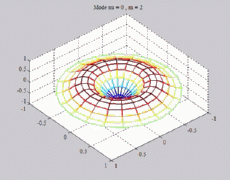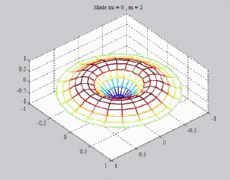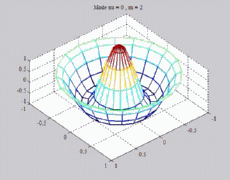 |
 =0
; m=3 =0
; m=3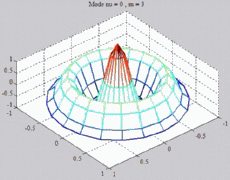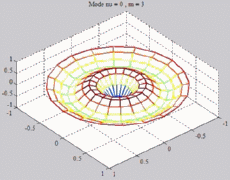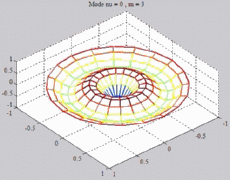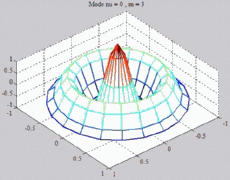 |
 =1
; m=0 =1
; m=0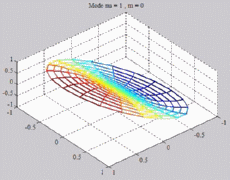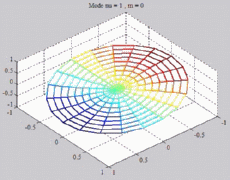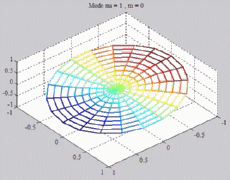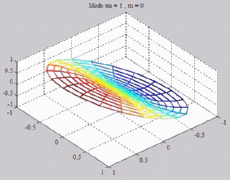 |
 =1
; m=1 =1
; m=1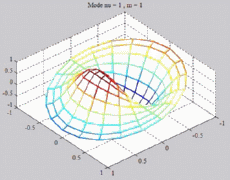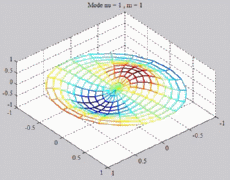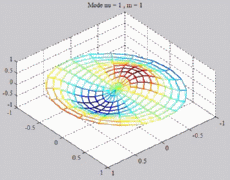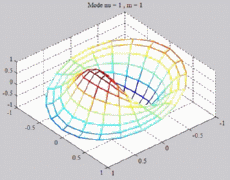 |
 =1
; m=2 =1
; m=2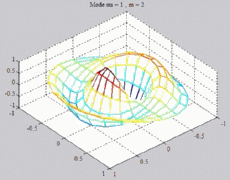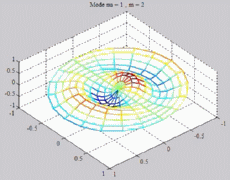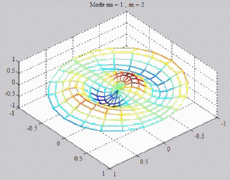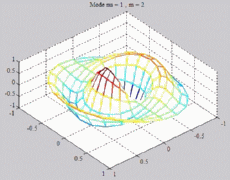 |
 =1
; m=3 =1
; m=3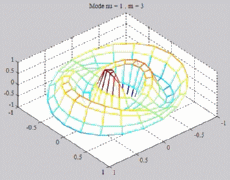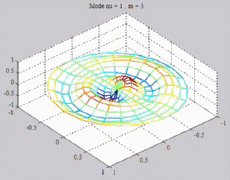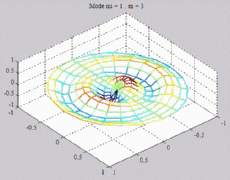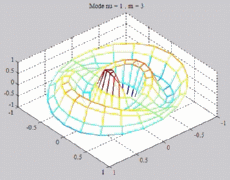 |
 =2
; m=0 =2
; m=0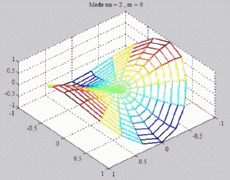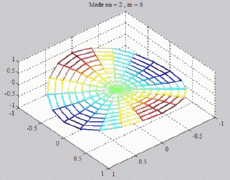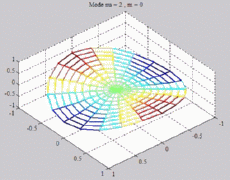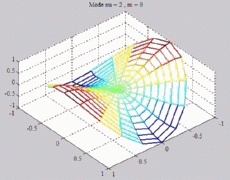 |
 =2
; m=1 =2
; m=1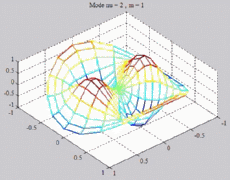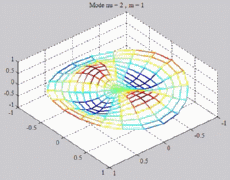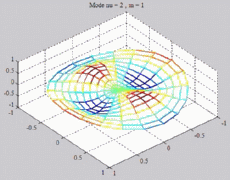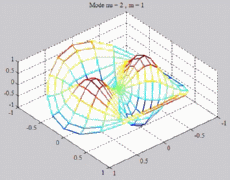 |
 =2
; m=2 =2
; m=2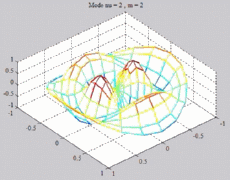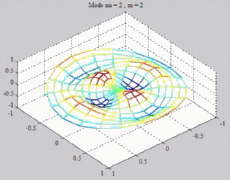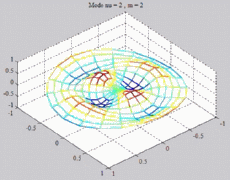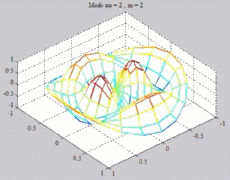 |
 =2
; m=3 =2
; m=3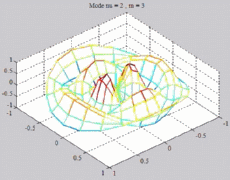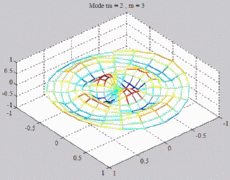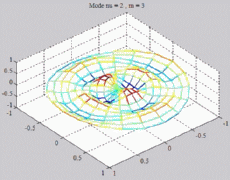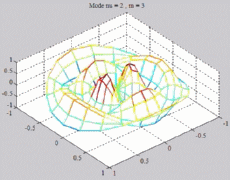 |
 =3
; m=0 =3
; m=0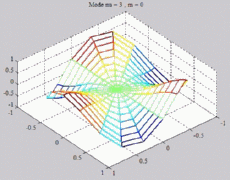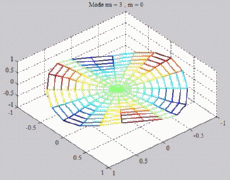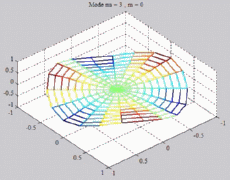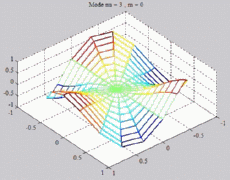 |
 =3
; m=1 =3
; m=1 |
 =3
; m=2 =3
; m=2 |
 =3
; m=3 =3
; m=3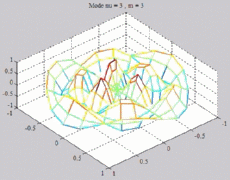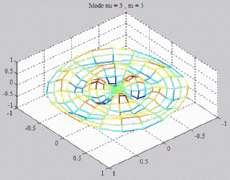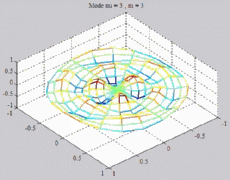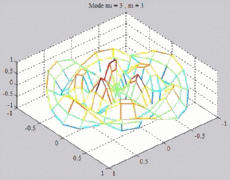 |
| INFINITE CYLINDRIC TUBE WITH A MERIDIAN HALF WALL |
|
The acoustic field
created by a monochromatic source in an infinite
cylindric tube (diameter 2a) can be expressed as the superposition of
the fields
associated to each mode (
 ,m),
with here ,m),
with here  =N/2.
Indeed, as the volume of the fluid at the interior of the cylinder does
not permit to bypass the Oz-axis when the azimuth =N/2.
Indeed, as the volume of the fluid at the interior of the cylinder does
not permit to bypass the Oz-axis when the azimuth 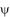 varies (due to the presence of the meridian
half wall), the quantic number varies (due to the presence of the meridian
half wall), the quantic number  is no more necessary an integer. The acoustic pressure associated to
each mode (
is no more necessary an integer. The acoustic pressure associated to
each mode ( ,m) is thus given by: ,m) is thus given by: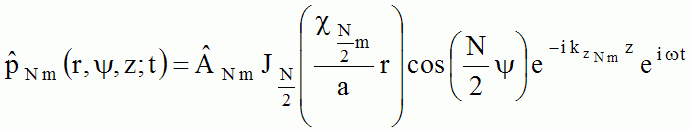  For N being an odd number, the stationary modes are anti-symmetric with respect to the meridian half wall. |
The
animations below represent the variation of the acoustic pressure of
a
mode ( ,m) in
a section of the cylindric tube, for a given z, with
color level (red =
maximum, blue = minimum). ,m) in
a section of the cylindric tube, for a given z, with
color level (red =
maximum, blue = minimum). |
 =0.5
; m=0 =0.5
; m=0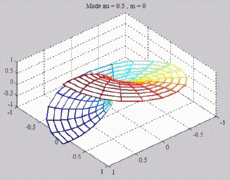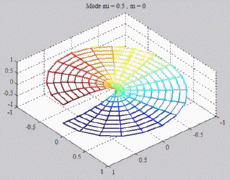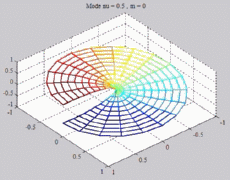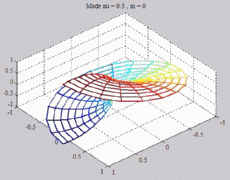 |
 =0.5
; m=1 =0.5
; m=1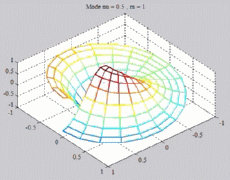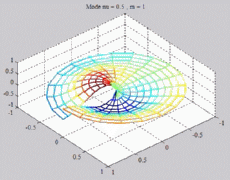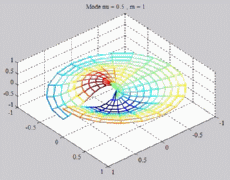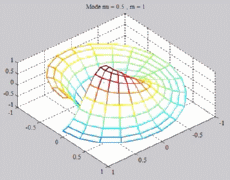 |
 =0.5
; m=2 =0.5
; m=2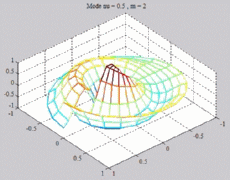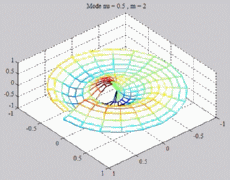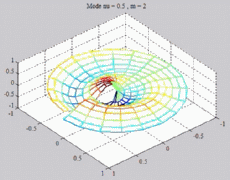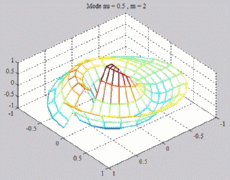 |
 =0.5
; m=3 =0.5
; m=3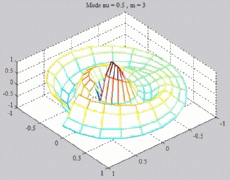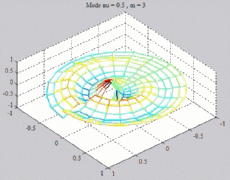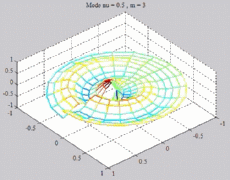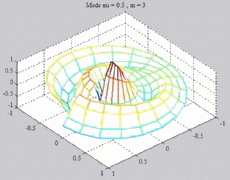 |
 =1.5
; m=0 =1.5
; m=0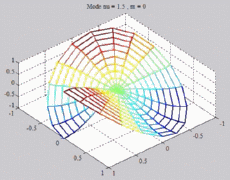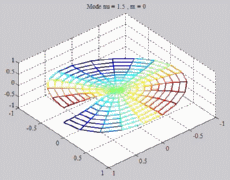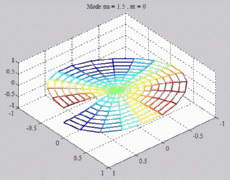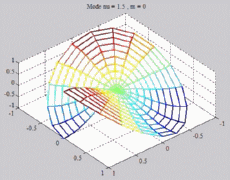 |
 =1.5
; m=1 =1.5
; m=1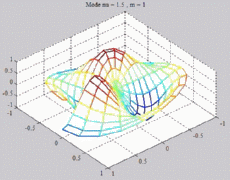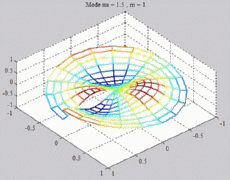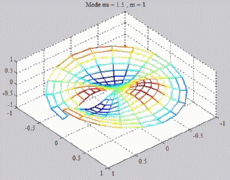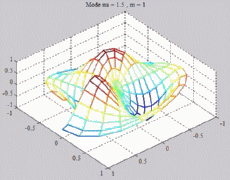 |
 =1.5
; m=2 =1.5
; m=2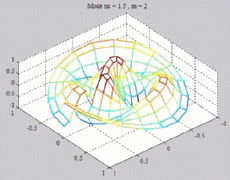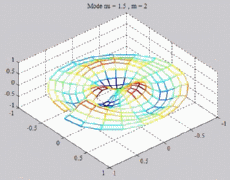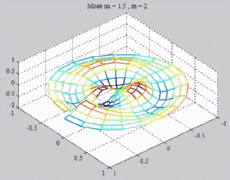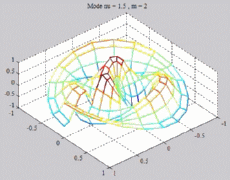 |
 =1.5
; m=3 =1.5
; m=3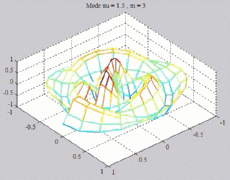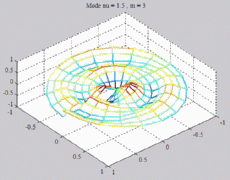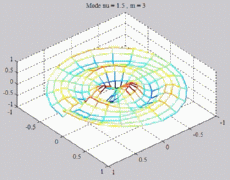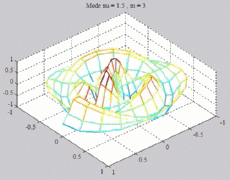 |