
Animation
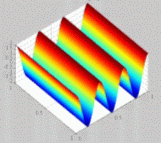
 |
Animation |
 |
|
General definition:
a stationary (standing) wave is a wave for which the associated REAL physical
quantity
(acoustic pressure, particle velocity, potential) can be written in the
form of the product of a function depending on the spatial variables x,
y, z, and of a function depending on the time t:
p(x,y,z;t) = P(x,y,z) T(t).
Generally
speaking, P(x,y,z) is
not necessarily a sinusoidal function, whereas T(t) is necessarily a
sinusoidal function. On the other hand, if P(x,y,z) can be written as
P(x,y,z) = P1(x) P2(y,z),
then P1(x) is necessarily a sinusoidal function,
whereas P2(y,z) is not necessarily a sinusoidal
function.
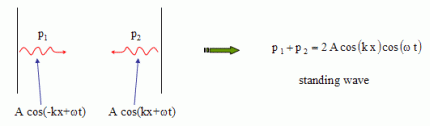
Particular case of a unidimensional problem  Here, X(x) is
necessarily a sinusoidal function (see opposite figure).
|
|
||||