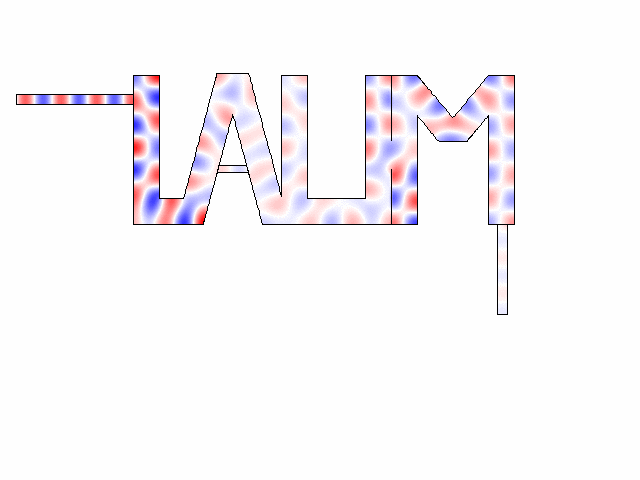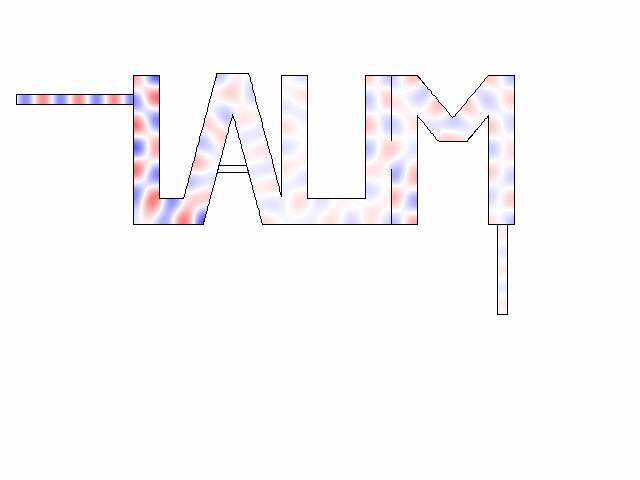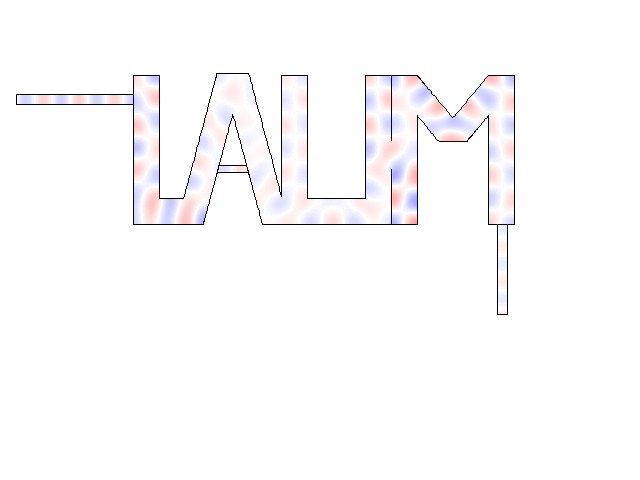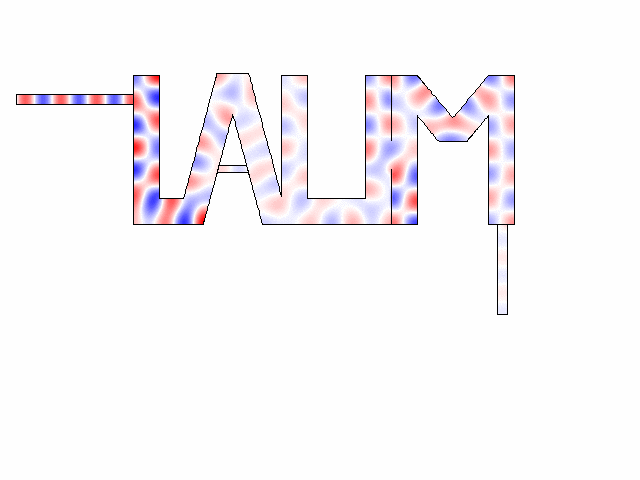





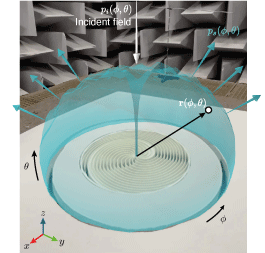


Acoustic metamaterials are characterized by their locally resonant unit cells. These resonant scatterers introduce strong dispersion in the system producing two main effects. The first one is the reduction of the slope of the dispersion relation when frequency goes to zero. The second one is a hybridization between the resonance and the dispersion line of the non dispersive host, resulting in a dispersion relation with a slope that goes to zero at the lower edge of the resonant band gap. In any case, in the first band gap the phase velocity in the metamaterial is smaller than that of the host.
In the animation we can see the difference between the speed of sound inside the metamaterial with respect to the exterior media, showing the effect known as slow waves. In the current example, the resulting system is a Fabry-Pérot resonator the resonance frequency of which is shifted down due to the slow wave phenomenon.
Losses in acoustic metamaterials are, in most of the cases, not avoidable. In this particular example we exploit the presence of losses to create perfect absorbers.
In this example we have an open lossy resonator presenting both inherent losses due to the viscothermal losses in the resonator and in the slit as well as leakage of energy due to the opening between the resonator and the exterior medium.
Perfect absorption can be obtained when the energy leakage is compensated by the inherent losses. This represents the critical coupling condition which also represents the impedance matching condition. Here we show a pure reflection problem in which the total absorption can be obtained with a single resonance.
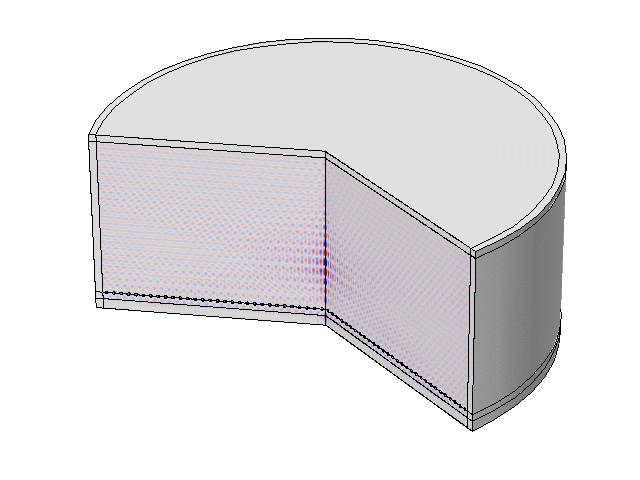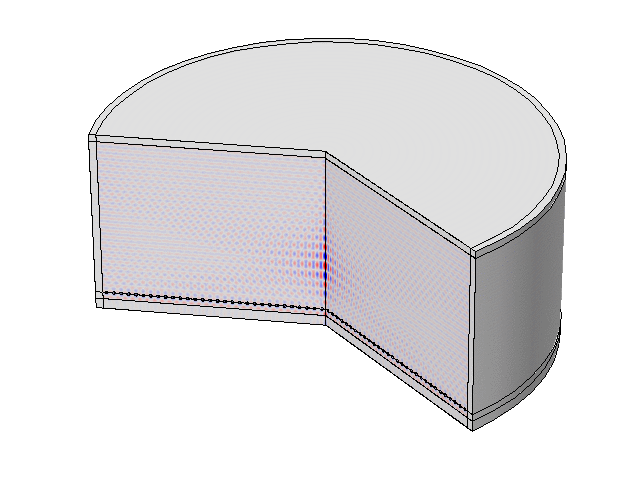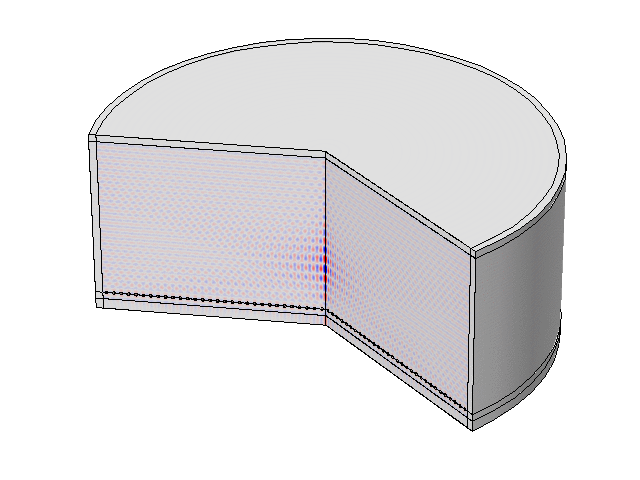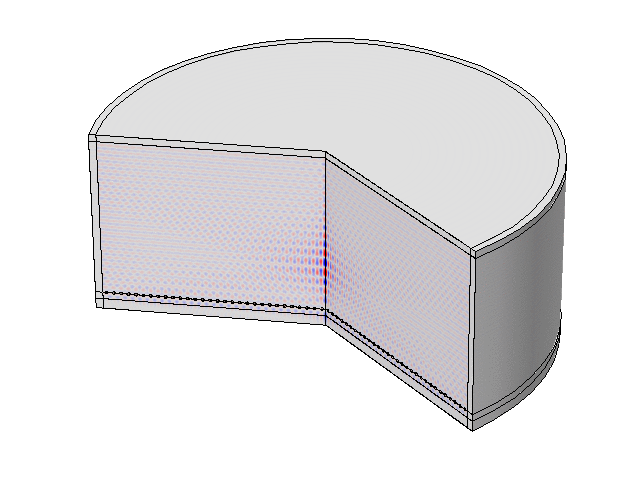
The “LAUM”- shaped medium is filled with air. A nonuniform pressure field distribution inside the 2D medium with high-order modes and a weak transmission (7%) is obtained. The pressure field is strongly dependent on the geometry of the host.
Experimental results of the absorption of flexural waves by a resonant termination with impedance mismatch. The termination produces reflections that excites standing waves in the main beam. The system is excited by a transducer from the oposite sice with a sinusoidal signal.
Experimental results of the perfect absorption of flexural waves. The termination is impedance matched and there is not standing waves in the main beam.
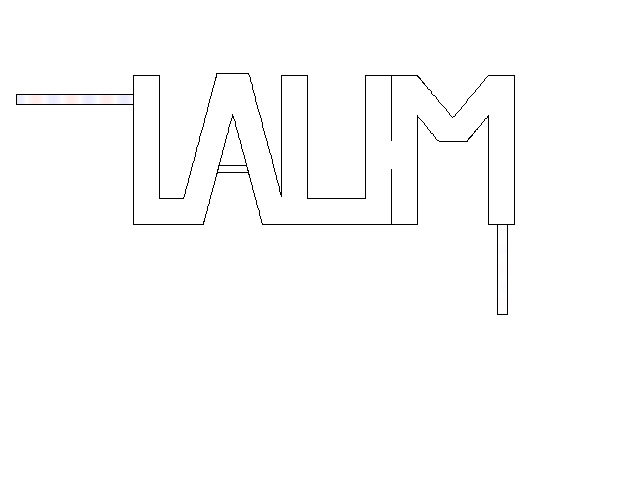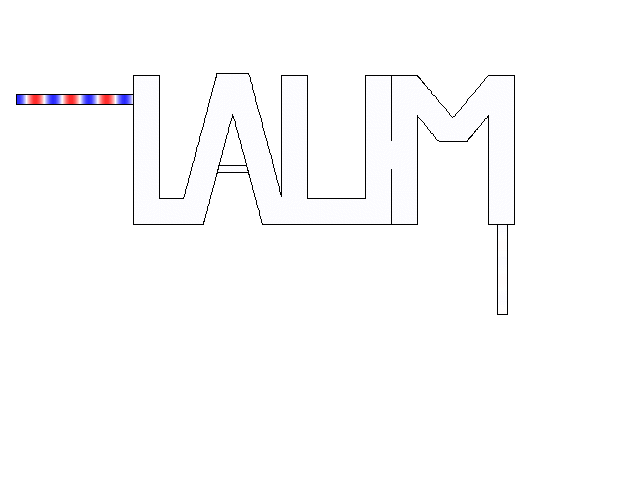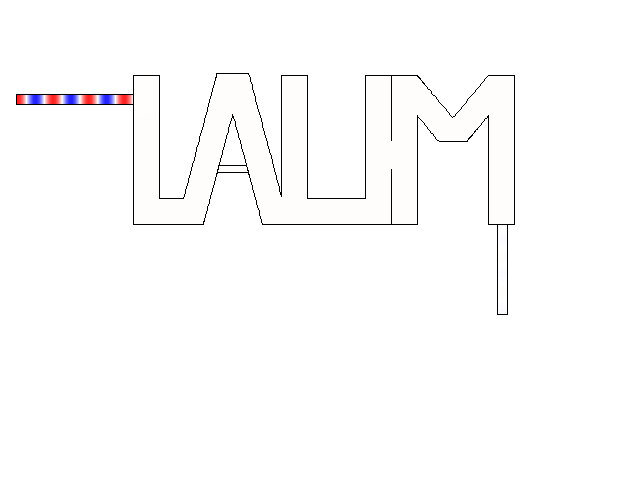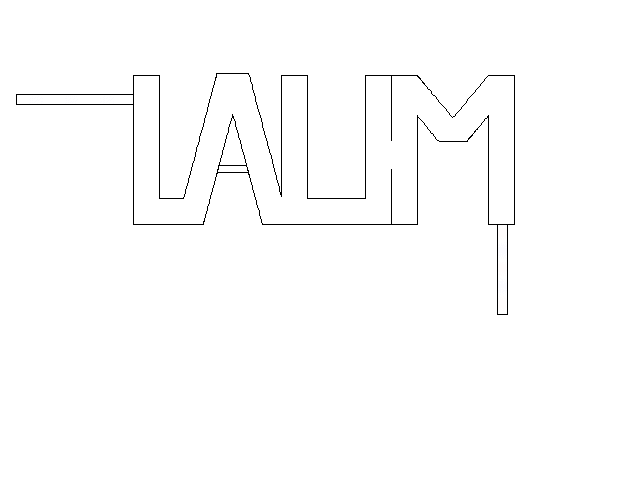



Numerical simulations about acoustic dopping with an effective medium and an acoustic metamaterial made of clampled elastic plates. A full-wave simulation of the doping phenomenon on a two-port random two-dimensional (2D) medium is performed. The input and output ports are air-filled waveguides, plugged into the “L” and “M” shapes, respectively. A monochromatic wave of frequency lower than the cut-off frequency of the ports (above which other modes than the plane wave one can propagate) impinges the structure from the left ensuring plane-wave propagation.
Source: M. Malléjac et al., Phys. Rev. B, 102, 060302(R), (2020)
The “LAUM”- shaped medium is filled with Density Near Zero material with null density at the frequency of the incident wave. The pressure field becomes uniform within the medium due to the stretching of the effective acoustic wavelength, allowing a wave propagation without phase delay. The pressure field is geometry independent. In this case, due to the impedance missmatch, the transmission is almos zero.
The “LAUM”- shaped medium is filled with Density Near Zero material with null density at the frequency of the incident wave, except the horizontal bar of the "A" letter in which a dopant with a huge value of bulk modulus is considered. The pressure field becomes uniform within the medium due to the stretching of the effective acoustic wavelength, allowing a wave propagation without phase delay. The pressure field is geometry independent. In this case, due to the impedance matching, the transmission is perfect in the lossles case.
Under construction
Under construction
Under construction
Under construction
Some pictures of experiments
Slow waves
Perfect absorption
Acoustic doping
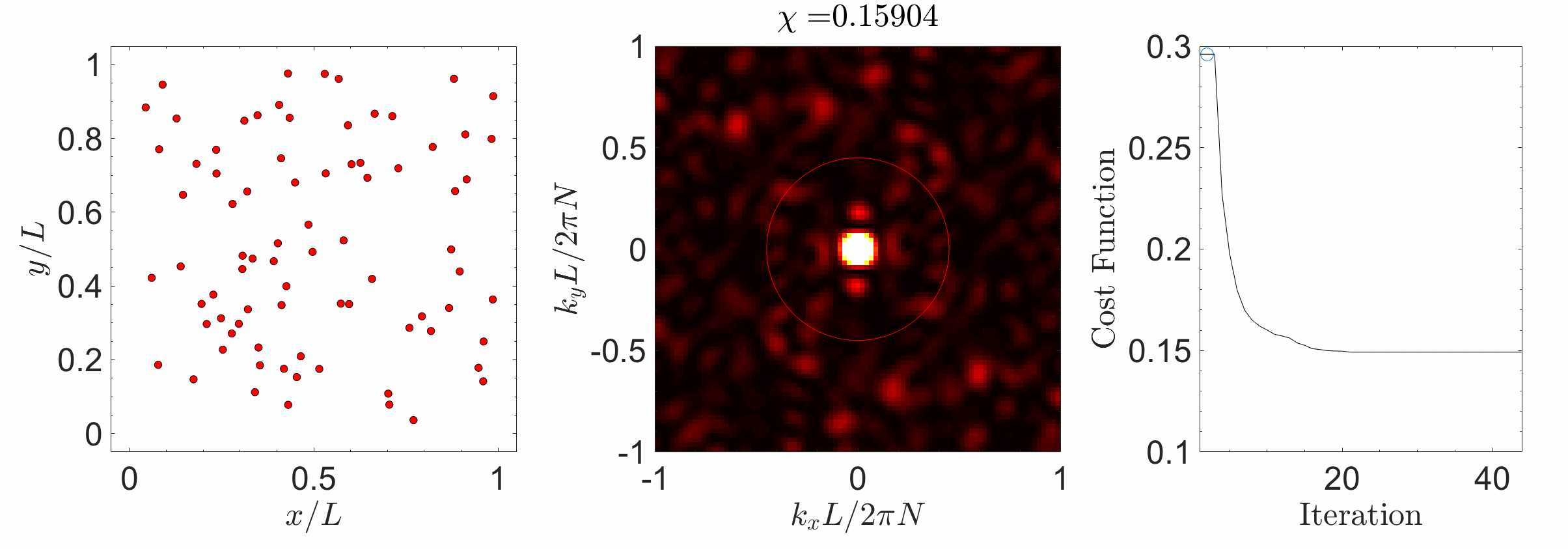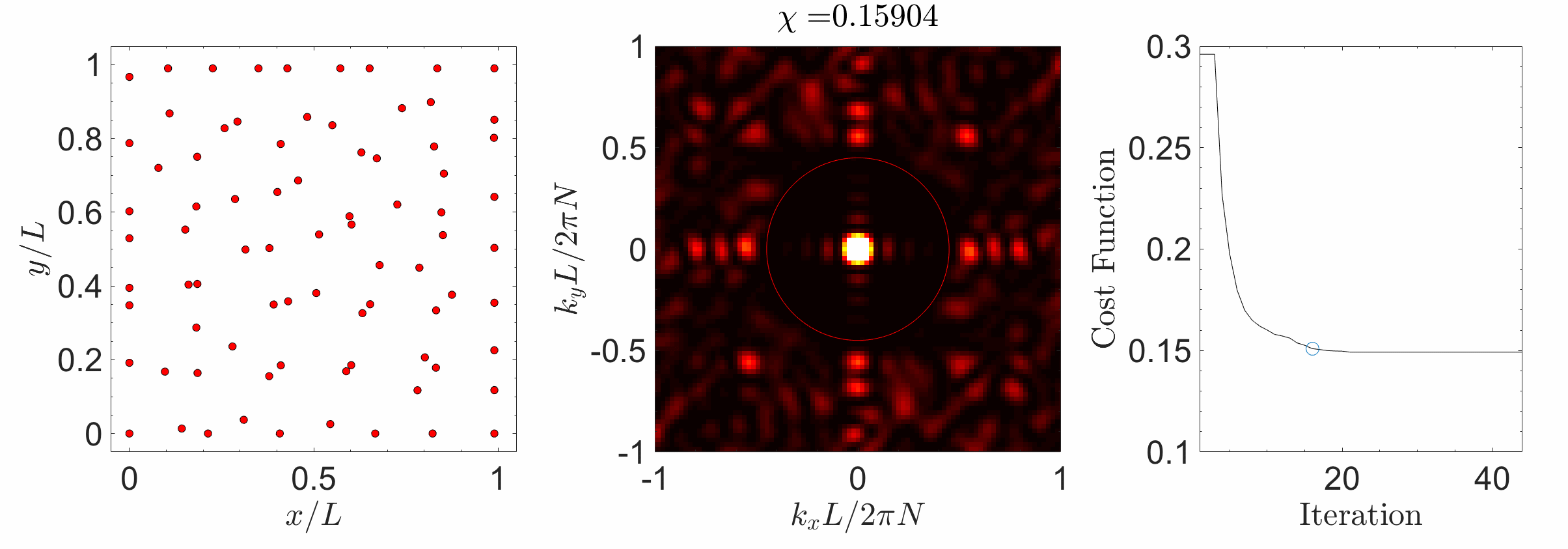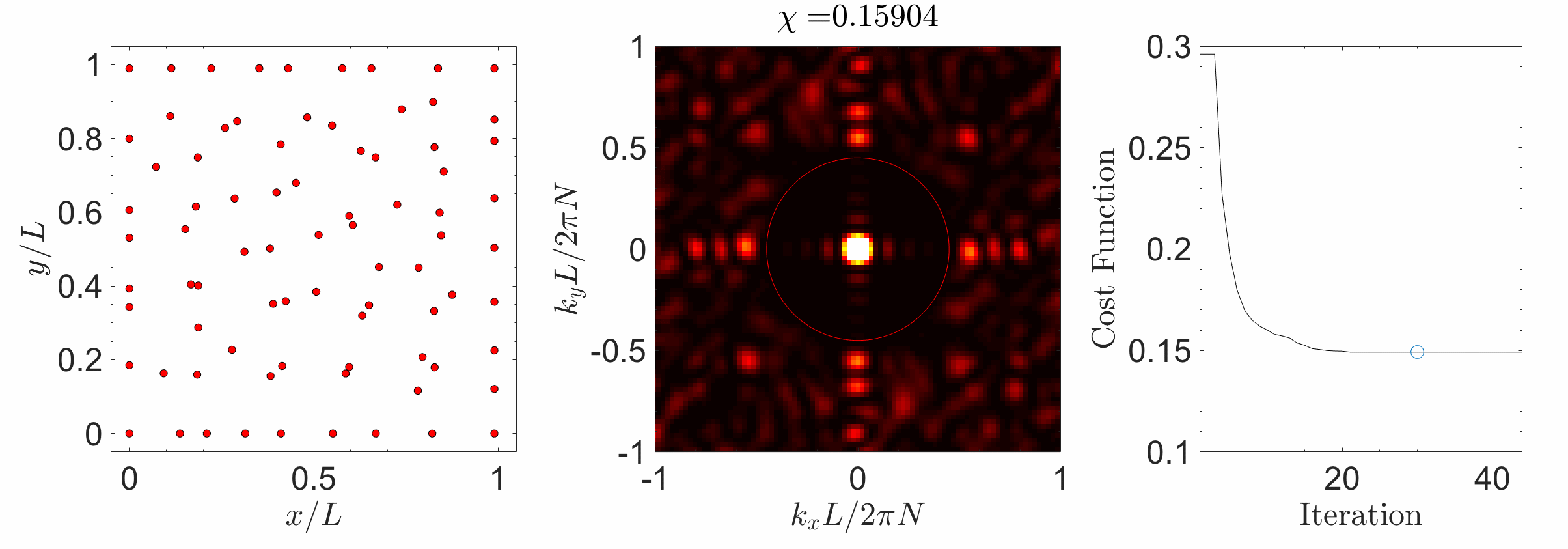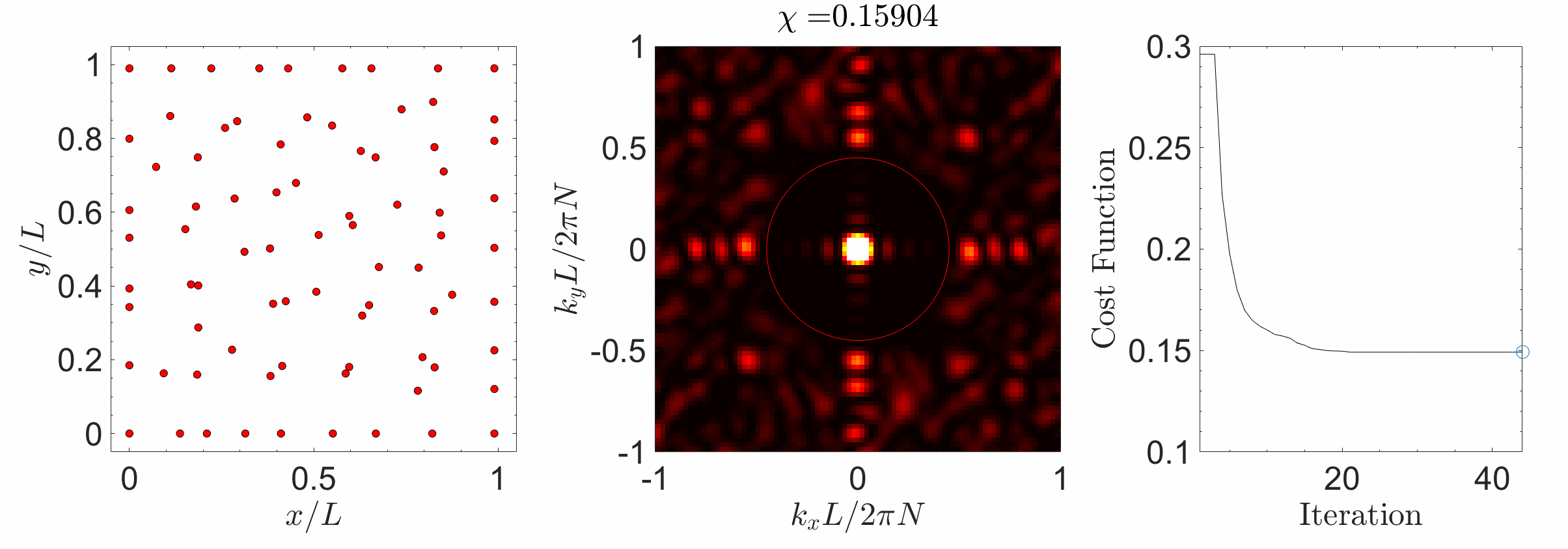
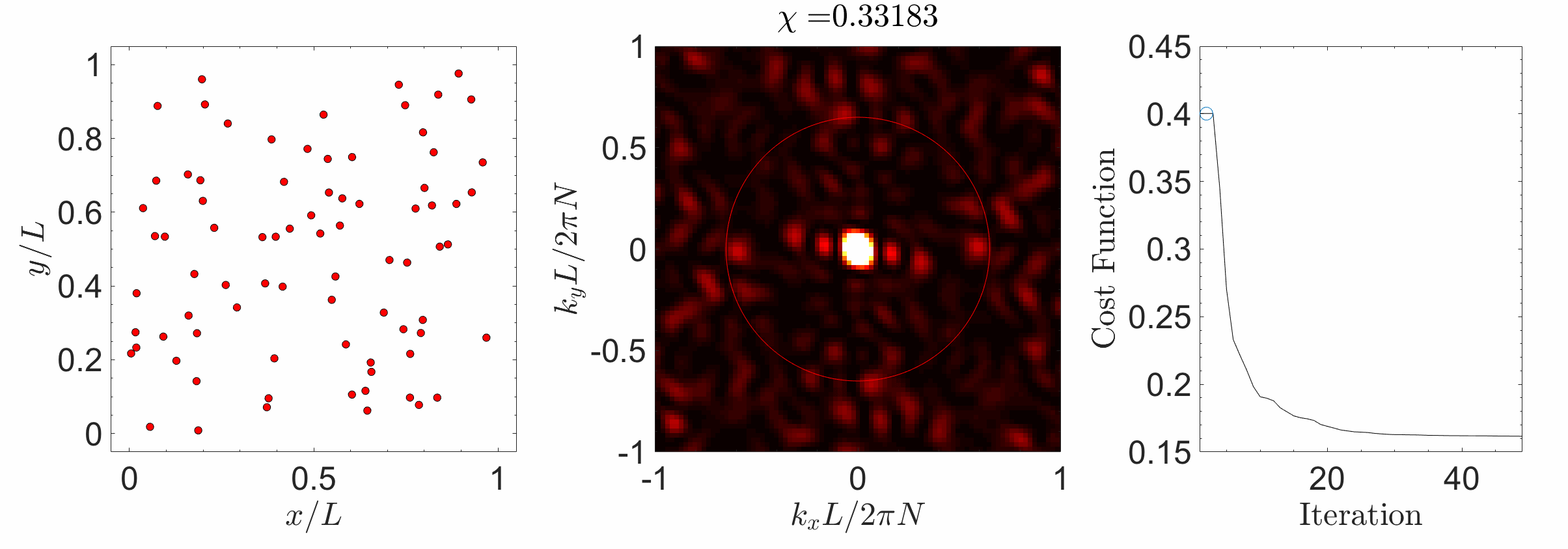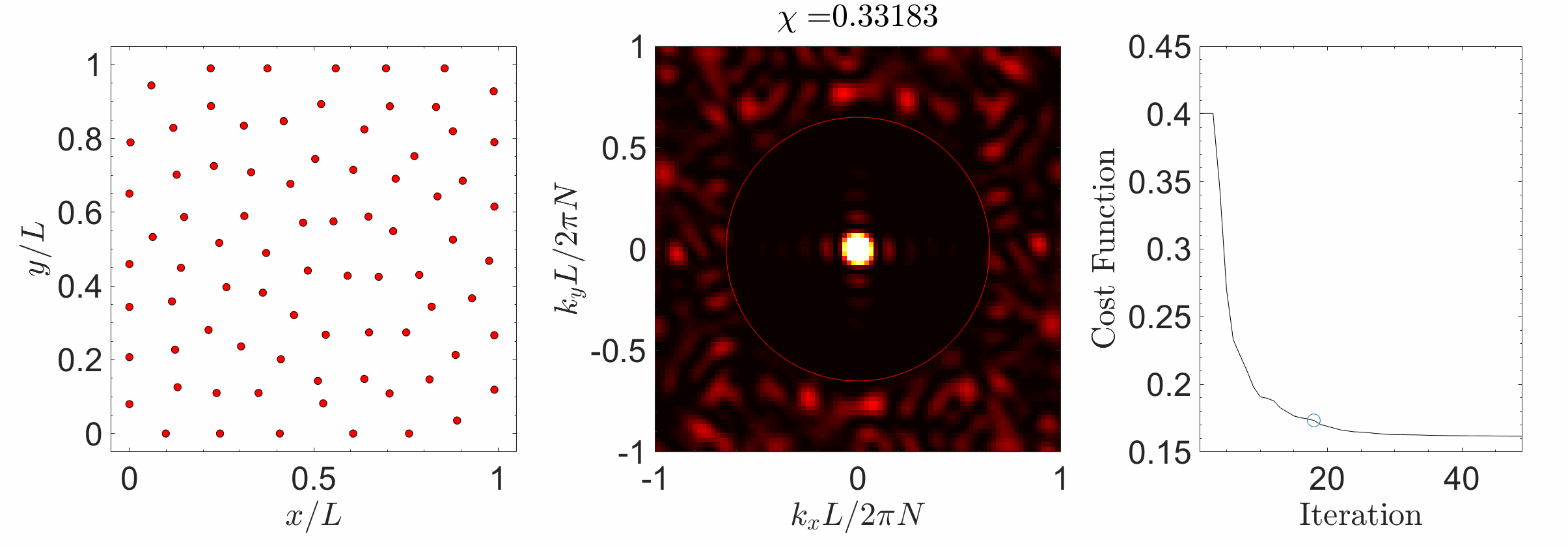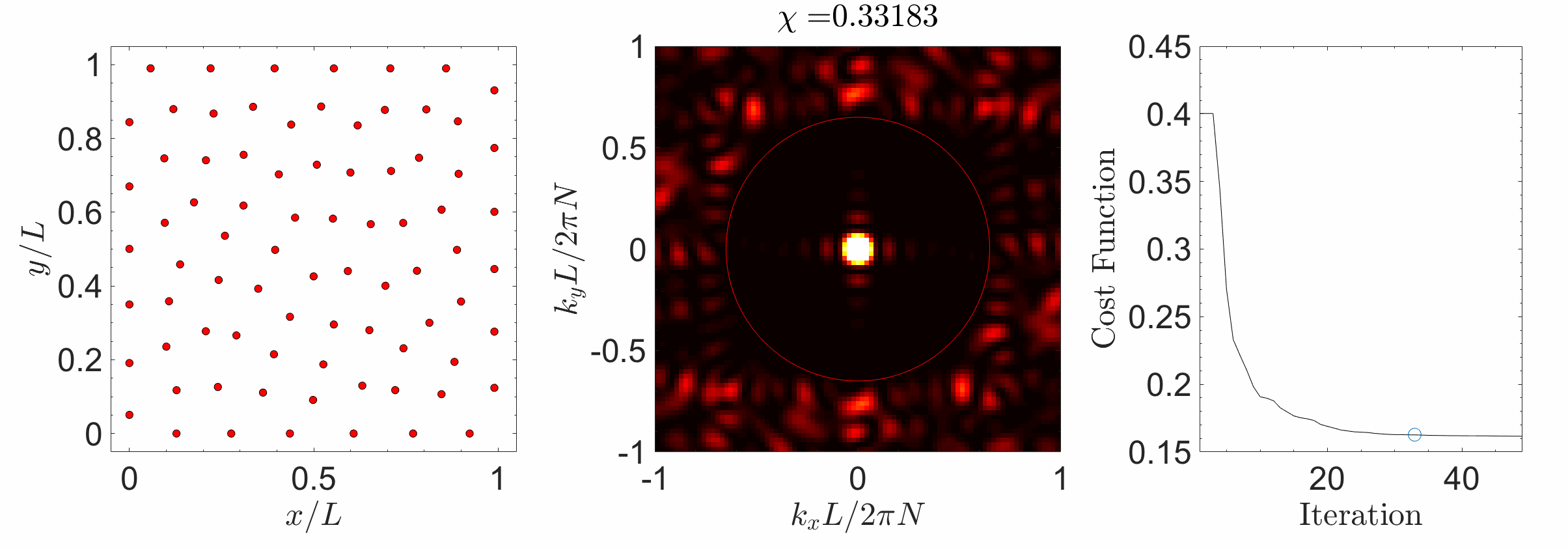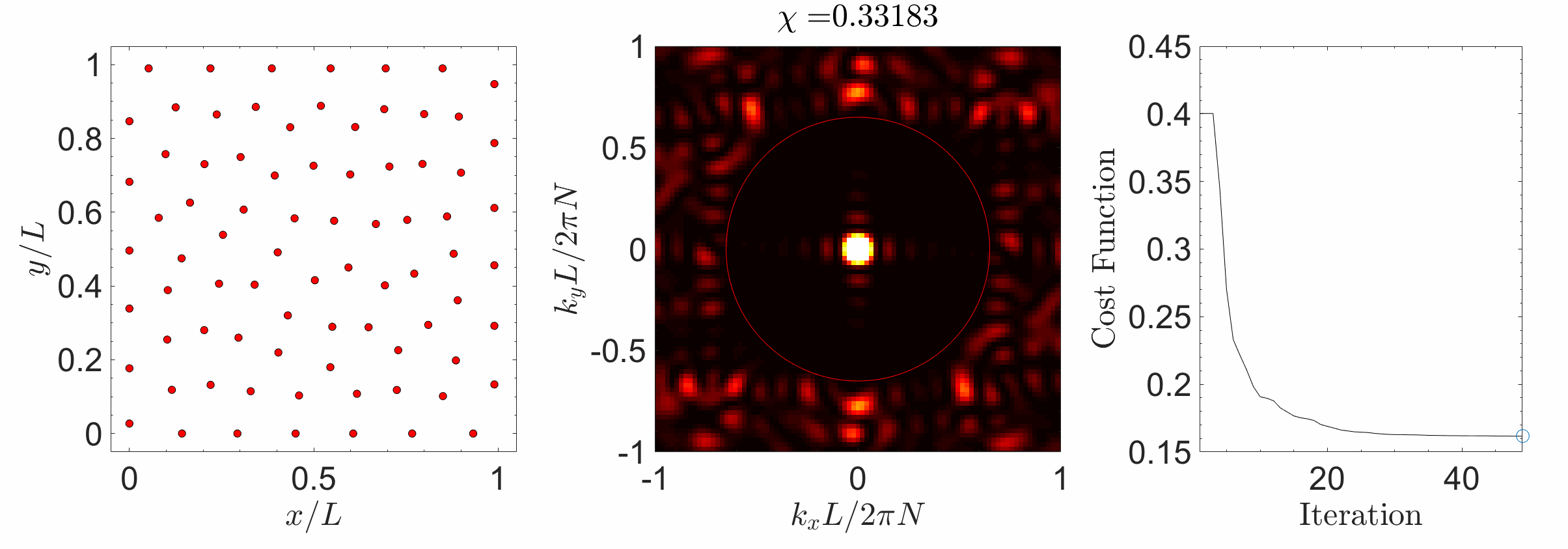
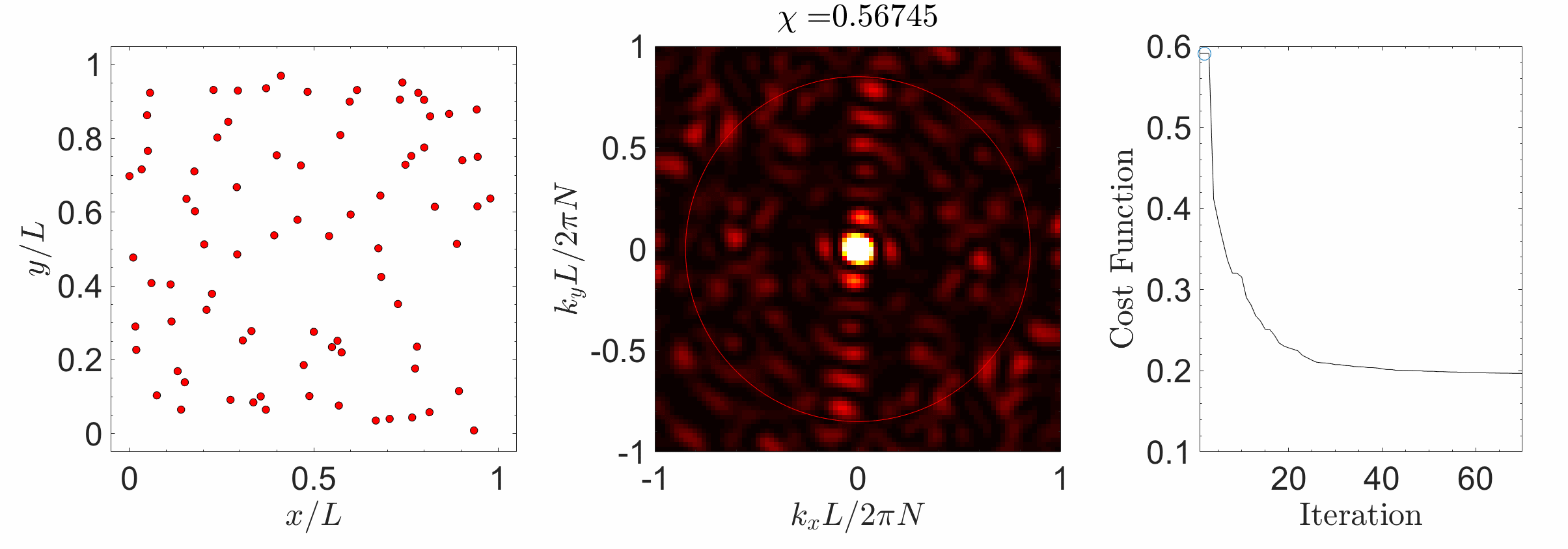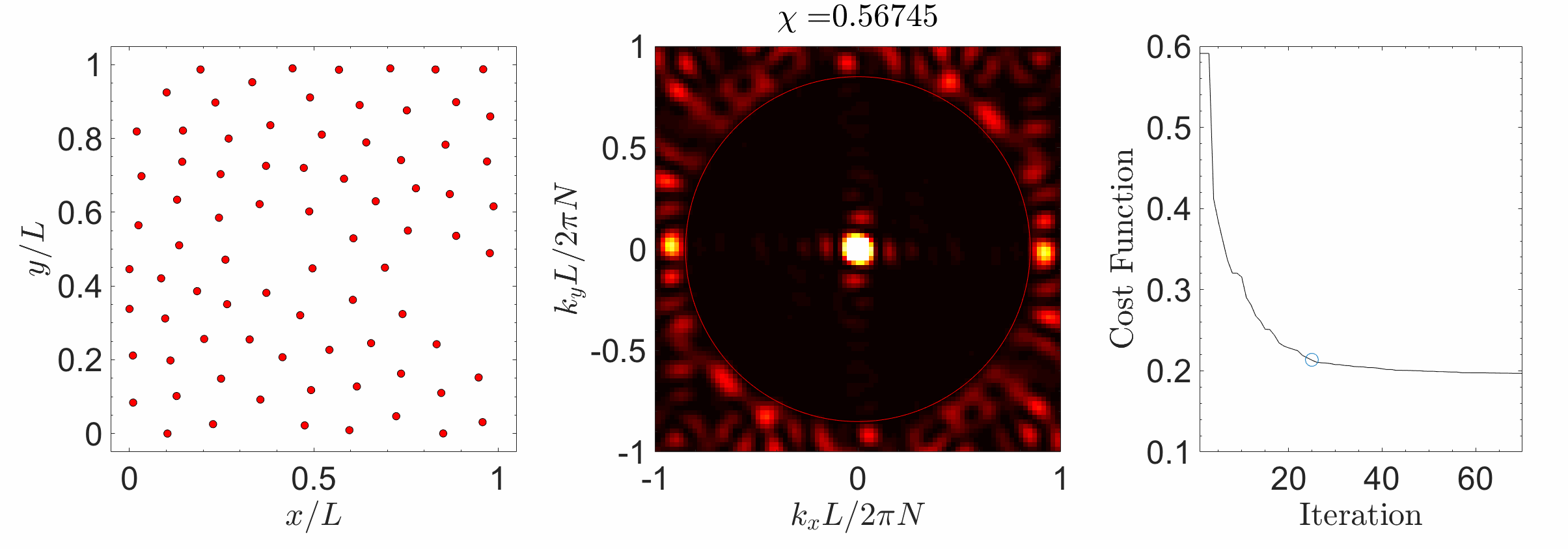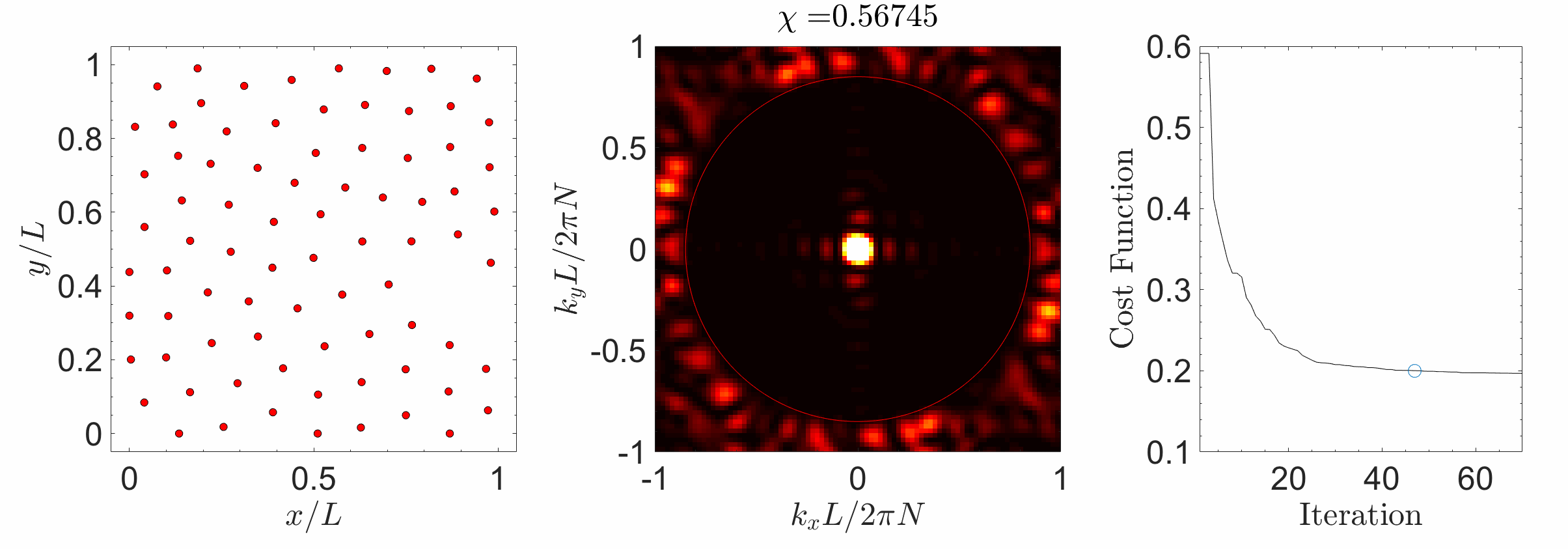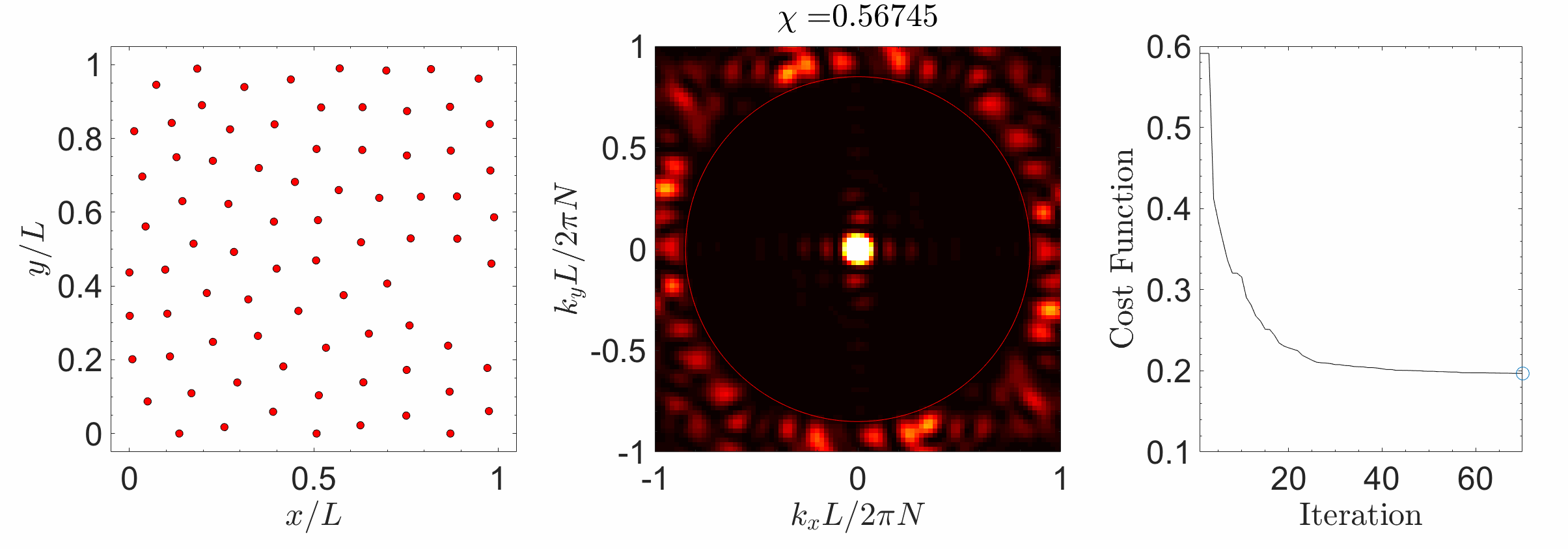
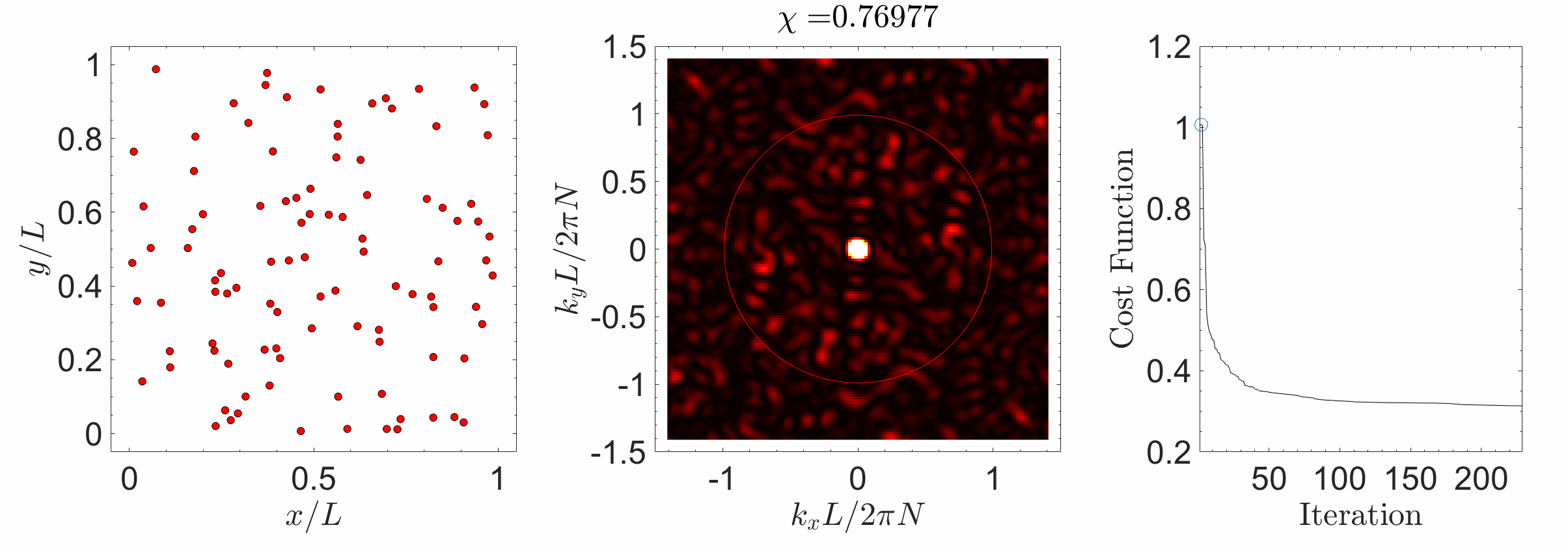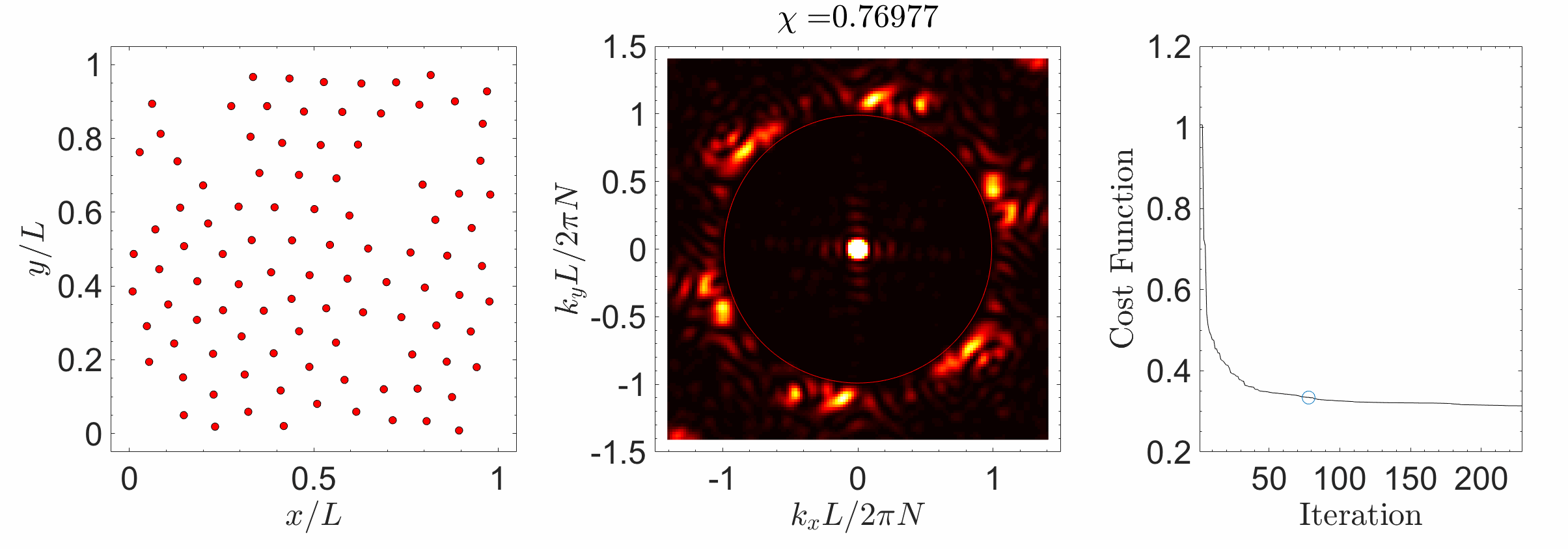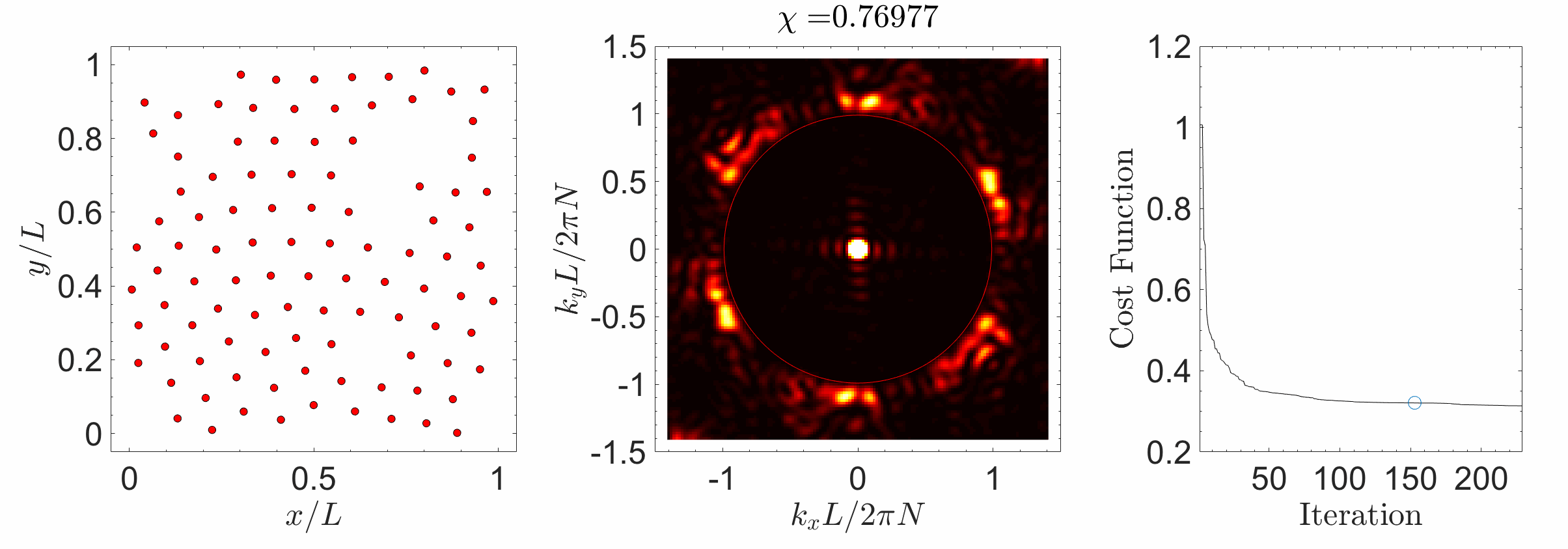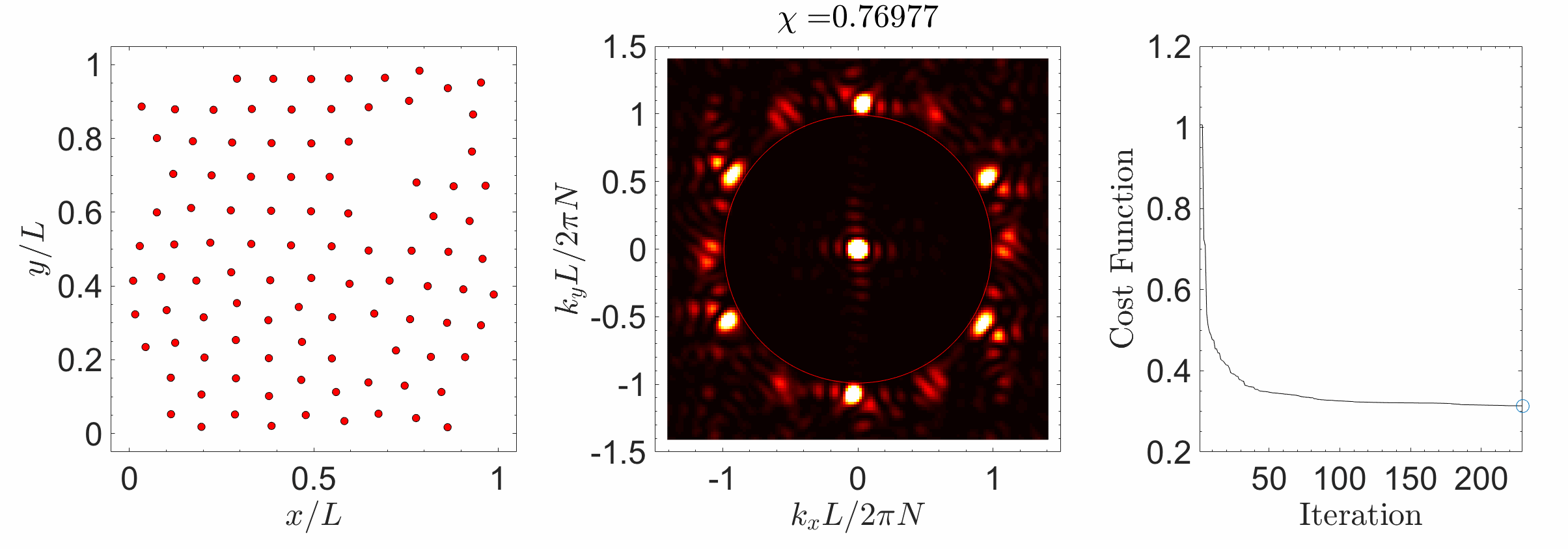
Hyperuniform materials
Bessel beams
Acoustic cloaking
Stealth materials