
PROPAGATION D'ONDES MODALES EN PRESENCE DE RUGOSITE - COUPLAGES MODAUX

 |
PROPAGATION D'ONDES MODALES EN PRESENCE DE RUGOSITE - COUPLAGES MODAUX |
 |
| En collaboration avec le Laboratoire d'Acoustique Ultrasonore et d'Electronique
(LAUE), UMR CNRS
6068, Le Havre
et l'Institut
d'Electronique,
de Microélectronique
et de Nanotechnologie
(IEMN), UMR CNRS 8520 , Lille
dans le cadre du
GDR
2501 du CNRS "Etude de la propagation
ultrasonore en milieux non-homogènes en vue du
contrôle non destructif".
|
 |
Une problématique d'Evaluation et de Contrôle Non Destructifs
- de pièces ayant un état de surface irrégulier, - de corrosion, - de qualité de collage de structure, a conduit le Groupement De Recherches (GDR) 2501 du CNRS "Etude de la propagation ultrasonore en milieux non-homogènes en vue du contrôle non destructif" à étudier la propagation dans des guides solides anisotropes [A16], puis fluides, à frontières de formes non régulières (rugosité). Selon les dimensions et les fréquences en jeu, cette dernière étude [A15, A17] peut s'appliquer à d'autres domaines, dont par exemple l'acoustique urbaine (propagation dans des rues en U, tunnels, ...). |
Les matériaux utilisés dans l'industrie n'ont pas toujours un état de surface lisse : il peuvent comporter des "imperfections" et rugosités. La rugosité peut être la conséquence de détériorations à surveiller (corrosion par exemple) ou être recherchée (pour améliorer la qualité d'un collage entre deux matériaux par exemple). A l'heure actuelle, le contrôle industriel se fait principalement en incidence normale (échographie), la structure à contrôler étant inspectée point par point. L'utilisation d'ondes de plaque, appelées ondes de Lamb, qui se propagent dans toute l'épaisseur du matériau parallèlement aux interfaces, permet de contrôler en un seul tir toute une bande de matériau, d'où un gain de temps considérable.
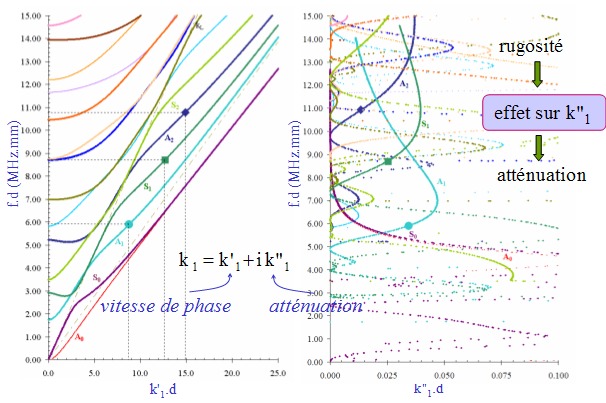
Figure 1 :
Courbes de
dispersion des modes de Lamb dans une plaque de verre fortement
grenaillée. A gauche)
fréquence en fonction de la partie réelle du
nombre d'onde, à droite) fréquence en
fonction de la partie imaginaire du nombre d'onde. Cette partie
imaginaire est
nulle en l'absence de rugosité.
 Figure 2 |
Lorsque les interfaces sont lisses, pour une pulsation donnée
 , six ondes planes se propagent dans une plaque anisotrope, qui se combinent pour donner un mode de Lamb de nombre d'onde k0. , six ondes planes se propagent dans une plaque anisotrope, qui se combinent pour donner un mode de Lamb de nombre d'onde k0.Lorsque
l'interface est rugueuse, les six ondes planes sont diffusées par la
rugosité. A titre d'exemple (figure 2), le mode de Lamb
principal (créé en amont) de nombre d'onde k0 est diffusé par la rugosité, ce qui crée par couplage d'autres modes de Lamb, de nombres d'onde (ka, kb, kc, kd, ...). Ainsi, en raison de la rugosité, l'énergie du mode principal est redistribuée aux autres modes (et
inversement), ce qui se traduit par une perte d'énergie du mode
de Lamb principal k0, et donc par une décroissance de son amplitude.
|
 Figure 3. Observation au point  1 du phénomène de diffusion d'un mode acoustique
sur la rugosité (de hauteur totale notée H( 1 du phénomène de diffusion d'un mode acoustique
sur la rugosité (de hauteur totale notée H(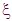 )).
Le premier crochet représente le champ se propageant vers les )).
Le premier crochet représente le champ se propageant vers les 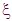 croissants (somme de l'onde primaire
et des ondes couplées "aval") ; le second crochet représente les ondes rétropropagées
de croissants (somme de l'onde primaire
et des ondes couplées "aval") ; le second crochet représente les ondes rétropropagées
de 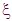 1 à + infini. 1 à + infini.Cliquez sur l'image pour avoir une meilleure définition |
Qualitativement, pour un guide fluide et en l'absence supposée de couplages intermodaux (un seul mode est ici considéré), l'amplitude de pression à l'ordre 1 (notée
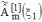 ) fait apparaître l'onde primaire exp(-ik ) fait apparaître l'onde primaire exp(-ik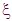 1m 1m 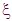 1), celle qui existe en l'absence de rugosité, et les ondes secondaires créées par couplage dû à la diffusion de l'onde primaire sur la rugosité, ce qui provoque une redistribution de l'énergie acoustique sous la même forme modale. 1), celle qui existe en l'absence de rugosité, et les ondes secondaires créées par couplage dû à la diffusion de l'onde primaire sur la rugosité, ce qui provoque une redistribution de l'énergie acoustique sous la même forme modale.
Au point d'observation
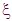 1, arrivent l'onde primaire et des ondes couplées : celles générées en amont de 1, arrivent l'onde primaire et des ondes couplées : celles générées en amont de 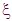 1 et qui se propagent dans le sens de l'onde primaire, et celles générées en aval de 1 et qui se propagent dans le sens de l'onde primaire, et celles générées en aval de 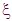 1 qui sont rétropropagées (en rouge sur la figure 3). Les ondes indiquées en vert sur la figure 3 ne contribuent pas au champ de pression au point 1 qui sont rétropropagées (en rouge sur la figure 3). Les ondes indiquées en vert sur la figure 3 ne contribuent pas au champ de pression au point 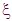 1 . Le détail des calculs se trouve dans la référence [A15]. Voir également les figures 9 à 11. 1 . Le détail des calculs se trouve dans la référence [A15]. Voir également les figures 9 à 11. |
Une étude numérique réalisée à l'IEMN a permis de visualiser le champ formé par l'effet de la rugosité sur l'onde incidente, pour un profil de rugosité périodique. Une première étude analytique qualitative a mis en évidence le couplage de modes par une rugosité traduite sous forme de réaction acoustique de chacun des petits volumes de fluide délimités par le profil de rugosité, et représentée par un opérateur d'impédance ne dépendant pas de la forme de ces petites cavités de fluide [B16, C14, C16].
Une deuxième étude plus quantitative permet de prendre en compte les pentes du profil de rugosité [A15].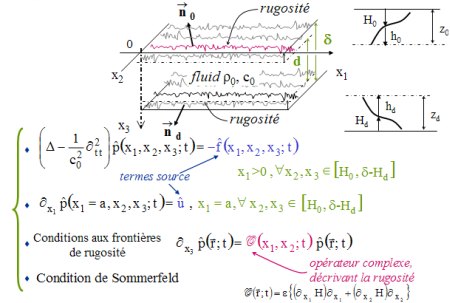 Figure 4 : Géométrie du problème et équations associées Cliquez sur l'image pour avoir une meilleure définition |
Le guide fluide de la figure 4 (masse volumique
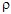 0 et célérité c0)
est limité par des parois parfaitement rigides comportant des frontières
de formes légèrement non régulières en x3=0 (profondeur H0) et en x3=d (profondeur Hd).
La présence de cette rugosité (profondeur totale H=H0+Hd)
conduit à définir deux épaisseurs
caractéristiques, celle du "guide intérieur" d et
celle du "guide extérieur" 0 et célérité c0)
est limité par des parois parfaitement rigides comportant des frontières
de formes légèrement non régulières en x3=0 (profondeur H0) et en x3=d (profondeur Hd).
La présence de cette rugosité (profondeur totale H=H0+Hd)
conduit à définir deux épaisseurs
caractéristiques, celle du "guide intérieur" d et
celle du "guide extérieur" 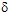 .
Le problème aux valeurs propres considéré dans la
suite est le problème de Neumann associé à ce
guide extérieur. .
Le problème aux valeurs propres considéré dans la
suite est le problème de Neumann associé à ce
guide extérieur. Le problème bien posé s'écrit :
- équation de propagation avec sources de volume, - conditions aux frontières exprimées par une relation entre la dérivée normale de la
pression et la pression elle-même, qui fait intervenir un opérateur complexe
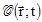 décrivant n'importe quel type de rugosité (opérateur dérivée par rapport à x1 et x2 et fonction de la dérivée du
profil, donc de la pente), décrivant n'importe quel type de rugosité (opérateur dérivée par rapport à x1 et x2 et fonction de la dérivée du
profil, donc de la pente), - condition de Sommerfeld suivant les directions de propagation. Dans
la suite, les variations de profil sont supposées faibles, en terme de hauteur
par rapport à l'épaisseur du guide, et
en terme de pentes.
|
 Figure 5 Cliquez sur l'image pour avoir une meilleure définition |
Décomposition de la pression sur les modes propres transversaux du guide.
La méthode de résolution passe par la "projection" de l'équation de propagation sur les modes propres transversaux du guide. La base modale suivant la coordonnées x3 est prise sur le domaine extérieur à la rugosité (guide d'épaisseur
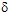 ). ). A noter qu'il existe dans la littérature une méthode "multi-modale" qui repose sur une base différente en chaque point x1 ;
cette base modale est donc locale sur le domaine réel.
La méthode proposée ici, appelée "inter-modale", fait usage d'une base modale unique, sur le guide extérieur d'épaisseur 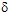 (fonctions propres (fonctions propres 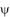 m et nombres d'onde associés km), la "projection" (l'intégration) se faisant sur le domaine réel. m et nombres d'onde associés km), la "projection" (l'intégration) se faisant sur le domaine réel. |
 Figure 6 : Usage du théorème de Green. Cliquez sur l'image pour avoir une meilleure définition |
Formulation modale L'équation de la figure 6
(cas particulier d'une source monochromatique) est obtenue par projection de l'équation
de propagation sur les fonctions propres
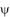 m,
puis par utilisation du théorème de Green 1D qui fait
intervenir les conditions aux frontières (figure 4). Elle fait apparaître les
coefficients modaux du mode m (en vert) mais également ceux des
autres modes µ (créés par couplage), le terme
source (en bleu), et deux termes de couplage (en rouge), l'un relatif
à un opérateur de surface comportant la pente du profil et un opérateur dérivée spatiale, et l'autre à un opérateur de "volume", puisque l'intégration a lieu sur l'épaisseur. m,
puis par utilisation du théorème de Green 1D qui fait
intervenir les conditions aux frontières (figure 4). Elle fait apparaître les
coefficients modaux du mode m (en vert) mais également ceux des
autres modes µ (créés par couplage), le terme
source (en bleu), et deux termes de couplage (en rouge), l'un relatif
à un opérateur de surface comportant la pente du profil et un opérateur dérivée spatiale, et l'autre à un opérateur de "volume", puisque l'intégration a lieu sur l'épaisseur. |
|
Figure 7 : Solution par formulation intégrale (1/2).
Cliquez sur l'image pour avoir une meilleure définition |
Solution par formulation intégrale La solution est cherchée par approximations successives, en faisant usage de la formulation intégrale, et d'un choix de fonction de Green adaptée au problème considéré.
Dans le cas d'une plaque semi infinie, et en supposant que la présence de la source en x1=0
n'empêche pas le champ de se propager dans les deux sens, la
fonction de Green 1D choisie est celle donnée sur la figure 7.
|
|
Figure 8 : Solution par formulation intégrale (2/2).
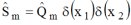 Cliquez sur l'image pour avoir une meilleure définition |
Couplages intermodaux
- A l'ordre 0, la solution n'est autre que le champ incident qui est le seul champ existant lorsque les interfaces sont lisses. - A l'ordre 1, d'autres termes apparaissent, qui représentent les effets de couplage intermodaux dus à la rugosité,
sur toute la longueur de rugosité. Ainsi, les intégrales
de - l'infini à + l'infini montrent bien que la source de
couplage (ici la rugosité) agit comme une source secondaire
étendue. L'expression de la fonction de Green (figure 7) met bien en
évidence le fait que l'effet au point d'observation x1
du couplage en amont et en aval de ce point n'est pas le même. A noter que le système d'équations
(µ,m) n'est pas un système linéaire en raison des
intégrales qui représentent l'effet non local de la
rugosité (d'où la nécessité de faire usage de
la théorie des perturbations).
- Et ainsi de suite jusqu'à l'ordre n. |
|
Figure 9 : Solution directe mono-mode (1/3).
Cliquez sur l'image pour avoir une meilleure définition |
Solution directe mono-mode (hors des sources) Dans le cas particulier d'un seul mode mis en jeu, celui
créé par la source et numéroté m (les
couplages inter-modaux µ étant négligés),
l'équation de la figure 6
prend alors la forme de celle de la figure 9 (le terme source
disparaît puisque supposé hors du domaine d'observation).
Ce cas
particulier n'a d'autre objet que de donner une solution
analytique simple, pour aider à la compréhension des
phénomènes physiques :
le mode m est couplé à lui-même, par
l'intermédiaire des facteurs indiqués en rouge dans
l'équation du bas de la figure 9.
|
|
Figure 10 : Solution directe mono-mode (2/3).
Cliquez sur l'image pour avoir une meilleure définition |
Solution directe mono-mode (suite)
Un développement à l'ordre 1 en fonction de la profondeur de rugosité H=H0+Hd, suivi d'un changement de variable x1 --> 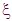 1
(translation à l'ordre le plus bas) permettent d'obtenir
l'équation encadrée de la figure 10, qui est
résolue sous la forme de la somme d'une perturbation 1
(translation à l'ordre le plus bas) permettent d'obtenir
l'équation encadrée de la figure 10, qui est
résolue sous la forme de la somme d'une perturbation 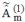 qui s'ajoute à la solution qui s'ajoute à la solution 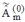 à l'ordre 0 (approximation de Born) : à l'ordre 0 (approximation de Born) :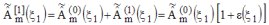 . .Finalement, la perturbation 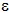 d'ordre 1 est solution de l'équation différentielle (équation de relaxation) d'ordre 1 est solution de l'équation différentielle (équation de relaxation)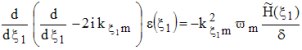 , , |
|
Figure 11 : Solution directe mono-mode (3/3). Phénomènes
de diffusion d'un seul mode sur la rugosité : un
capteur situé au point
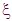 1 recueille
l'onde
primaire, ainsi que les ondes couplées
créées en amont et en aval de ce point
par diffusion sur la rugosité. 1 recueille
l'onde
primaire, ainsi que les ondes couplées
créées en amont et en aval de ce point
par diffusion sur la rugosité. Cliquez sur l'image pour avoir une meilleure définition |
Finalement, l'amplitude de pression
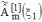 à l'ordre 1 fait apparaître l'onde primaire exp(-ik à l'ordre 1 fait apparaître l'onde primaire exp(-ik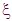 1m 1m 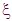 1), celle qui existe en l'absence de rugosité, et les ondes secondaires créées par couplage dû à la diffusion de l'onde primaire sur la rugosité, ce qui provoque une redistribution de l'énergie acoustique sous la même forme modale (puisqu'ici l'approche est monomode). 1), celle qui existe en l'absence de rugosité, et les ondes secondaires créées par couplage dû à la diffusion de l'onde primaire sur la rugosité, ce qui provoque une redistribution de l'énergie acoustique sous la même forme modale (puisqu'ici l'approche est monomode).
Au point d'observation
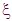 1, arrivent l'onde primaire et des ondes couplées : celles générées en amont de 1, arrivent l'onde primaire et des ondes couplées : celles générées en amont de 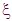 1 et qui se propagent dans le sens de l'onde primaire, et celles générées en aval de 1 et qui se propagent dans le sens de l'onde primaire, et celles générées en aval de 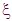 1 qui sont rétropropagées (en rouge sur la figure 3). Les ondes indiquées en vert sur la figure 3 ne contribuent pas au champ de pression au point 1 qui sont rétropropagées (en rouge sur la figure 3). Les ondes indiquées en vert sur la figure 3 ne contribuent pas au champ de pression au point 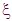 1. Ce petit modèle qualitatif, certes très insuffisant puisqu'il
ne prend pas en compte le couplage intermodal, permet cependant de bien mettre en évidence les
phénomènes physiques de base. Voir également les figures 2 et 3. 1. Ce petit modèle qualitatif, certes très insuffisant puisqu'il
ne prend pas en compte le couplage intermodal, permet cependant de bien mettre en évidence les
phénomènes physiques de base. Voir également les figures 2 et 3. |
|
Figure 12 : Couplages intermodaux dans le cas particulier d'un profil périodique en dents de scie. Les modes créés par couplage dû à la rugosité sont notés µ et le mode généré par la source est noté m.
Cliquez sur l'image pour avoir une meilleure définition |
Couplages intermodaux - Cas particulier d'un profil périodique (période spatiale 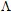 ) en dents de scie ) en dents de scieLe
profil de la figure 12 est périodique : répartition
régulière de N petites cavités (dents) avec une
période spatiale notée
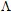 . .Les
sources acoustiques sont supposées ne générer que
le mode m=1, les caractéristiques de rugosité et
la fréquence étant données sur la figure 12 pour
l'air et pour du
verre (solide isotrope dans lequel ne se propagent ici que des ondes
longitudinales). Les modes créés par couplage dû
à la rugosité sont notés µ.
Quatre modes sont pris en compte ici, le mode µ=3 étant évanescent pour la fréquence choisie. L'ordre n=3 suffit généralement pour que le modèle converge. Les résultats sont présentés sur les figures 13 à 17. Les relations de phonon (voir figure 18 et texte y afférent) permettent de prédire un fort ou faible couplage entre les modes, ainsi que les périodes d'oscillation. |
|
Figure 13 : Module
de l'amplitude de pression du mode µ=0 créé par
couplage. La période des oscillations périodiques fait
intervenir la période spatiale
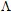 du profil et les nombres d'onde de chaque mode (voir relation de phonon). du profil et les nombres d'onde de chaque mode (voir relation de phonon).Cliquez sur l'image pour avoir une meilleure définition |
Figure 14 : Module
de l'amplitude de pression du mode m=1 créé par la source. Le couplage par rugosité crée d'autres modes que le mode
généré, ce qui provoque la décroissance de son amplitude de pression en fonction de x1.
Cliquez sur l'image pour avoir une meilleure définition |
|
Figure 15 : Module
de l'amplitude de pression du mode µ=2 créé par
couplage. L'amplitude de ce mode est beaucoup moins importante que
celle des modes µ=0 et m=1, comme prédit par la relation
de phonons.
Cliquez sur l'image pour avoir une meilleure définition |
Figure 16 : Module
de l'amplitude de pression du mode µ=3 (évanescent) créé par couplage.
Cliquez sur l'image pour avoir une meilleure définition |
|
Figure 17 : Module de l'amplitude de pression totale.
Cliquez sur l'image pour avoir une meilleure définition |
|
|
Figure 18 : Courbes
de dispersion (lignes épaisses rouge) du guide fluide aux parois
lisses et courbes correspondant à la relation de phonon (lignes
fines bleues).
Cliquez sur l'image pour avoir une meilleure définition |
Relation de phonons Les
périodes d'oscillation des amplitudes de
pression des différents modes (figures 13-17), apparaissent sans
difficulté dans le
cas d'un profil de rugosité sinusoïdal : des termes de
phase et des dénominateurs de la
forme
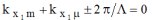 , ,Cette
relation peut être interprétée en termes de
conservation de la quantité de mouvement, en faisant l'analogie
avec les phonons, d'où l'appellation "relation de phonon".
Les
traits épais rouges de la figure 18 sont les courbes de dispersion
classiques des ondes guidées (avec les fréquences de
coupure) pour les quatre premiers modes. Les courbes en traits fins bleus sont les
courbes provenant de la relation de phonon, pour des modes
générés par la source. L'intersection entre les deux courbes permet
de prédire soit un fort auto-couplage du mode m=1 généré par la source avec lui-même (c'est ce qui se produit par exemple à fd/c0=1.26), soit un fort couplage de ce même mode m=1 avec le mode µ=0 créé par couplage (c'est ce qui se produit à fd/c0=1.31).
Et comme ces deux fréquences sont très proches l'une de
l'autre, on comprend bien que dans l'exemple qui précède (figures 12-17),
il y ait à la fois un fort autocouplage du mode
généré par la source m=1 avec lui-même et un
fort couplage de ce mode m=1 avec le mode créé par
couplage
µ=0.
|
|
Figure 19 : Couplages intermodaux dans le cas particulier d'un profil périodique en dents de scie symétrique. Les modes créés par couplage dû à la rugosité sont notés µ et le mode généré par la source est noté m.
Cliquez sur l'image pour avoir une meilleure définition |
Couplages intermodaux - Cas particulier de deux profils périodiques symétriques (période spatiale
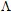 ) en dents de scie ) en dents de scieLe
profil de la figure 19 est périodique : répartition
régulière de N petites cavités (dents) avec une
période spatiale notée
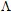 , sur les deux faces du guide (profil symétrique). , sur les deux faces du guide (profil symétrique).Les
sources acoustiques sont supposées ne générer que
le mode m=0
[caractéristiques de rugosité et de fréquence
données sur la figure 19
pour l'air et pour du verre (solide isotrope dans lequel ici ne se
propagent que des ondes longitudinales)]. Les modes créés
par couplage
dû à la rugosité sont notés µ et le
mode généré par la source est noté
m. Les modes tels que (m+µ) impair ont une amplitude nulle (figures 21 et 23).
Quatre modes sont pris en compte ici, le mode µ=3 étant évanescent pour la fréquence choisie. L'ordre n=3 suffit généralement pour que le modèle converge. Les relations de phonon permettent de prédire un fort ou faible couplage entre les modes, ainsi que les périodes d'oscillation. |
|
Figure 20 : Module
de l'amplitude de pression du mode m=0 créé par la source. Le couplage par rugosité crée d'autres modes que le mode
généré, ce qui provoque la décroissance de son amplitude de pression en fonction de x1.
Cliquez sur l'image pour avoir une meilleure définition |
Figure 21 : Module
de l'amplitude de pression du mode µ=1 créé par couplage. L'amplitude
de ce mode est nulle car m+µ=1 (impair).
Cliquez sur l'image pour avoir une meilleure définition |
|
Figure 22 : Module
de l'amplitude de pression du mode µ=2 créé par couplage. L'amplitude
de ce mode est beaucoup moins importante que celle du mode
m=0 comme prédit par la relation de phonons.
Cliquez sur l'image pour avoir une meilleure définition |
Figure 23 : Module
de l'amplitude de pression du mode µ=3 créé par couplage. L'amplitude
de ce mode est nulle car m+µ=3 (impair).
Cliquez sur l'image pour avoir une meilleure définition |
|
Figure 24 : Module de l'amplitude de pression totale.
Cliquez sur l'image pour avoir une meilleure définition |
 En
construction...
En
construction...