Moments multipolaires

Dans tous les cas, les observables collectives que nous calculerons au cours du temps sont les moments multipolaires $D_{lm}(t)$ de la distribution électronique dans une zone d'intégration $B$ :

$$D_{lm}(t)=\int_B\!d{\bf r}\,r^lY_{lm}n({\bf r},t)$$

où $n({\bf r},t)$ est la densité électronique à l'instant $t$ et $Y_{lm}$ une harmonique sphérique. Par exemple, les moments dipolaires ($l=1$) sont reliés à la section efficace de photoabsorption de l'agrégat et traditionnellement utilisés dans les études linéarisées, car reliés directement à la réponse du nuage électronique à une excitation lumineuse : la résonance plasmon en particulier se manifeste par une oscillation du moment dipolaire.

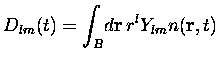
La zone d'intégration $B$ doit être limitée au voisinage de l'agrégat, car au cours d'une excitation violente une émission directe d'électrons de l'agrégat prend place, comme nous allons le montrer plus bas, et ce courant brouillerait $D_{lm}(t)$ si cette précaution n'était pas prise. En pratique, nous prenons pour $B$ une sphère de rayon $R+2r_s$ dans le cas sans symétrie ou un cylindre de la même étendue dans les études à symétrie axiale ($r_s$ étant le rayon de Wigner-Seitz du métal).

Nous désignerons pour le moment par $D(t)$ le moment dipolaire du nuage électronique($l=1$, $m=0$) suivant un axe $z$ arbitraire (ce sera en particulier l'axe de symétrie lorsque la dynamique sera contrainte à garder la symétrie axiale). Le signal $D(t)$ subit une transformée de Fourier dans le domaine des fréquences pour donner plus de précisions sur les propriétés spectrales du signal :

$$\widetilde{D}(\omega)=\int dt e^{i\omega t}D(t)$$

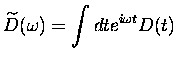
Négligeant pour le moment le manque de précision dû à l'intervalle de temps fini et discret sur lequel est disponible $D(t)$, la question se pose alors de savoir quelle quantité d'information peut être extraite de $\widetilde{D}(\omega)$.