Modélisation de l'impulsion laser

Les effets de l'impulsion laser femtoseconde sur la dynamique du nuage électronique sont pris en compte par un potentiel $V_{\mbox{{\scriptsize laser}}}$ qui est rajouté au potentiel extérieur dans les équations de Kohn-Sham dépendant du temps. Négligeant le champ magnétique créé par le laser, et avec un choix de jauge adéquat [48] ce potentiel en un point de rayon vecteur ${\bf r}$ vaut

$$V_{\mbox{{\scriptsize laser}}}({\bf r})={\bf r}.{\bf E}$$

où ${\bf E}$ est le champ électrique créé par le laser. Ici, pour pouvoir traiter le cas d'un laser avec une polarisation arbitraire nous prenons

$${\bf E}=f(t)E_0({\bf e}_1\cos (\omega t)+{\bf e}_2\cos (\omega t+\phi))$$

avec ${\bf e}_1$ et ${\bf e}_2$ deux vecteurs orthonormés décrivant le plan de vibration du champ électrique, $\omega$ la pulsation du laser, $E_0$ l'intensité du champ électrique, $f(t)$ un facteur de modulation temporelle de l'intensité pour pouvoir décrire l'enveloppe de l'impulsion femtoseconde. Nous avons choisi une forme gaussienne

$$f(t)=e^{\displaystyle -\left(\frac{t-t_{\mbox{{\scriptsize max}}}}{\Delta t}\right)^2}$$

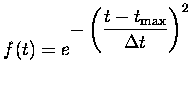
avec des paramètres $t_{\mbox{{\scriptsize max}}}$ et $\Delta t$ choisis pour que le champ laser soit petit à $t=0$, et pour avoir une largeur temporelle de 35 fs.

Le champ $E_0$ a une valeur de 0,0235 dans nos unités, ce qui correspond (voir l'annexe D) à une puissance de 4,9$.10^{12}$ $W/cm^2$.

Comme il l'a été démontré dans [29] et les articles ultérieurs, une telle impulsion femtoseconde ionise l'agrégat. La résolution des équations de Kohn-Sham fait cependant appel à des algorithmes explicitement unitaires, et pour tenir compte de cette ionisation nous avons introduit les conditions aux limites absorbantes décrites page  dans la simulation temporelle.