Le rôle des conditions aux limites absorbantes est d'éliminer des calculs les fonctions d'onde qui sont dans le continuum. Comme les équations utilisées dans la modélisation sont des équations de champ moyen, la norme de chaque fonction d'onde sera affectée par les conditions absorbantes, et on n'aura jamais exactement un nombre entier de fonctions d'onde éliminées. Comme il l'a été démontré dans [48], à propos d'atomes d'hélium soumis à des impulsions laser femtoseconde, cette méthode donne cependant de très bonnes indications sur les processus physiques impliqués, en particulier sur le nombre total de particules émises en fonction de l'énergie d'excitation stockée dans le système.
Il faut choisir des conditions aux limites absorbantes qui n'influencent pas la dynamique par d'autres effets que l'atténuation des fonctions d'onde ; en particulier, si on impose comme condition une simple annulation aux bords de la boîte, cela est tout à fait similaire aux conditions aux limites de la propagation des fonctions d'onde effectuée par la méthode de Crank-Nicholson qui suppose une fonction d'onde nulle à l'extérieur, et introduit donc une réflexion parasite de la partie non atténuée des fonctions d'onde sur le bord de la boîte.
Nous avons par conséquent choisi de multiplier les fonctions d'onde en
chaque point de la boîte distant de moins de ![]() d'une paroi par le facteur
d'une paroi par le facteur
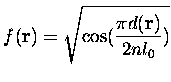
où
![]() représente la distance du point
représente la distance du point ![]() à chaque paroi
de la boîte,
à chaque paroi
de la boîte, ![]() est une longueur caractéristique, que nous fixons
égale au pas de réseau, et
est une longueur caractéristique, que nous fixons
égale au pas de réseau, et ![]() le nombre de points de réseau sur lequel
se fait l'atténuation, que nous avons pris égal à 3.
le nombre de points de réseau sur lequel
se fait l'atténuation, que nous avons pris égal à 3.
Dans ces conditions, avec une boîte suffisamment grande, l'absorption se fait de façon progressive, pratiquement sans réflexions parasites. On peut cependant objecter que la disparition non-physique de charges du calcul doit modifier quelque peu le résultat par rapport au résultat exact.
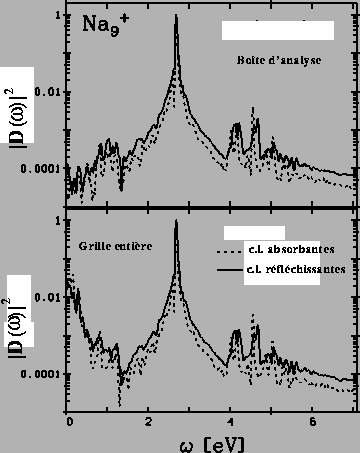
Nous illustrons sur la figure I.4 les différences induites sur les spectres par le choix des différentes conditions aux limites, réfléchissantes ou absorbantes. La concordance évidente des résultats montre que l'emploi de différentes conditions aux limites n'a que peu d'influence sur les spectres.
|
Cette figure illustre de plus l'effet de l'emploi de la boîte d'analyse dans le calcul dynamique. Cette boîte élimine du calcul des observables les oscillations dans la boîte du nuage d'électrons émis. Sur la partie inférieure de la figure, cette boîte n'est pas utilisée ; il en résulte l'apparition d'un pic à basse énergie, à la fréquence correspondant à l'oscillation du nuage des électrons émis. Cette fréquence décroît avec la taille de la boîte employée dans le calcul. Pour les conditions aux limites absorbantes, on a par contre un pic à énergie nulle correspondant au flux d'électrons quittant l'agrégat.