|

|
|
|
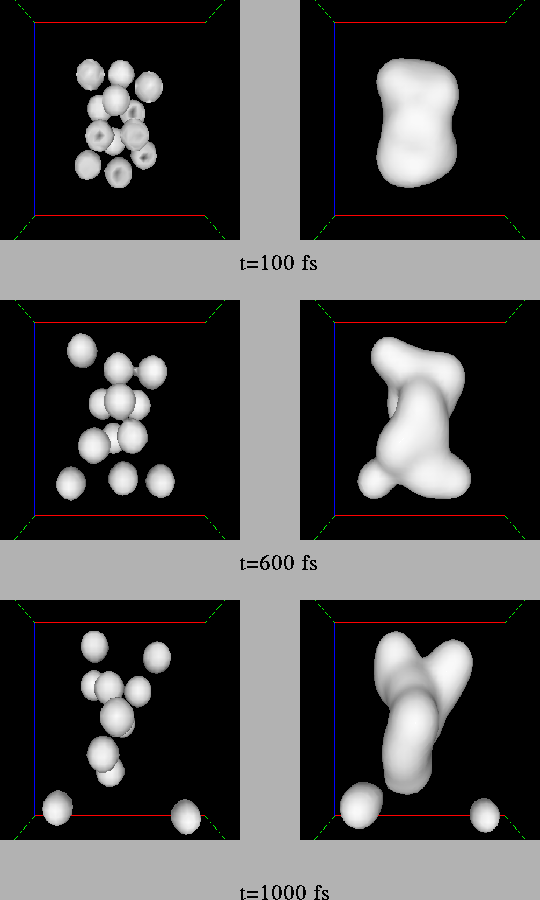
Dans la suite du calcul, les oscillations du nuage électronique s'amortissent rapidement, puisque la fréquence choisie pour le laser est très différente de la fréquence plasmon, et les ions commencent à bouger puisque leur géométrie d'équilibre a changé. En fait, cette adaptation est ici impossible, et l'évolution de la structure ionique avec dynamique électronique liée commence par l'émission de deux ions, accompagnée de l'émission d'un électron et demi.
|
Il reste alors dans la zone de calcul un agrégat
Na![]() approximativement, lui aussi instable ; il expulse alors successivement
plusieurs fragments, ce qui ne suffit toujours pas à le stabiliser.
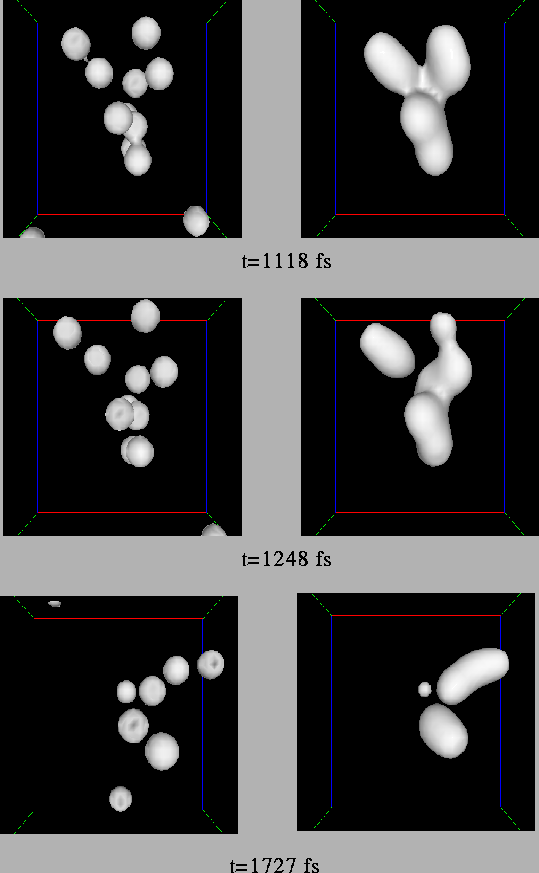
Finalement, on assiste à la destruction complète de l'agrégat sur
une échelle de temps de 2 ps.
approximativement, lui aussi instable ; il expulse alors successivement
plusieurs fragments, ce qui ne suffit toujours pas à le stabiliser.
Finalement, on assiste à la destruction complète de l'agrégat sur
une échelle de temps de 2 ps.
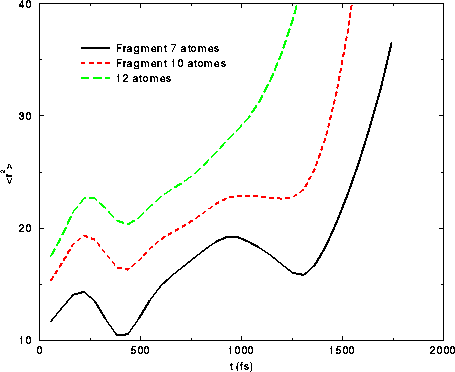
L'expulsion de fragments par un phénomène qu'on pourrait qualifier de <<fission>> est manifeste sur la figure III.15, qui représente le rayon carré moyen au cours du temps de groupes d'atomes constituant l'agrégat. Les bosses de ces courbes correspondent à une réorganisation importante de la structure ionique ; on vérifie bien que deux atomes sont d'abord expulsés, suivis de trois. Nous avons pu identifier les atomes de chaque fragment d'une part grâce aux isosurfaces électroniques tracées sur les figures III.12, qui nous ont donné un seuil de densité pour lequel ces isosurfaces se séparent en plusieurs fragments, d'autre part grâce à un programme développé initialement pour la physique nucléaire par E.Suraud, qui, grâce à une technique de percolation autour des fragments définis par le seuil trouvé précédemment, peut donner automatiquement la taille et la position de ces fragments électroniques avec une assez bonne précision.
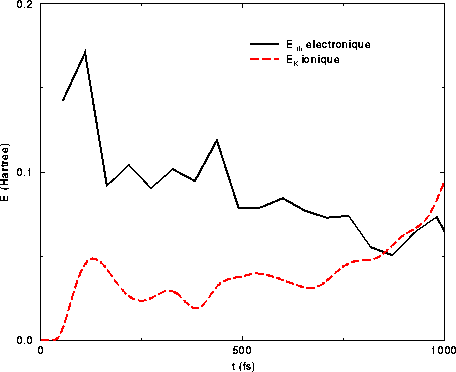
On peut analyser ce phénomène d'explosion par le transfert d'énergie du nuage électronique, fortement chauffé par l'impulsion laser, aux degrés de liberté ioniques. Nous traçons sur la figure III.14 cette énergie thermique électronique, définie par E.Suraud et P.G.Reinhard par
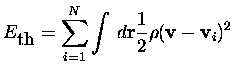
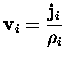
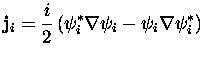
Moyennant les différences éventuelles d'énergie cinétique de point zéro des fonctions d'onde, cette quantité mesure en quelque sorte l'agitation locale des particules, en éliminant un mouvement d'ensemble de translation (il n'y a pas de rotation locale). On peut donc bien parler d'énergie thermique. Sur la figure III.14, on peut vérifier que cette énergie, initialement élevée par suite du chauffage par l'impulsion laser femtoseconde, décroît quasiment constamment par transfert d'énergie aux degrés de liberté ioniques. L'énergie cinétique ionique est représenté sur la même figure, dans le domaine où elle a un sens (voir plus loin pour cette discussion). On vérifie en effet que l'échelle de temps du transfert d'énergie des degrés de liberté électroniques vers les degrés de liberté ioniques est petite, et vaut moins de 200 fs. Durant la première centaine de femtosecondes en tout cas, les ions sont quasiment immobiles, ce qui justifie a posteriori notre choix d'uner structure ionique gelée dans tous les calculs de dynamique électronique que nous avons effectués auparavant, y compris dans les régimes fortement non-linéaires.