L'émission de fragments ne se fait donc pas sous la forme d'un agrégat
Na
quittant l'agrégat, ce qu'on pourrait attendre d'après les résultats
expérimentaux ou ceux de calculs contraints avec l'approximation Born-Oppenheimer
de [65], qui arguent que dans une telle fission le chemin
qui mène à deux fragments possédant un nombre magique d'électrons de
valence est le plus favorisé. On ne voit pas en effet pourquoi ce chemin,
qui est certes sans doute celui présentant la barrière la plus basse,
serait suivi lors d'une évolution en dynamique adiabatique ou
non-adiabatique du système. Il faudrait sans doute moyenner sur un grand
nombre de simulations avec des conditions initiales différentes pour
trouver que ce chemin est, dans l'ensemble, le plus favorisé.
Vu le temps que nécessite une seule simulation, cette moyenne d'ensemble
est impossible pour le moment à réaliser.
|
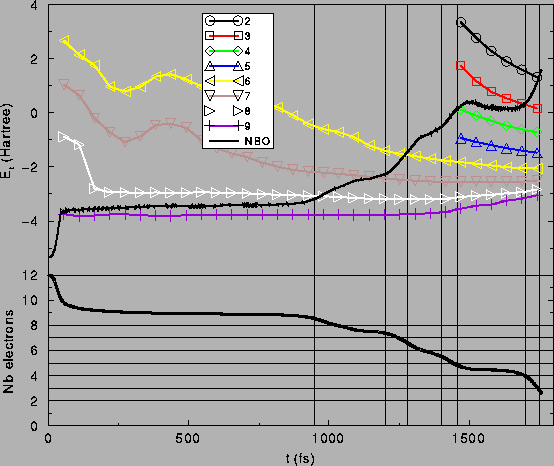
Une autre question qui peut se poser est celle de la pertinence d'une étude non-adiabatique dans ce cas. Il faut donc comparer, comme nous l'avions fait plus haut, les résultats à ceux d'une simulation Born-Oppenheimer. Le problème ici est que nous avons inclus des conditions aux limites absorbantes ; les électrons qui sont éventuellement émis après l'excitation initiale vont être absorbés par ces conditions aux limites. Il est impossible d'introduire de telles conditions aux limites dans un calcul Born-Oppenheimer, qui nécessite le calcul de l'état fondamental électronique de l'agrégat à chaque pas de temps ionique. Nous avons néanmoins simulé cet effet en comparant à certains pas de temps l'état fondamental Born-Oppenheimer du système pris avec la configuration ionique donnée par le calcul non-adiabatique, pour différents nombres d'électrons de valence variant entre 9 et 2. Ces résultats sont présentés sur la figure III.16, où l'énergie totale et le nombre d'électrons total au cours de la simulation non-adiabatique sont également tracés. On voit qu'à différents instants, l'énergie obtenue dans le calcul non-adiabatique est toujours supérieure à l'énergie du fondamental avec un nombre d'électrons de valence entier très proche du nombre d'électrons présents dans la simulation non-adibatique, pour la même configuration ionique.
Notons que nous avons forcé dans le
cas où le nombre d'électrons de valence n'est pas pair l'occupation
de deux orbitales par l'électron d'énergie la plus élevée, avec un
facteur d'occupation fractionnaire égal à 
. Cette modification est
à notre avis nécessaire, car l'impulsion laser ne comporte pas de terme
magnétique et ne peut donc pas polariser en spin au cours du temps le
nuage électronique ; comme celui-ci n'est pas polarisé au départ, il ne
le sera jamais au cours du temps dans le calcul non-adiabatique.
Cette précaution conduit à prendre en compte des états légèrement
excités dans le calcul adiabatique, ce qui doit très peu changer les
résultats.
On voit en tout cas sur la figure III.16 que le système évolue au départ de façon assez proche du résultat adiabatique avec 9 électrons ; cependant, il s'en éloigne à partir du moment ou le premier fragment explusé, avec son nuage électronique qui l'accompagne, franchit les bords de la boîte et donc que ce nuage est absorbé, et de même pour la dynamique ultérieure avec un nombre d'électrons total plus faible. Ceci justifie au moins l'intérêt d'une telle simulation non-adiabatique dans le cas où des fragments éventuellement neutres sont émis ; en travaillant comme nous le faisons sur réseau, il faudrait prendre une boîte véritablement énorme pour traiter correctement cette émission de fragments non entièrement ioniques. Notons justement à ce propos que les auteurs de [52], qui calculaient eux aussi sur réseau avec une dynamique adiabatique, s'étaient limités à cette émission d'ions.
Cette émission de fragments non entièrement ioniques pose en tout cas un problème de principe, puisque comme les électrons qui les accompagnent sont absorbés en sortant de la boîte, les fragments émis se transforment en fragments purement ioniques et peuvent donc perturber la dynamique à l'intérieur de la boîte de façon différente du cas où ils auraient une charge moins forte. Nous ne pensons pas que ce problème se pose dans la simulation dont nous présentons ici les résultats ; en effet, l'agrégat qui reste au centre de la boîte est fortement chargé, et les ions correspondants exercent donc sur les électrons de valence un effet nettement plus fort qu'un éventuel ion à la périphérie ; de plus, il n'y a jamais eu de charge entière compensant exactement une charge ionique émise (donc pas d'émission de monomères ou autres isomères neutres), ce qui fait que la perturbation, qui s'exerce de toute façon à grande distance puisque la boîte est relativement grande, doit être assez petite.
On pourrait contourner cette difficulté en utilisant des pseudodensités ioniques sur le réseau plutôt que des pseudopotentiels analytiques ; ces densités s'annuleraient dans le cas d'émission de monomères neutres par exemple, et l'effet dont nous discutions au paragraphe précédent serait compensé. Dans ce cas évidemment, le problème inverse se pose : lors de l'émission d'ions, l'effet de l'ion cesse dès qu'il quitte la boîte. La réalité (du moins celle de la LDA adiabatique, qui ne quantifie pas correctement le nombre d'électrons émis) se trouve probablement à mi-chemin entre ces deux méthodes extrêmes ; il semble cependant assez difficile de définir une méthodologie correcte pour traiter ce problème dans le cadre que nous avons choisi.
Ce problème en tous cas rend faux le calcul de l'énergie cinétique emportée par les différents fragments, car c'est par son comportement asymptotique qu'on peut la calculer, et ici ce comportement asymptotique est biaisé par cet effet d'annulation des charges émises. Cet inconvénient est relativement grave, car les expériences sur la question peuvent mesurer le contenu énergétique des fragments émis.
Le calcul dont nous présentons ici les résultats est en tout cas à notre connaissance la première simulation directe de l'explosion d'un agrégat induite par une impulsion laser femtoseconde. De plus, l'intérêt d'une simulation non-adiabatique est manifeste.
Nous avons d'autre part effectué la même simulation en réglant la fréquence
de l'impulsion laser à une valeur proche de la fréquence plasmon de
l'agrégat, et en choississant la valeur du champ électrique de façon à
ce que deux électrons exactement soient émis lors du processus
d'excitation. Dans ce cas, nous avons observé un chauffage de
l'agrégat, et une subsistance des oscillations du nuage électronique
après la fin de l'impulsion laser (puisque le plasmon a été excité),
mais aucune fragmentation n'avait eu encore lieu après 2 ps
de simulation, lorsque nous avons arrêté le calcul. Dans ce dernier cas
donc, il s'agit plus d'une émission statistique (du point de vue
thermodynamique
Na
est instable)
qu'une émission directe comme celle qui avait lieu
dans l'exemple que nous venons de
discuter en détail.
au cours du calcul en dynamique non-adiabatique avec l'énergie de l'état
fondamental électronique avec les mêmes configurations ioniques, à
différents instants. Le nombre total d'électrons présents dans la boîte
de calcul est également tracé sur le graphe inférieur, avec des droites
indiquant les points d'intersection des courbes dans le graphe
supérieur.