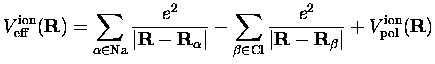 |
(50) |
Pour la partie agissant sur les ions, nous prenons
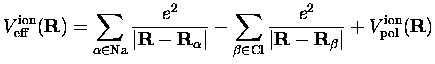 |
(50) |
Le terme de polarisation est construit de façon analogue à la partie
ionique mais avec un terme de coupure rendu nécessaire par le fait que les
électrons peuvent se trouver à une distance arbitrairement proche de la
surface. Sa forme est inspirée par le potentiel utilisé
dans [63], où tout le poids de l'interaction effective était subi
par les électrons. Ici, les paramètres en sont donc quelque peu
différents. La coupure dans
![]() est ajustée sur le gap
de NaCl(100), qui vaut
est ajustée sur le gap
de NaCl(100), qui vaut
![]() au point
au point ![]() de la zone de
Brillouin, et débute à
de la zone de
Brillouin, et débute à
![]() de la surface du substrat.
de la surface du substrat.
Le minimum des deux termes de polarisation est placé à ![]() .
La surface (du moins en moyenne) est donc à
.
La surface (du moins en moyenne) est donc à ![]() , avec
, avec
![]() . Le potentiel
. Le potentiel
![]() décrit l'effet
de la corrugation. Les paramètres
décrit l'effet
de la corrugation. Les paramètres ![]() et
et ![]() de la
corrugation sont les mêmes que dans [63].
Les autres paramètres,
de la
corrugation sont les mêmes que dans [63].
Les autres paramètres,
![]() et
et ![]() sont ajustées aux résultats ab initio : l'énergie de liaison d'un
monomère neutre de sodium au dessus d'un ion chlore est
sont ajustées aux résultats ab initio : l'énergie de liaison d'un
monomère neutre de sodium au dessus d'un ion chlore est
![]() , au dessus d'un ion sodium
, au dessus d'un ion sodium
![]() , au dessus d'un vide
, au dessus d'un vide
![]() ,
et la différence d'énergie de liaison au substrat entre la configuration
planaire de
Na
,
et la différence d'énergie de liaison au substrat entre la configuration
planaire de
Na![]() et celle qui est tridimensionnelle vaut
et celle qui est tridimensionnelle vaut
![]() .
.
Ces résultats sont reproduits par les paramètres
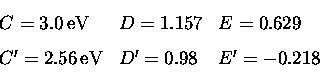 |
(58) |