Paramètres des pseudopotentiels

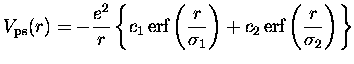
Dans cet annexe, nous allons donner les paramètres des pseudopotentiels locaux que nous avons utilisés : ceux-ci ont été choisis à la fois pour donner des résultats physiques sensés et pour être représentés de façon optimale sur la grille d'espace tridimensionnelle que nous avons utilisée pour représenter les variables spatiales.

Rappelons que dans le cas des agrégats de sodium nous utilisons des pseudopotentiels locaux, à symétrie sphérique, construits à partir de deux fonctions d'erreur :

$$V_{\mbox{\scriptsize ps}}(r) = -\frac{e^2}{r} \left\{ c_1\, \mbox... ...{r}{\sigma_1}\right) +c_2\, \mbox{erf}\left(\frac{r}{\sigma_2}\right) \right\}$$

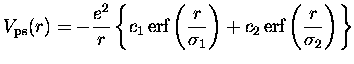
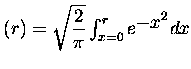où erf désigne la fonction d'erreur normalisée ( $$$$   erf$(r)=\sqrt{\displaystyle\frac{2}{\pi}} \int_{x=0}^{r} e^{\displaystyle -x^2}dx$) qui tend vers 1 pour $r\to\infty$, ce qui donne un comportement asymptotique sensé pour le pseudopotentiel, à condition que

$$c_1\,+c_2\,=1$$ (46)

(nous prenons un électron de valence par atome de sodium).

La pseudodensité ionique $\rho_{\mbox{\scriptsize ps}}$ est définie par

$$\Delta V_{\mbox{\scriptsize ps}}+4\pi e^2 \rho_{\mbox{\scriptsize ps}}=0$$

Comme

$$\Delta V(r) = \frac{1}{r}\partial_r^2 (rV)$$

on a

$$\rho_{\mbox{\scriptsize ps}}(r)=c_1\, {\cal G}_{\sigma_1}(r) +c_2\, {\cal G}_{\sigma_2}(r)$$ (47)

où ${\cal G}_{\sigma}$ désigne une gaussienne normalisée

$${\cal G}_{\sigma}(r) = (\pi\sigma^2)^{-3/2}e^{\displaystyle -\frac{r^2}{\sigma^2} }$$

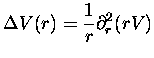
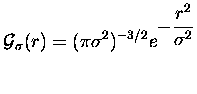
Pour caractériser ces pseudopotentiels, nous utilisons leur << force >> $S_{\mbox{\scriptsize ps}}$ définie par la mesure de la différence du pseudopotentiel avec un potentiel coulombien :

$$S_{\mbox{\scriptsize ps}}=\int\!d{\bf r}\,(V_{\mbox{\scriptsize ps}}(r)+\frac{e^2}{r})$$

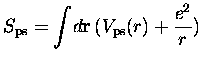
ce qui s'exprime en fonction de la pseudodensité par

$$S_{\mbox{\scriptsize ps}} = \frac{2\pi e^2}{3}\int\!d{\bf r} \,r^2\,\rho_{\rm ps}(r) \quad.$$

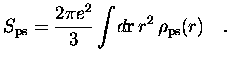
c'est à dire qu'il y a proportionnalité avec le rayon carré moyen de cette pseudodensité.

Pour la pseudodensité définie par E.2 cette relation donne

$$S_{\mbox{\scriptsize ps}} = \pi e^2\left[c_1\sigma_1^2+c_2\sigma_2^2\right]$$ (48)

Le problème de la représentation sur réseau se pose alors. L'expérience de travaux antérieurs de Reinhard et Suraud a montré que des gaussiennes de largeur ${\cal G}_{\sigma}$ étaient représentées de façon optimale sur un réseau tridimensionnel à maille la plus lâche possible à condition que l'espacement $\Delta r$ des points de ce réseau soit égal à la largeur à mi-hauteur de ${\cal G}_{\sigma}$, soit

$$\sigma= \frac{1}{\sqrt{\mbox{ln}2}} \Delta r$$ (49)

Dans ces conditions, la normalisation des gaussiennes est très bien vérifiée par intégration numérique.

Il faut noter qu'il existe quatre coefficients pour nos pseudopotentiels (deux largeurs et deux poids). Ils sont reliés par les relations E.1, E.3, et E.4. Si on impose deux relations de type E.4, comme nous l'avons fait pour imiter les pseudopotentiels légèrement différents utilisés dans [38], tous les coefficients sont définis, bien que le choix du pas de réseau soit assez arbitraire (nous avons pris dans ce cas $\Delta r=0.8$a$_0$, ce qui était le choix de [38], ce qui a fixé $\sigma_1$, et pris $\sigma_2=2\sigma_1$ afin que la deuxième gaussienne soit représentée parfaitement sur le réseau). Dans un deuxième temps, vu que les résultats pour la position du pic plasmon obtenus avec ces pseudopotentiels n'étaient pas satisfaisants, nous avons pris un pas de réseau un peu plus serré et une force plus grande pour les pseudopotentiels.

Les paramètres employés peuvent ainsi être résumés dans le tableau suivant :

	CAPS	plasmon mieux placé
$\Delta r$	0,8	0,6366
$\sigma_1$	0,96089	0,76472
$\sigma_2$	1,92179	1,41421
$c_1$	-0,90216	-4,20716
$c_2$	1,90216	5,20716
$S_{\mbox{\scriptsize ps}}$	38,907	49,97