


Next: Théorie de la fonctionnelle
Up: these
Previous: Organisation
Table des matières
Cadre théorique
Dans ce chapitre, nous allons présenter les bases théoriques de notre
travail.
Rappelons que nous cherchons à modéliser la dynamique des électrons de valence
d'un agrégat après une excitation violente par une impulsion laser
femtoseconde intense ou par un ion multichargé passant à proximité.
Puisque dans ces cas une forte quantité d'énergie est déposée dans
l'agrégat, les linéarisations sont impossibles et
l'approche la plus efficace est de simuler directement en
temps la réponse des électrons de valence. Il faut donc choisir une
modélisation de l'agrégat qui tienne compte explicitement de ces électrons,
et qui puisse servir à calculer aussi bien l'état
fondamental de l'agrégat (avant excitation) qu'une réponse dépendant du
temps, c'est à dire l'ensemble des valeurs de certaines observables sur
un intervalle de temps incluant une perturbation.
Nous séparerons les systèmes que nous étudions en deux parties :
- l'ensemble des noyaux atomiques et électrons de c
 ur, fortement liés
au noyau, que nous ne traiterons pas explicitement pour cette raison.
Nous assimilerons plutôt en un seul objet chaque noyau et ses électrons
de c
ur, fortement liés
au noyau, que nous ne traiterons pas explicitement pour cette raison.
Nous assimilerons plutôt en un seul objet chaque noyau et ses électrons
de c ur, que nous appellerons dans la suite << ion >> . Les effets
éventuels des électrons de c
ur, que nous appellerons dans la suite << ion >> . Les effets
éventuels des électrons de c ur seront pris en compte par des
pseudopotentiels. Ces objets seront fixes ou lentement mobiles.
ur seront pris en compte par des
pseudopotentiels. Ces objets seront fixes ou lentement mobiles.
- les électrons restants, que nous appellerons électrons de valence.
Dans la majorité de nos études sur le sodium, il y aura ainsi un
électron de valence par atome de sodium. Pour les éléments de ce
sous-système, qui sont légers et rapidement mobiles, il faudra résoudre
explicitement les équations du mouvement sur l'intervalle de temps
considéré.
Précisons les échelles de temps et de distance en jeu. L'exemple-type du système
que nous allons étudier est un agrégat
de sodium d'une dizaine d'atomes soumis à une impulsion laser
femtoseconde. L'échelle de temps est la femtoseconde pour le mouvement
des électrons, quelques centaines de femtosecondes pour le mouvement des
ions, l'échelle de distance est le bohr(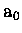 ), l'échelle d'énergie
l'électron-volt.
), l'échelle d'énergie
l'électron-volt.
![[*]](foot_motif.gif) Dans ces conditions, les électrons de valence doivent
être traités quantiquement, mais nous pourrons supposer que le mouvement
ionique est essentiellement classique.
Dans ces conditions, les électrons de valence doivent
être traités quantiquement, mais nous pourrons supposer que le mouvement
ionique est essentiellement classique.
Le Hamiltonien total du système peut alors s'écrire de façon
schématique (nous reprendrons en détail les différents termes à la fin
de ce chapitre) :
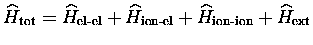 |
(1) |
Les interactions que nous avons à définir sont donc les suivantes :
-
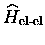 l'interaction entre
électrons de valence. Nous
utilisons pour cette question la théorie de la fonctionnelle de la
densité, que nous allons présenter dans le cas statique, pour calculer
l'état fondamental électronique, comme dans le cas dépendant du temps
où certaines précautions seront à prendre.
l'interaction entre
électrons de valence. Nous
utilisons pour cette question la théorie de la fonctionnelle de la
densité, que nous allons présenter dans le cas statique, pour calculer
l'état fondamental électronique, comme dans le cas dépendant du temps
où certaines précautions seront à prendre.
-
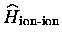 l'interaction
entre ions : lorsqu'il faut en tenir compte, nous utilisons
essentiellement un terme classique d'interaction entre charges.
l'interaction
entre ions : lorsqu'il faut en tenir compte, nous utilisons
essentiellement un terme classique d'interaction entre charges.
-
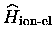 l'interaction ions-électrons de valence : dans un premier temps,
nous ne tiendrons compte de celle-ci que d'une façon moyenne grâce au
modèle du << jellium >>, tout à fait pertinent pour le sodium, métal
auquel nous avons essentiellement consacré nos efforts. Ensuite, nous
présenterons les pseudopotentiels d'abord locaux, puis non-locaux, que
nous avons utilisés.
l'interaction ions-électrons de valence : dans un premier temps,
nous ne tiendrons compte de celle-ci que d'une façon moyenne grâce au
modèle du << jellium >>, tout à fait pertinent pour le sodium, métal
auquel nous avons essentiellement consacré nos efforts. Ensuite, nous
présenterons les pseudopotentiels d'abord locaux, puis non-locaux, que
nous avons utilisés.
- enfin, puisque les agrégats que nous étudions sont libres mais
sujets à des
perturbations extérieures, nous allons indiquerons comment nous avons pu faire
intervenir dans notre modèle l'effet de différentes perturbations
extérieures
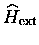 . Ceci nous amènera à
discuter de la pertinence de différentes observables quantiques.
. Ceci nous amènera à
discuter de la pertinence de différentes observables quantiques.
Nous serons alors en mesure d'exprimer l'énergie totale du système, et nous
en déduirons les équations du mouvement des ions.



Next: Théorie de la fonctionnelle
Up: these
Previous: Organisation
Table des matières
Florent Calvayrac
1999-05-05
![]() ), l'échelle d'énergie
l'électron-volt.
), l'échelle d'énergie
l'électron-volt.
![[*]](foot_motif.gif) Dans ces conditions, les électrons de valence doivent
être traités quantiquement, mais nous pourrons supposer que le mouvement
ionique est essentiellement classique.
Dans ces conditions, les électrons de valence doivent
être traités quantiquement, mais nous pourrons supposer que le mouvement
ionique est essentiellement classique.