Équation de conjugaison de Descartes, grandissements
Les points principaux \(H\) et \(H'\) sont pris comme origine :
\(\overline{HA} = z\)
et
\(\overline{H'A'} = z'\)
d'où
\(\overline{FA} = z-f\)
et
\(\overline{F'A'} = z' -f'\)
En remplaçant dans (21), l'équation de conjugaison devient :
\(\frac{n'}{z'} = \frac{n}{z} + \frac{n'}{f'} = \frac{n}{z} + Cv \mbox{ (23)}\)
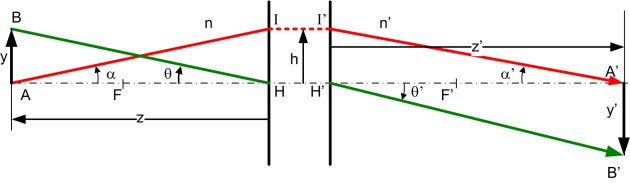
Suivant la figure 38, le rayon (vert) issu de \(B\) et passant par \(H\) fait un angle \(\theta\) avec l'axe. Comme montré précédemment, son image partant de \(H'\) fait un angle \(\theta '\) tel que \(n \theta = n' \theta '\). Comme \(\theta = y/z\) et \(\theta ' = y'/z'\), on en déduit le grandissement transversal \(g_{y}\) :
\(g_{y} = \frac{\overline{A'B'}}{\overline{AB}} = \frac{y'}{y} = \frac{nz'}{n'z} \mbox{ (24)}\)
avec (22) et (23) :
\(g_{y} = \frac{f}{f-z} = 1- \frac{z'}{f'} \mbox{ (25)}\)
A une seule valeur de \(z\) (ou de\( z'\)) correspond une seule valeur de \(g_{y}\) et réciproquement. Ces formules sont identiques à celles des dioptres. Pour un dioptre, les plans principaux sont confondus et situés sur la surface du dioptre.
Le même type raisonnement conduit au grandissement angulaire \(g_{\alpha}\) :
\(g_{\alpha} = \frac{\alpha '}{\alpha} = \frac{z}{z'} \mbox{ (26)}\)
et au grandissement axial \(g_{z}\) :
\(g_{z} = \frac{dz'}{dz} = \frac{n}{n'} \cdot \frac{z'^{2}}{z^{2}} \mbox{ (27)}\)