Coordonnées homogènes dans l'espace
Définition : Coordonnées homogènes dans l'espace
Un point X dans l'espace
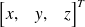(coordonnées inhomogènes) est représenté par 4 coordonnées homogènes
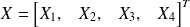avec
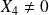
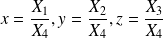
Définition : Plan dans l'espace
Un plan dans l'espace peut s'écrire sous la forme :
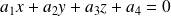
Les coordonnées homogènes d'un plan sont
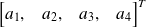
En remplaçant
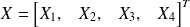dans l'équation du plan ey en multipliant par X_4 on obtient
a_1 X_1 + a_2 X_2+ a_3 X_3+ a_4 X_4=0 qui peut s'écrire plus simplement
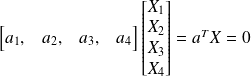
Complément : Plan défini par trois points
Soit trois points
,
,
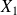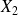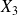définissant un plan X un point quelconque de l'espace. L'équation du plan défini par ces trois points est égal au déterminant de la matrice M avec
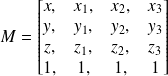
Complément : Trois plans définissent un point
Un point X appartient à un plan a si
. Lorsqu'on a 3 plans l'équation précédente est répétée 3 fois. On obtient un système de 3 équations à 3 inconnues. Si les 3 plans sont distincts alors ce système possède une solution unique : un point.
Définition : Matrice de rotation
Une rotation autour de l'axe z s'écrit sous la forme d'un angle
:
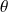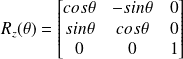
Une rotation autour de l'axe y s'écrit sous la forme d'un angle
:
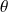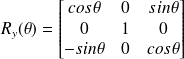
Une rotation autour de l'axe x s'écrit sous la forme d'un angle
:
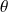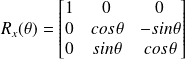
Définition : Matrice de rotation en coordonnées homogènes
Une rotation autour de l'axe z s'écrit sous la forme d'un angle
:
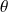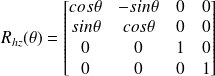
Une rotation autour de l'axe y s'écrit sous la forme d'un angle
:
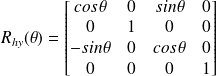
Une rotation autour de l'axe x s'écrit sous la forme d'un angle
:
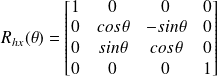
Rappel : Matrice de translation en coordonnées homogènes
Une matrice de translation en coordonnées homogènes s'écrit :
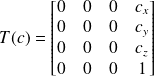
Définition : Matrice de passage et changement de repère en 3 dimensions
Les règles et les méthodes de calcul vue pour le plan s'appliquent de la même manière à 3 dimensions.
