Nous nous sommes en effet intéressés aux agrégats de carbone, au vu d'expériences récentes [40], et avons voulu leur appliquer les mêmes techniques qu'aux agrégats de sodium. Dans le cas du carbone, il est cependant indispensable d'utiliser des pseudopotentiels non-locaux ; nous avions de plus la contrainte de travailler avec des fonctions d'onde discrétisées sur une grille régulière en espace, comme nous en discuterons dans le chapitre suivant.
Un grand nombre d'auteurs ont proposé de tels pseudopotentiels, mais la
plupart sont prévus soit pour être utilisés en physique du solide, c'est
à dire avec des bases d'onde planes, soit en chimie quantique, donc avec
des bases de gaussiennes centrées sur les atomes constituant le système
moléculaire. La partie non-locale des pseudopotentiels
a été introduite pour tenir compte des effets des états de c![]() ur
sur les fonctions d'onde des électrons
de valence. Puisque les fonctions
d'onde des états de c
ur
sur les fonctions d'onde des électrons
de valence. Puisque les fonctions
d'onde des états de c![]() ur ne sont pas explicitement présentes, on
remplace cette condition d'orthogonalité par l'introduction d'un
potentiel répulsif proportionnel au résultat de l'application d'un projecteur
sur un état de c
ur ne sont pas explicitement présentes, on
remplace cette condition d'orthogonalité par l'introduction d'un
potentiel répulsif proportionnel au résultat de l'application d'un projecteur
sur un état de c![]() ur standard. Si on travaille avec des bases de
gaussiennes par exemple, ces projecteurs sont alors donnés dans ce type
de bases. La mise en
ur standard. Si on travaille avec des bases de
gaussiennes par exemple, ces projecteurs sont alors donnés dans ce type
de bases. La mise en ![]() uvre de ces pseudopotentiels avec nos méthodes
numériques s'est avérée malaisée. Cependant, Goedecker et ses
collaborateurs ont donné dans [41] des pseudopotentiels
non-locaux pour les éléments des trois premières lignes de la table
périodique, ces pseudopotentiels étant optimisés à la fois pour un usage
avec une grille régulière en espace comme avec une base d'onde planes.
Pour la partie locale de ce pseudopotentiel, les auteurs
de [41] ont choisi :
uvre de ces pseudopotentiels avec nos méthodes
numériques s'est avérée malaisée. Cependant, Goedecker et ses
collaborateurs ont donné dans [41] des pseudopotentiels
non-locaux pour les éléments des trois premières lignes de la table
périodique, ces pseudopotentiels étant optimisés à la fois pour un usage
avec une grille régulière en espace comme avec une base d'onde planes.
Pour la partie locale de ce pseudopotentiel, les auteurs
de [41] ont choisi :
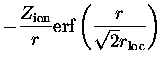 |
|||
![$\displaystyle e^{\displaystyle
-\frac{1}{2}
\left(
\frac{r}{r_{\mbox{\scriptsiz...
...}
\right)^4
+
C_4
\left(
\frac{r}{r_{\mbox{\scriptsize loc}}}
\right)^6
\right]$](img106.gif) |
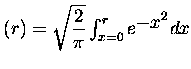 )
on reconnaît dans cette forme une partie qui se comporte comme un
potentiel coulombien à longue distance, le premier terme
(car
)
on reconnaît dans cette forme une partie qui se comporte comme un
potentiel coulombien à longue distance, le premier terme
(car
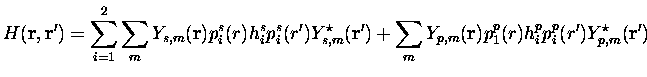
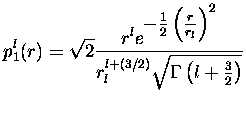
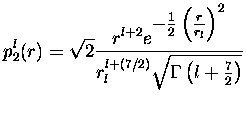
où ![]() est la fonction gamma telle que
est la fonction gamma telle que
![]() .
Ces projecteurs sont normalisés, et on voit que la partie non-locale
tend rapidement vers zéro à l'extérieur de la région de c
.
Ces projecteurs sont normalisés, et on voit que la partie non-locale
tend rapidement vers zéro à l'extérieur de la région de c![]() ur. De
plus, ils ont une forme similaire, et donc les mêmes propriétés en
espace réciproque. Ceci veut dire que l'intégration intervenant dans le
calcul de l'effet de
ur. De
plus, ils ont une forme similaire, et donc les mêmes propriétés en
espace réciproque. Ceci veut dire que l'intégration intervenant dans le
calcul de l'effet de
![]() peut être réduite à une petite région
autour de chaque atome :
peut être réduite à une petite région
autour de chaque atome :
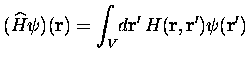 |
(10) |
Numériquement, avec le choix que nous avons fait de représenter les
fonctions d'onde sur une grille régulière en espace, l'usage de ces
pseudopotentiels non-locaux est donc à peine plus coûteux que l'usage de
pseudopotentiels locaux.
Nous avons réalisé plusieurs tests de précision de l'implantation
numérique que nous avons faite de ces pseudopotentiels.
Nous avons commencé par l'exemple le plus simple, l'atome d'hydrogène
(jusqu'au béryllium, tous les électrons interviennent et il n'y a pas
de partie non-locale dans les pseudopotentiels de [41]).
L'énergie totale a été reproduite à moins de 1% près avec une grille
de
![]() points espacés de 0.4
a
points espacés de 0.4
a![]() (voir le
chapitre suivant). Pour la molécule d'hydrogène dans son état
fondamental, la longueur de liaison correspond à celle donnée
dans [41] avec deux chiffres significatifs, longueur qui
elle-même diffère très peu du résultat expérimental.
(voir le
chapitre suivant). Pour la molécule d'hydrogène dans son état
fondamental, la longueur de liaison correspond à celle donnée
dans [41] avec deux chiffres significatifs, longueur qui
elle-même diffère très peu du résultat expérimental.
Nous avons considéré ensuite un système légèrement moins simple, l'atome
de béryllium (pour lequel, rappelons le, tous les électrons
interviennent et il n'y a pas de partie non-locale). Dans ce cas,
l'énergie totale de l'état fondamental de cet atome calculée sur une
grille de
![]() points espacés de 0.2
a
points espacés de 0.2
a![]() diffère de celle donnée dans [42]
de moins de 2%. Pour les
atomes de numéro atomique plus élevé, comme tous les électrons ne sont
plus pris en compte, on ne pourra plus comparer les énergies totales.
Par contre, les longueurs de liaison des molécules diatomiques ainsi
que les valeurs des énergies des niveaux Kohn-Sham peuvent constituer
un test pertinent de la validité des méthodes.
diffère de celle donnée dans [42]
de moins de 2%. Pour les
atomes de numéro atomique plus élevé, comme tous les électrons ne sont
plus pris en compte, on ne pourra plus comparer les énergies totales.
Par contre, les longueurs de liaison des molécules diatomiques ainsi
que les valeurs des énergies des niveaux Kohn-Sham peuvent constituer
un test pertinent de la validité des méthodes.
Ainsi, pour l'énergie de liaison en fonction de la distance
interatomique dans le cas du dimère de carbone ![]() dans un état
dans un état
![]() comparé aux calculs LDA de [43],
avec une grille
spatiale à trois dimensions de
comparé aux calculs LDA de [43],
avec une grille
spatiale à trois dimensions de ![]() points dans chaque direction,
espacés de
points dans chaque direction,
espacés de ![]() a
a![]() , on obtient même distance d'équilibre
et fréquence de vibration.
, on obtient même distance d'équilibre
et fréquence de vibration.
De même, nous comparons dans la table suivante les énergies des
orbitales Kohn-Sham occupées pour la molécule
N![]() dans son état
fondamental à sa distance d'équilibre, que nous trouvons correctement,
aux meilleurs résultats (c'est à dire, avec la base la plus étendue) LDA tous électrons
de [44]. Nous donnons ces résultats en eV soit pour la
fonctionnelle LSD de Gunnarson et Lundqvist [45] (GL76), soit pour
l'approximation par une fraction rationnelle à la fonctionnelle
Perdew-Wang 92 qui est utilisée par les auteurs de [41]
(PW92). Nos résultats ont été obtenus sur une grille de
dans son état
fondamental à sa distance d'équilibre, que nous trouvons correctement,
aux meilleurs résultats (c'est à dire, avec la base la plus étendue) LDA tous électrons
de [44]. Nous donnons ces résultats en eV soit pour la
fonctionnelle LSD de Gunnarson et Lundqvist [45] (GL76), soit pour
l'approximation par une fraction rationnelle à la fonctionnelle
Perdew-Wang 92 qui est utilisée par les auteurs de [41]
(PW92). Nos résultats ont été obtenus sur une grille de
![]() points espacés de 0.2
a
points espacés de 0.2
a![]() .
.
| rés. de [44] | GL76 | PW92 | |
| -28,33 | -28,84 | -29,05 | |
| -13,44 | -13,11 | -13,039 | |
| -11,08 | -11,50 | -11,39 | |
| -10.45 | -10,0 | -9,88 |
On peut voir que l'ordre de grandeur des fluctuations des résultats sur cette observable très fine est comparable à celles que les auteurs de [44] obtiennent en changeant de type de bases de gaussiennes. Pour le type de calcul que nous voulons faire, le résultat obtenu est donc tout à fait satisfaisant.