Un électron de valence d'un agrégat ressent de la part de ce que nous
appelons les << ions >> le potentiel du noyau atomique
(assimilé à une simple charge positive)et
l'effet des électrons de c![]() ur. Ces derniers écrantent le
potentiel coulombien créé par le noyau, et les exigences de la
mécanique quantique qui font que la fonction d'onde de l'électron de
valence doit être orthogonale aux états des électrons de c
ur. Ces derniers écrantent le
potentiel coulombien créé par le noyau, et les exigences de la
mécanique quantique qui font que la fonction d'onde de l'électron de
valence doit être orthogonale aux états des électrons de c![]() ur doivent
être pris en compte.
ur doivent
être pris en compte.
Dans un premier temps, nous avons introduit dans notre modèle les
pseudopotentiels de [38] pour le sodium. Ces pseudopotentiels
ne découlent pas de premiers principes, mais ont une forme physiquement
raisonnable et sont aisés à manipuler.
En effet, ils sont locaux,
ne s'influencent pas mutuellement, c'est à dire qu'un électron ressent
la superposition
![]() des pseudopotentiels créés par les ions, au nombre de
des pseudopotentiels créés par les ions, au nombre de
![]() et aux positions
et aux positions ![]() :
:
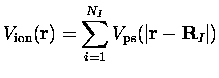
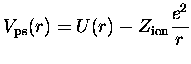
Afin de comparer les caractéristiques globales des pseudopotentiels,
nous employons la
<< force >>
![]() du pseudopotentiel.
Cette << force >>, introduite par Perdew et ses collaborateurs,
est définie comme la mesure de la
différence du pseudopotentiel avec un potentiel coulombien :
du pseudopotentiel.
Cette << force >>, introduite par Perdew et ses collaborateurs,
est définie comme la mesure de la
différence du pseudopotentiel avec un potentiel coulombien :
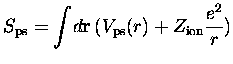
Nous avons constaté que la << force >> permettait de caractériser assez
bien en première approximation les pseudopotentiels, sur l'exemple des
configurations obtenues par une optimisation Monte-Carlo, supposant
une symétrie axiale du nuage des électrons de valence de
l'agrégat [38], qui de plus, comme les programmes
initialement développés l'avaient été dans le cadre du modèle du
<< jellium >> utilisaient une << pseudodensité ionique >> plutôt qu'un
pseudopotentiel. Il s'avère que dans le cadre du modèle du
<< jellium >> pour les agrégats de sodium, la densité de << jellium >> est très
proche à l'intérieur de l'agrégat de la densité électronique. Il vaut
donc mieux en pratique effectuer les calculs numériques sur la
différence des deux densités, plutôt que de soustraire les potentiels
obtenus à la fin des calculs. Reinhard et ses collaborateurs ont donc
défini cette pseudodensité
![]() comme
comme
Dans le programme sans symétrie que nous avons écrit au cours de cette thèse, nous avons pris une somme de deux gaussiennes pour la pseudodensité:
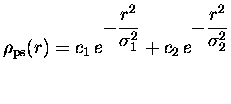
La force
![]() a cependant été déterminée
dans [38] à partir des propriétés macroscopiques du solide
de sodium, et, si elle donne des résultats acceptables pour la structure
des agrégats de sodium (bien que les dimensions des agrégats obtenues
par optimisation Monte-Carlo soient sous-estimées de quelques % par
rapport aux résultats obtenus avec les pseudopotentiels
de force 49,97 définis à l'annexe E), la position du pic plasmon qui en découle est
très nettement surestimée : dans notre cas test,
Na
a cependant été déterminée
dans [38] à partir des propriétés macroscopiques du solide
de sodium, et, si elle donne des résultats acceptables pour la structure
des agrégats de sodium (bien que les dimensions des agrégats obtenues
par optimisation Monte-Carlo soient sous-estimées de quelques % par
rapport aux résultats obtenus avec les pseudopotentiels
de force 49,97 définis à l'annexe E), la position du pic plasmon qui en découle est
très nettement surestimée : dans notre cas test,
Na![]() , pris
avec la configuration appelée 144 dans [38], on
trouve 3.2 eV au lieu d'un résultat expérimental de 2.73 eV, comme on
peut le voir sur la figure II.2 page
, pris
avec la configuration appelée 144 dans [38], on
trouve 3.2 eV au lieu d'un résultat expérimental de 2.73 eV, comme on
peut le voir sur la figure II.2 page ![[*]](cross_ref_motif.gif) .
Cette structure 144 est dessinée sur la figure III.1
page
.
Cette structure 144 est dessinée sur la figure III.1
page ![[*]](cross_ref_motif.gif) .
.
Nous avons par conséquent modifié les paramètres pour obtenir la force de la partie locale du pseudopotentiel donné dans [39] pour le sodium. Le résultat est bien meilleur, comme on peut le voir sur la figure III.3. La raison en est sans doute à trouver dans le fait que les pseudopotentiels de force 49,97 de l'annexe E ont été obtenus par un ajustement de leurs paramètres sur des résultats de chimie quantique pour des systèmes à un ou deux atomes, ce qui explique le fait que pour un petit agrégat on ait des résultats plus corrects qu'avec des paramètres obtenus par ajustement sur des résultats pour le solide infini.
M.Brack nous a de plus fait remarquer que la forme radiale des pseudopotentiels, et pas seulement leur <<force>>, était importante pour des observables comme la fréquence plasmon. Un travail important d'amélioration des pseudopotentiels locaux est donc encore nécessaire.
Le lecteur pourra se référer à l'annexe E pour plus de détails, en particulier pour les paramètres employés.
On peut remarquer sur les figures II.2 page ![[*]](cross_ref_motif.gif) et III.3 page
et III.3 page ![[*]](cross_ref_motif.gif) que les deux pics expérimentaux du spectre de photoabsorption sont
reproduits, ce qui montre que l'introduction d'une structure ionique
explicite est indispensable pour obtenir des résultats précis. Dans le
cas de
Na
que les deux pics expérimentaux du spectre de photoabsorption sont
reproduits, ce qui montre que l'introduction d'une structure ionique
explicite est indispensable pour obtenir des résultats précis. Dans le
cas de
Na![]() , en effet, nous avons déjà indiqué que le modèle
du << jellium >> adouci en surface donnait une position correcte du pic
plasmon, mais la structure la plus stable dans ce cas est une
sphère, et il n'apparaît jamais qu'un seul pic au voisinage de la
fréquence plasmon dans le spectre obtenu
avec ce modèle, même en tenant compte de l'interférence éventuelle du
pic plasmon avec les monoexcitations électroniques
car celles-ci ont une énergie éloignée de celle de la résonance plasmon
(voir l'introduction, le chapitre III et [19] pour
plus de précisions).
, en effet, nous avons déjà indiqué que le modèle
du << jellium >> adouci en surface donnait une position correcte du pic
plasmon, mais la structure la plus stable dans ce cas est une
sphère, et il n'apparaît jamais qu'un seul pic au voisinage de la
fréquence plasmon dans le spectre obtenu
avec ce modèle, même en tenant compte de l'interférence éventuelle du
pic plasmon avec les monoexcitations électroniques
car celles-ci ont une énergie éloignée de celle de la résonance plasmon
(voir l'introduction, le chapitre III et [19] pour
plus de précisions).
Les pseudopotentiels locaux que nous venons de décrire dans cette
section ne sont cependant sensés que pour des exemples précis comme le
sodium où il n'y a qu'un électron de valence par atome, autour d'un
c![]() ur électronique sphérique et difficilement polarisable, avec une bonne
approximation. Pour d'autres éléments que le sodium, sans même parler
de corrections relativistes, il faut cependant inclure les effets des
électrons de c
ur électronique sphérique et difficilement polarisable, avec une bonne
approximation. Pour d'autres éléments que le sodium, sans même parler
de corrections relativistes, il faut cependant inclure les effets des
électrons de c![]() ur par exemple par un opérateur non-local pour le
pseudopotentiel. De plus, pour obtenir des résultats fiables, il faut
que les pseudopotentiels employés présentent la propriété de
<< transférabilité >>.
ur par exemple par un opérateur non-local pour le
pseudopotentiel. De plus, pour obtenir des résultats fiables, il faut
que les pseudopotentiels employés présentent la propriété de
<< transférabilité >>.