Comparaison des spectres des différentes observables avec la RPA

Nous allons illustrer ceci sur un exemple comparant les résultats obtenus aux résultats de la RPA.

Figure: Spectre de puissance pour Na$_{44}^{4+}$, excité par un déplacement instantané dans l'espace des positions, pour deux énergies d'excitation, la première de 0.6 eV laissant le système dans le régime linéaire, la deuxième de 10 eV dans le régime multi-plasmon. La fonction de force obtenue par la RPA est également dessinée sur la partie inférieure de la figure ; on a attribué une largeur de 0.04 eV aux pics RPA pour plus de lisibilité. Tous les pics ont de plus été normalisés à la même valeur pour plus de lisibilité.

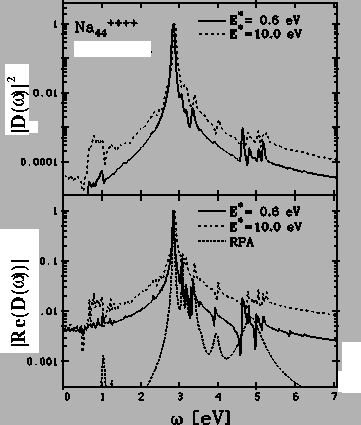
Sur la figure I.2, la partie inférieure représente la fonction de force pondérée en énergie obtenue par la RPA suivant la méthode présentée dans [20], comparée avec la partie réelle du spectre du moment dipolaire obtenu en symétrie axiale après excitation d'un agrégat Na$_{44}^{4+}$ par translation instantanée du nuage électronique dans l'espace des positions. Le fond ionique de l'agrégat est ici un << jellium >> sphérique et adouci, d'épaisseur de surface 1 a$_0$. Ce cas particulier a été choisi car la forte charge positive retient les électrons qui pourraient éventuellement quitter l'agrégat par suite de l'excitation. Ce problème est donc éliminé ; de plus, le choix d'un nombre magique d'électrons de valence implique que la structure ionique sous-jacente est sphérique, ce qui facilite le calcul en RPA. On a d'autre part choisi un agrégat de sodium de cette taille particulière, car la résonance plasmon se trouve à une énergie proche de certaines monoexcitations électroniques, ce qui va fragmenter le pic de résonance plasmon par suite de l'interférence avec ces monoexcitations [19,20]. On pourra alors vérifier que la résolution directe en temps des équations TDLDA fait ressortir cette fragmentation d'origine quantique aussi bien que la RPA.

Sur la partie inférieure de la figure, on voit que la résonance plasmon, qui se trouve à une position de 2.8 eV environ, est particulièrement marquée, ce qui rend nécessaire une échelle logarithmique pour faire ressortir les autres pics éventuels. Avec cette échelle, les résultats de la TDLDA non-linéarisée coïncident correctement dans le régime linéaire avec les résultats RPA, en particulier pour les hautes fréquences ; à basse énergie, le spectre TDLDA présente un bruit qui masque certains pics éventuels. Ce bruit trouve son origine dans le grand nombre d'itérations employées pour résoudre les équations de Kohn-Sham dépendant du temps sur un intervalle suffisant pour avoir une bonne résolution spectrale, dans le fait qu'une petite partie du nuage électronique quitte l'agrégat et élargit donc les pics, ou par le fait qu'il y a un léger désaccord entre l'ensemble discret de points employés pour calculer la transformée de Fourier du signal dipolaire et les fréquences physiquement présentes dans ce signal. Ce désaccord fait apparaître des << forces >> légèrement négatives dans le spectre, et oblige à tracer la valeur absolue de la << force >> $\widetilde{D}(\omega)$.

Dans le régime non-linéaire, on voit une légère augmentation du bruit de fond et un adoucissement des structures, mais celles-ci restent préservées malgré l'importance de l'énergie d'excitation.

Sur la partie supérieure de la figure I.2, on voit que le spectre de puissance filtré en temps fait encore plus ressortir les différents pics du signal. Leur importance relative est cependant mal mesurable avec cette observable.