Méthode FALR

Introduisons la notation $\rho \rightarrow \widetilde{\rho}$ pour la transformée de Fourier

$$\widetilde{\rho}({\bf k})=\int\limits_{-\infty}^{\infty}\frac{d{\bf r}} {(2\pi)^{3/2}}e^{i{\bf k.r}}\rho({\bf r})$$

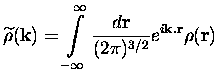
L'expression du Laplacien en espace de Fourier se réduit à une multiplication par $-k^{\:2}$. Malheureusement, une simple division de la transformée de Fourier $\widetilde{\rho}({\bf k})$ ne fournit pas le résultat qu'on aurait pu naïvement escompter pour résoudre l'équation, pour plusieurs raisons : d'abord, les moments multipolaires de $l<2$ de la distribution provoquent des ennuis numériques dans la division par $-k^{\:2}$ lorsque ${\bf k}\to 0$, car la grille est régulièrement espacée et qu'il est donc impossible de représenter correctement le comportement à l'origine, mais surtout le fait que la transformée de Fourier est discrétisée sur une grille finie induit que des répliques "fantômes" de la densité exercent un effet en $$\frac{1}{r}$$, donc qui diminue lentement avec la distance, depuis toutes les grilles répétées périodiquement dans toutes les directions de l'espace de par la finitude de la transformée de Fourier.

Reinhard et ses collaborateurs ont alors eu l'idée [55] de prendre avantage de la linéarité de l'équation de Poisson, et de traiter la contribution des moments multipolaires de $l$ le plus bas $l\leq 4$ semi-analytiquement, et le << reste >> numériquement par passage en espace de Fourier ce qui a le double avantage de supprimer la discontinuité pour $l<2$, et de réduire très fortement la contribution au potentiel des répliques << fantômes >> de la densité, puisque celles-ci n'exerceront plus qu'un potentiel en $$\frac{1}{r^5}$$ au moins. La procédure, qui a été baptisée << FALR >> (Fourier Analysis with Long Range forces) est donc la suivante :

• calcul des $q_{lm}$, moments multipolaires de $\rho$ pour $l\leq 4$
• soustraction de $\rho$ d'une densité arbitraire $\rho_l$ ayant les mêmes $q_{lm}$ que $\rho$
• calcul de la transformée de Fourier rapide (FFT) $\widetilde{\rho}({\bf k})$ de $\rho$

• calcul du potentiel $$\widetilde{\Phi}({\bf k})=\frac{\widetilde{\rho}({\bf k})}{k^{\:2}}$$
• calcul de la FFT inverse $\Phi({\bf r})$ de $\widetilde{\Phi}({\bf k})$
• ajout à $\Phi({\bf r})$ de la contribution du potentiel créé par $\rho_l$ soustraite au début. Cette contribution peut être calculée semi-analytiquement(une seule intégrale radiale demeure, voir [55] pour les détails).

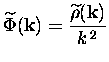
Cette méthode s'avère précise, rapide, et bénéficie de la robustesse des algorithmes basées sur la transformée de Fourier rapide (FFT). Nous l'avons donc adoptée dans la version à trois dimensions du code. Nous nous sommes cependant réservé la possibilité d'utiliser les sous-routines << FISHPACK >>, une très bonne implantation de la méthode SOR trouvée sur le serveur NETLIB, qui présente de plus l'avantage de pouvoir résoudre l'équation de Helmholtz qui intervient pour calculer le potentiel de Yukawa en physique nucléaire.

Disposant de méthodes efficaces pour résoudre l'équation de Poisson qui intervient aussi bien dans la partie statique que dynamique des codes, nous pouvons aborder désormais ces problèmes.