État fondamental

Avant de simuler dans le domaine temporel la réponse des électrons de valence de l'agrégat métallique, il faut connaître l'état fondamental de celui-ci. Dans le formalisme que nous avons choisi, pour une configuration ionique donnée, cela revient à résoudre les équations de Kohn-Sham statiques I.2. Celles-ci, au degré de liberté de spin près dans la cas où la LSD est appliquée, peuvent se résumer avec nos notations à l'ensemble d'équations monoélectroniques :

$$\widehat{h} \psi _i = \epsilon _i \psi _i$$

avec

$$\widehat{h} = - \frac{\hbar^{\:2}}{2m_{el}} \Delta + \widehat{V}_{\mbox{\scriptsize ext}} + \Phi({\bf r}) + v_{\mbox{\scriptsize xc}}({\bf r})$$

Ici, $\widehat{V}_{\mbox{\scriptsize ext}}$ se résume au pseudopotentiel créé par les ions. Ces équations sont autocohérentes car $\Phi$ et $v_{\mbox{\scriptsize xc}}$ dépendent de la densité, qui dépend directement des $\psi_i$ : le Hamiltonien monoélectronique est un opérateur non-linéaire.

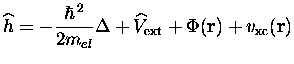
Pour le terme d'énergie cinétique, qui ne peut être évalué exactement, il faudra s'efforcer dans un souci de cohérence de prendre pour le calculer le même opérateur que celui qui servira dans le calcul dynamique : on verra que dans nos travaux, cela correspond soit à un opérateur aux différences finies, soit à un passage en espace de Fourier par FFT, car, comme nous l'avons déjà fait remarquer à propos de la résolution de l'équation de Poisson, le Laplacien se réduit alors à une multiplication par $-k^{\:2}$.

Vu son caractère autocohérent, une procédure itérative semble la plus naturelle pour résoudre cet ensemble d'équations.