


Next: Méthode SOR
Up: Aspects numériques et parallélisation
Previous: Représentation des fonctions d'onde
Table des matières
Le problème de la résolution de l'équation de Poisson se pose aussi bien
dans le calcul de l'état fondamental I.2 que dans la résolution des
équations dynamiques I.6, et ce sous la même forme : trouver 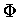 ,
potentiel de Hartree tel que
,
potentiel de Hartree tel que
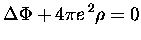 |
(12) |
où 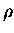 est normalement la densité électronique seule, mais peut aussi
être, dans le but d'avoir des résultats légèrement plus précis dans le
cadre du modèle du << jellium >>, la différence de cette densité et de la
densité de << jellium >> ou de la pseudodensité ionique comme nous
l'expliquions dans le chapitre précédent page
est normalement la densité électronique seule, mais peut aussi
être, dans le but d'avoir des résultats légèrement plus précis dans le
cadre du modèle du << jellium >>, la différence de cette densité et de la
densité de << jellium >> ou de la pseudodensité ionique comme nous
l'expliquions dans le chapitre précédent page ![[*]](cross_ref_motif.gif) .
.
Il est indispensable de passer par la résolution de cette équation, car
l'intégration directe :
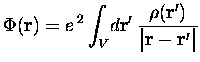 |
(13) |
est trop lourde numériquement si effectuée en chaque point de la boîte.
Nous allons exposer les deux méthodes que nous avons principalement
employées dans dans cette thèse.



Next: Méthode SOR
Up: Aspects numériques et parallélisation
Previous: Représentation des fonctions d'onde
Table des matières
Florent Calvayrac
1999-05-05
![]() ,
potentiel de Hartree tel que
,
potentiel de Hartree tel que
![[*]](cross_ref_motif.gif) .
.