La faute en est aux parties des fonctions d'onde qui ont une énergie cinétique trop grande, qui ralentissent la convergence. Reinhard et ses collaborateurs ont proposé une méthode pour remédier à ce problème, la << méthode du gradient amorti >> (damped step gradient method, [57,51]). Cette méthode est essentiellement une amélioration de la méthode du pas de temps imaginaire, où le terme d'énergie cinétique intervenant dans les équations à un corps I.2 est amorti pour les énergies les plus grandes. Le pas s'écrit alors pour passer d'une étape à la suivante du schéma itératif:
![]() signifie l'orthonormalisation de toutes les
signifie l'orthonormalisation de toutes les ![]() ,
,
![]() , le Hamiltonien étant
fonctionnelle des
, le Hamiltonien étant
fonctionnelle des
![]() et
et
![]() est un opérateur d'amortissement
est un opérateur d'amortissement
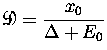
où ![]() et
et ![]() sont des paramètres numériques, correspondant à la
taille du pas de temps et à la force de l'amortissement des termes de
haute énergie cinétique. Dans le cas où cette énergie cinétique est
calculée en espace de Fourier, l'application de ce pas de gradient
amorti est immédiate, sinon elle nécessite l'inversion d'un opérateur.
L'orthonormalisation des fonctions d'onde à chaque pas de temps est
quelque peu coûteuse numériquement : en effet, elle est effectuée par le
procédé de Schmidt, sur lequel nous reviendrons à propos de la
parallélisation des méthodes. Nous sommes conscients qu'il existe des
procédés plus stables numériquement car plus équilibrés, mais pour un
nombre de fonctions d'onde dans le système qui n'est pas trop grand, ce
schéma reste le plus efficace.
sont des paramètres numériques, correspondant à la
taille du pas de temps et à la force de l'amortissement des termes de
haute énergie cinétique. Dans le cas où cette énergie cinétique est
calculée en espace de Fourier, l'application de ce pas de gradient
amorti est immédiate, sinon elle nécessite l'inversion d'un opérateur.
L'orthonormalisation des fonctions d'onde à chaque pas de temps est
quelque peu coûteuse numériquement : en effet, elle est effectuée par le
procédé de Schmidt, sur lequel nous reviendrons à propos de la
parallélisation des méthodes. Nous sommes conscients qu'il existe des
procédés plus stables numériquement car plus équilibrés, mais pour un
nombre de fonctions d'onde dans le système qui n'est pas trop grand, ce
schéma reste le plus efficace.
Dans la majorité des cas, lorsque l'estimation initiale est judicieusement choisie, ce schéma itératif converge en quelques dizaines d'itérations.