On peut prouver en effet que la fonction d'onde multiélectronique de
l'état fondamental d'un système fictif sans interaction soumis
au potentiel extérieur de Kohn-Sham tel qu'il est défini dans
l'annexe A peut s'exprimer simplement comme
un produit antisymétrisé de fonctions d'onde
monoélectroniques ![]() obéissant à l'ensemble d'équations de
Schrödinger :
obéissant à l'ensemble d'équations de
Schrödinger :
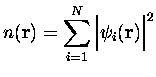 |
(3) |
| (4) |
Ces équations à un corps sont
appelées équations de Kohn-Sham. Elles sont couplées et non-linéaires car
le potentiel
![]() y dépend de la densité. Ces
équations peuvent néanmoins être résolues par une procédure
autocohérente que nous décrirons page
y dépend de la densité. Ces
équations peuvent néanmoins être résolues par une procédure
autocohérente que nous décrirons page ![[*]](cross_ref_motif.gif) . Il est à noter que
les équations obtenues sont de la forme de Hartree ; il n'y a pas
d'opérateur non-local du type Fock qui intervienne, ce qui simplifie
les calculs. La seule approximation porte sur le terme
d'échange-corrélation
. Il est à noter que
les équations obtenues sont de la forme de Hartree ; il n'y a pas
d'opérateur non-local du type Fock qui intervienne, ce qui simplifie
les calculs. La seule approximation porte sur le terme
d'échange-corrélation
![]() qui n'est pas connu
exactement. Nous recourrons à l'approximation
locale (LDA)
où
qui n'est pas connu
exactement. Nous recourrons à l'approximation
locale (LDA)
où
![]() est simplement une fonction de la densité au point
est simplement une fonction de la densité au point ![]() , donc ce
qu'on appellera une fonctionnelle locale.
Nous donnons plus de détail à ce sujet dans l'annexe A.
, donc ce
qu'on appellera une fonctionnelle locale.
Nous donnons plus de détail à ce sujet dans l'annexe A.