Méthodes de Crank-Nicholson et Peaceman-Rachford

La première catégorie de méthodes que nous avons employées est basée sur les techniques appliquées dans les travaux de physique nucléaire à l'origine de notre travail [49,50,51,58]. Les équations Hartree-Fock dépendant du temps y étaient résolues par une approximation séparable à la méthode de Crank-Nicholson, la méthode de Peaceman-Rachford. La méthode de Crank-Nicholson consiste à écrire pour passer de $\psi_i(t)$ à $\psi_i(t+\Delta t \,)$, où $\Delta t \,$ est le pas de temps

$$\psi_i(t+\Delta t \,) = [1+\frac{i}{2\hbar}\Delta t \,\:\widehat{h}]^{-1} [1-\frac{i}{2\hbar}\Delta t \,\:\widehat{h}] \psi_i(t)$$ (16)

Cette méthode, faisant partie de la classe des méthodes implicites car supposant le calcul de $\psi_i(t+\frac{\textstyle\Delta t}{\textstyle 2})$, présente plusieurs avantages : elle est explicitement unitaire, comme l'opérateur d'évolution exact II.4, ce qui garantit contre une perte non-physique de masse par variation de la normalisation des fonctions d'onde, et rend cette méthode inconditionnellement stable.

D'autre part, si l'opérateur d'énergie cinétique $\widehat{t}$ est approché par un opérateur aux différences finies, et qu'on suppose la valeur des fonctions d'onde nulle à l'extérieur de la boîte où les calculs sont effectués, le calcul de l'application de l'opérateur inverse $[1+\frac{i}{2}\Delta t \,\widehat{h}]^{-1}$, qui peut se ramener évidemment à une résolution d'un système linéaire, est extrêmement simplifié car la méthode du pivot de Gauss donne de proche en proche les valeurs de $\psi_i(t+\Delta t \,)$ pour un coût à peine supérieur à celui de la méthode d'Euler et une précision bien meilleure.

Dans des systèmes à plus d'une dimension l'inversion intervenant dans le pas de temps Crank-Nicholson est cependant rapidement pénalisante. On peut alors scinder le pas par une approximation supplémentaire, la méthode de Peaceman-Rachford. Cette méthode consiste à scinder la propagation dans des directions d'espace différentes. Dans les cas où nous supposons une symétrie axiale pour le nuage électronique, ce pas de temps s'écrit

$$\psi_i(t+\Delta t \,) = [1+\frac{i}{2\hbar}\Delta t \,\widehat{h}_v]^{-1} [1+\frac{i}{2\hbar}\Delta t \,\widehat{h}_h]^{-1}$$

$$[1-\frac{i}{2\hbar}\Delta t \,\widehat{h}_h] [1-\frac{i}{2\hbar}\Delta t \,\widehat{h}_v] \psi_i(t)$$

Le Hamiltonien monoélectronique $\widehat{h}$ étant séparé en ses contributions suivant les deux axes :

$$\widehat{h}=\widehat{h}_v+\widehat{h}_h$$

la partie potentielle étant répartie à parts égales entre les deux directions.

En trois dimensions, ce schéma peut s'écrire

$$\psi_i(t+\Delta t \,) = [1+\frac{i}{2\hbar}\Delta t \,\widehat{h}_x]^{-1} [1+\frac{i}{2\h... ...Delta t \,\widehat{h}_y]^{-1} [1+\frac{i}{2\hbar}\Delta t \,\widehat{h}_z]^{-1}$$

$$[1-\frac{i}{2\hbar}\Delta t \,\widehat{h}_z] [1-\frac{i}{2\hbar}\Delta t \,\widehat{h}_y] [1-\frac{i}{2\hbar}\Delta t \,\widehat{h}_x] \psi_i(t)$$

où

$$\widehat{h}_i=\widehat{t}_i+\frac{\displaystyle V(t)}{3}$$

avec $i$ qui représente une des directions $x$,$y$,$z$.

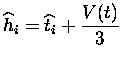
Un problème demeure cependant : puisque le Hamiltonien dépend du temps non seulement par l'introduction éventuelle d'une perturbation extérieure dépendant du temps (par exemple un champ laser femtoseconde) mais aussi via la dépendance en la densité électronique $n({\bf r},t)$, il faut introduire une autocohérence en temps ; le $\widehat{h}$ qui intervient dans toutes les équations ci-dessus dans le cadre de la méthode de Crank-Nicholson et ses variantes est pris à $t+\frac{\Delta t}{2}$, et il faut donc estimer $\widehat{h}(t+\frac{\Delta t}{2})$ par exemple par un procédé itératif. Nous avons choisi de calculer une valeur approchée de $\psi_i(t+\Delta t \,)$ à l'aide de $\widehat{h}(t)$, d'en déduire

$$\psi_i(t+\frac{\Delta t \,}{2})\approx\frac{\displaystyle \psi_i(t)+\psi_i(t+\Delta t \,)}{2}$$

d'où un $\widehat{h}(t+\frac{\Delta t \,}{2})$ approché, un $\psi_i(t+\Delta t \,)$ plus précis, et ainsi de suite suffisamment de fois pour stabiliser le processus. En pratique, deux ou trois itérations sont nécessaires pour ce faire.

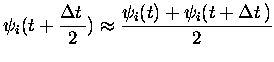
Dans l'implantation de la méthode à deux dimensions issue de la physique nucléaire dont nous disposions au début de cette thèse, la résolution des systèmes linéaires était effectuée explicitement. Dans la version à trois dimensions que nous avons écrite, nous avons fait usage des bibliothèques d'algèbre linéaire BLAS et LAPACK pour réaliser les inversions de systèmes linéaires tridiagonaux(l'approximation aux différences partielles à trois points était utilisée). Quelques précautions ont été à prendre lors de l'écriture des matrices tridiagonales à cause des conditions aux limites ; de plus, il a fallu successivement installer $x$,$y$ et $z$ comme dimensions intérieures des champs afin de pouvoir écrire les matrices tridiagonales sous forme compacte.

Le coût de la méthode en trois dimensions reste donc assez élevé, et oblige à l'emploi d'une approximation aux différences finies pour l'opérateur d'énergie cinétique. Nous nous sommes donc tournés vers une méthode basée sur un calcul du Laplacien par passage en espace de Fourier.