Ayant calculé l'état fondamental de l'agrégat pour une configuration
ionique donnée, il faut résoudre les équations de Kohn-Sham
dépendant du temps I.6 sur un intervalle de temps suffisamment
long pour obtenir assez d'informations sur les propriétés spectrales du
système. Dans le cas-type que nous étudions, l'agrégat
Na![]() ,
qui a une fréquence plasmon aux alentours de 3 eV , il est indispensable
d'avoir accès aux valeurs du moment dipolaire
,
qui a une fréquence plasmon aux alentours de 3 eV , il est indispensable
d'avoir accès aux valeurs du moment dipolaire ![]() sur au moins 60 fs pour avoir une résolution acceptable dans le domaine
fréquentiel.
sur au moins 60 fs pour avoir une résolution acceptable dans le domaine
fréquentiel.
Ici aussi, nous emploierons une méthode itérative, partant de la condition initiale éventuellement excitée et appliquant un schéma itératif avec un Hamiltonien comportant éventuellement un terme dépendant du temps pour obtenir les valeurs des observables sur l'intervalle de temps voulu.
Dans tous les cas, nous prenons les équations de Kohn-Sham dépendant du temps I.6, qui peuvent s'écrire dans l'approximation adiabatique, le degré de liberté de spin éventuel étant sous-entendu
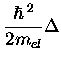 et
et