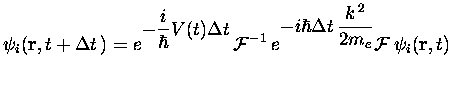 |
(17) |
Cette méthode, dont la formalisation que nous allons donner est due à P.-G. Reinhard, ainsi que la petite démonstration qui suit, existe sous un grand nombre de formes similaires. On peut par exemple citer les travaux de [59] sur la résolution de l'équation de Schrödinger non-linéaire, qui pose sous une forme simplifiée la plupart des problèmes qui se présentent dans ce travail.
L'idée consiste à séparer la propagation en contributions dues aux termes cinétiques et potentiels, qui pourra être exprimée dans chaque cas par des exponentielles exactes.
Le pas de temps se réduit alors au premier ordre à
Il est cependant possible d'écrire un pas de temps au deuxième ordre pour un coût très légèrement supérieur.
Si nous considérons en effet le pas de temps :
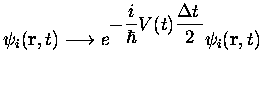
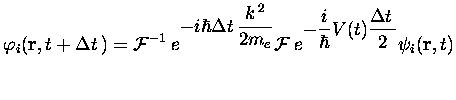
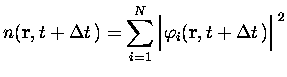
Il reste à prouver que le pas de temps est bien d'ordre deux.
Développons l'intégrale intervenant dans le pas de temps exact II.4 à cet ordre :
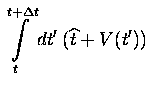 |
![$\displaystyle \Delta t \, \widehat{t}
+
\frac{1}{2}\left[
\Delta t \, V(t) + \f...
... \, V(t+\Delta t \,) - \frac{\Delta t^{\:2}}{2} \dot{V}
(t+\Delta t \,)
\right]$](img246.gif) |
||
![$\displaystyle \Delta t \,\widehat{t} +
\frac{1}{2}\left[ \Delta t \, V(t) +\Delta t \, V(t+\Delta t \,) \right]$](img247.gif) |
En portant ce résultat dans II.4 :
où
![]() désigne le commutateur, les temps auxquels
désigne le commutateur, les temps auxquels
![]() et
et ![]() sont pris n'intervenant pas à cet ordre.
sont pris n'intervenant pas à cet ordre.
Quant au pas de temps II.7, on peut le développer au deuxième ordre
en
ce qui est identique au résultat de II.8. Le pas de
temps II.7 est donc bien d'ordre deux.
Du point de vue de la rapidité, le pas de temps II.7 semble être
plus lent que celui de II.6, car il nécessite deux évaluations du
terme potentiel, en ![]() et
et
![]() . Ces évaluations sont assez
onéreuses numériquement à cause de la résolution de l'équation de
Poisson qui y est nécessaire. Cependant, on peut remarquer
que
. Ces évaluations sont assez
onéreuses numériquement à cause de la résolution de l'équation de
Poisson qui y est nécessaire. Cependant, on peut remarquer
que
![]() est utilisé deux fois, une fois à la fin du pas de
temps de
est utilisé deux fois, une fois à la fin du pas de
temps de ![]() à
à
![]() , et une fois au début du pas de temps
suivant. On peut donc utiliser un pas de temps asymétrique
, et une fois au début du pas de temps
suivant. On peut donc utiliser un pas de temps asymétrique
avec
![]() et
et
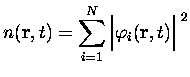
Toutefois, lorsque les observables physiques devront être évaluées, il faudra bien entendu passer par les << vraies >> fonctions d'onde
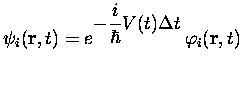
Finalement, nous disposons d'un schéma itératif pour résoudre les équations TDKS II.3 qui présente un grand nombre d'avantages : il est d'ordre deux, ne requiert qu'une évaluation du potentiel par pas de temps, ce qui le prend très similaire à la méthode << leap-frog >> pour résoudre les équations du mouvement de points matériels en interaction. De plus, il est exactement unitaire donc inconditionnellement stable, ce qui est un avantage par rapport aux algorithmes utilisant un développement en série pour calculer l'exponentielle des opérateurs. Grâce à l'usage de transformées de Fourier, l'énergie cinétique y est en outre évaluée de manière plus précise et plus stable que dans toutes les méthodes basées sur l'utilisation d'opérateurs aux différences finies.