- ...
l'électron-volt.
![[*]](foot_motif.gif)
- Pour les unités, voir le tableau de l'annexe D
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... métal.
![[*]](foot_motif.gif)
- Le rayon de Wigner-Seitz vaut 3.96
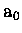 pour le sodium, et il
faut remarquer que cette valeur est particulièrement proche de la valeur
(4.04
pour le sodium, et il
faut remarquer que cette valeur est particulièrement proche de la valeur
(4.04 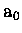 lorsque la fonctionnelle de Gunnarson-Lundqvist est
utilisée) pour laquelle l'énergie de
cohésion d'un métal infini est minimale dans
le modèle du << jellium >>. C'est un argument pour expliquer le succès particulier de ce
modèle pour le sodium.
lorsque la fonctionnelle de Gunnarson-Lundqvist est
utilisée) pour laquelle l'énergie de
cohésion d'un métal infini est minimale dans
le modèle du << jellium >>. C'est un argument pour expliquer le succès particulier de ce
modèle pour le sodium.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... effectués,
![[*]](foot_motif.gif)
- Ceci a l'inconvénient d'insérer automatiquement des conditions
aux limites réfléchissantes, ce qui obligera à prendre des boîtes un peu
plus grandes qu'avec d'autres méthodes, comme nous l'avons évoqué plus
haut, à moins d'insérer des conditions aux limites absorbantes
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... spin
![[*]](foot_motif.gif)
- des
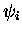 de spin
différents sont déjà orthogonales, la parallélisation du POS est donc
triviale dans ce cas
de spin
différents sont déjà orthogonales, la parallélisation du POS est donc
triviale dans ce cas
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quelconque
![[*]](foot_motif.gif)
- Le cas d'une perturbation brutale à l'instant initial est donc inclus dans le
formalisme
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Hohenberg-Kohn
![[*]](foot_motif.gif)
- il n'existe pas encore de forme satisfaisante de la théorie
de la fonctionnelle de la densité dépendant du temps du type de celle de
Lévy dans le cas statique
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)
![[*]](foot_motif.gif)