Adaptation aux pseudopotentiels non-locaux

Le schéma itératif qui vient d'être présenté est particulièrement avantageux car l'opérateur potentiel y est local en espace direct, et celui d'énergie cinétique local en espace de Fourier. Cependant, lorsqu'il est fait usage d'opérateurs non-locaux dans les pseudopotentiels, qui sont non-locaux dans les deux espaces, il faut modifier les méthodes employées.

Nous avons trouvé dans la littérature un article [56] proposant une adaptation de la méthode de Crank-Nicholson à un tel problème où interviennent des opérateurs non-locaux et non-linéaires dans le sens qu'ils dépendent des fonctions d'onde. Cette méthode, pour être précise, s'est avérée extrêmement coûteuse numériquement dans notre cas.

Malgré les inconvénients de la non-unitarité exacte qu'il implique, nous avons procédé à un développement en série de l'exponentielle de la partie non-locale des pseudopotentiels. Formellement, si nous notons $\widehat{P}_{\mbox{\scriptsize nl}}$ cet opérateur qui se rajoute au Hamiltonien monoélectronique :

$$\widehat{h}=\widehat{t}+V[n({\bf r},t),t]+\widehat{P}_{\mbox{\scriptsize nl}}$$

le pas de temps II.9 devient

$$\varphi_i({\bf r},t+\Delta t \,) = {\cal F}^{-1}\: e^{\displaystyle-i\hbar\Delta t \,\frac{k^{\:2}}{... ...:2}}\widehat{P}_{\mbox{\scriptsize nl}}^{\:2}\frac{\Delta t ^{\:2}}{2}+\cdots )$$

$$\times\quad e^{\displaystyle-\frac{i}{\hbar}V(t)\Delta t \,} \varphi_i({\bf r},t)$$

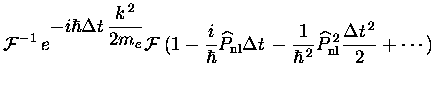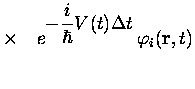En pratique, dans les cas que nous avons considérés, il s'est avéré suffisant d'arrêter le développement à l'ordre trois. La perte d'unitarité des fonctions d'onde est dans ce cas très faible lors de l'évolution en temps, car de toute façon $\widehat{P}_{\mbox{\scriptsize nl}}$ n'agit que dans des petites régions de l'espace. L'amélioration de la précision de la conservation de l'énergie totale au cours du temps lors de l'inclusion de termes supplémentaires dans le développement est néanmoins spectaculaire.