Quelques tests de précision

Quelques exemples simples vont nous permettre d'illustrer la bonne tenue numérique des techniques choisies, en mettant en évidence les différences entre les différentes techniques de propagation.

Dans un premier temps, nous allons vérifier la précision des méthodes qui viennent d'être discutées. Nous donnons sur la figure II.2 des résultats calculés pour le cas test récurrent de ${\rm Na}_9^+$ avec la configuration CAPS 144, avec les pseudopotentiels de [38]. Dans ces calculs, le nuage électronique a été excité par une translation instantanée suivant un axe diagonal par rapport aux axes principaux de l'agrégat, pour des raisons qui sont détaillées dans le chapitre suivant, où les différents modes d'excitation sont étudiés séparément. Cette structure est dessinée sur la figure III.1 page .

L'amplitude de l'excitation a été choisie soit pour que le nuage électronique reste proche de son état fondamental (régime linéaire, énergie d'excitation de 0.1 eV), ou pour qu'il soit loin de l'équilibre (régime non-linéaire, énergie d'excitation de 4.5 eV). La grille choisie pour le calcul était de 48 points dans chaque direction, espacés de 0.8 a$_0$. Le pas de temps était de 0.15 unités pour les deux techniques de propagation, qui faisaient usage soit de différences finies (méthode de Peaceman-Rachford), soit de passage en espace de Fourier pour calculer l'effet des opérateurs différentiels, les deux méthodes étant présentées dans le chapitre précédent.

Figure II.2: Test de précision de la dynamique électronique dans le cas de ${\rm Na}_9^+$ avec la configuration CAPS 144. À gauche, évolution de l'énergie totale au cours du temps, pour une excitation dans le régime linéaire comme non-linéaire. À droite, spectres de puissance normalisés obtenus dans le régime linéaire pour une excitation suivant la diagonale (1,1,1), avec les deux méthodes de propagation. Les moments dipolaires ont subi un filtrage dans le domaine temporel.

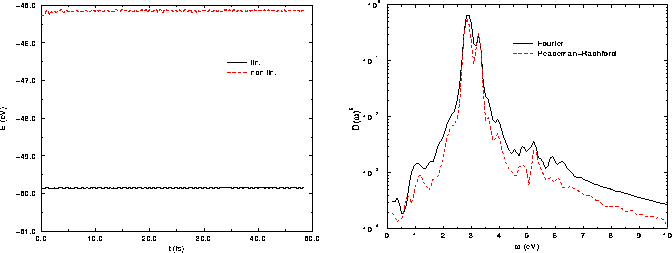
On voit que la conservation de l'énergie totale au cours du temps est très bien vérifiée dans les deux cas présentés, quoiqu'un peu moins bonne dans le cas non-linéaire que dans l'autre : de 0.01% dans le cas linéaire, et 0.1 % dans le cas non-linéaire. Ceci permet de résoudre la dynamique électronique sur des intervalles de temps suffisamment longs pour avoir une précision acceptable sur les spectres qui seront déduits des signaux temporels.

Ces spectres (ici, le spectre de puissance) sont tracés pour les deux méthodes sur la partie de droite de la figure II.2, pour une simulation calculée sur un intervalle de temps de 48 fs. Ici, l'observable temporelle considérée est le moment dipolaire du nuage électronique suivant la direction d'excitation, et ce moment a été calculé dans toute la boîte de calcul (et pas dans une zone d'analyse) pour faire ressortir les effets éventuels dûs aux différentes conditions aux limites. On ne peut donc vraiment comparer les spectres obtenus par les deux méthodes ; il faudrait pour cela qu'il y ait les mêmes conditions aux limites. Ceci pourrait être imposé par l'usage des mêmes conditions aux limites absorbantes dans les deux calculs, mais alors l'énergie ne serait pas exactement conservée au cours du temps, et le test de précision serait biaisé. L'atténuation des différences dûes aux conditions aux limites par l'usage de conditions absorbantes est mise en évidence sur la figure I.4 page .

La propagation alternée suivant les différentes directions d'espace de la méthode de type Peaceman-Rachford est légèrement plus coûteuse numériquement que la méthode en espace de Fourier, nous allons nous tenir à cette dernière pour les calculs en trois dimensions.