Comparaison à d'autres travaux

Dans un premier temps, nous allons comparer nos résultats à ceux obtenus en 1991 par Landman et ses collaborateurs [52]. Ces derniers avaient simulé la fission d'un agrégat Na$_4^{++}$, par une dynamique moléculaire adiabatique pour les ions sur la surface de potentiel Born-Oppenheimer, les électrons de valence de l'agrégat étant décrits sur une grille tridimensionnelle de façon tout à fait similaire à ce qui est présenté ici. Notre but est cependant d'étudier une dynamique couplée des électrons et des ions, en supprimant l'approximation adiabatique qui consiste à supposer que les électrons de valence sont à chaque instant dans l'état fondamental correspondant à la géométrie ionique à cet instant.

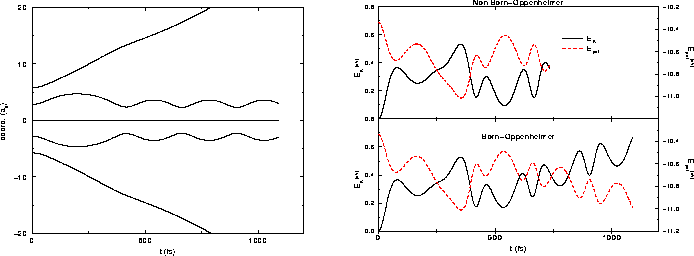
Nous présentons donc sur la figure III.9 un comparaison des résultats obtenus avec l'approximation Born-Oppenheimer ou sans cette approximation. La situation étudiée est très proche de celle de  [52]; la condition initiale auxiliaire est un agrégat Na$_4$, pris avec une géométrie de losange, subissant à l'istant initial de la simulation une excitation modélisée par une double ionisation qui enlève instantanément les fonctions d'onde d'énergie les plus élevées : toute l'énergie d'excitation fournie au système sert à l'ioniser. L'agrégat Na$_4^{++}$ résultant est instable, (les agrégats de sodium doublement chargés sont instables vis à vis de la fission jusqu'à une taille de 27 atomes), et les résultats de dynamique moléculaire présentés sur la figure III.9 ont été obtenus avec cette condition initiale.

Figure: Comparaison de calculs Born-Oppenheimer/non Born-Oppenheimer pour l'évolution de l'agrégat Na$_4^{++}$. La géométrie initiale est celle de Na$_4$ (losange) et les deux fonctions d'onde d'énergie les plus élevées sont supprimées à $t=0$. Les coordonnées cartésiennes des ions, superposables dans les résultats des deux calculs, sont tracées dans la partie gauche de la figure, et l'énergie électronique ainsi que l'énergie cinétique des ions sont tracées à droite. Les fonctions d'onde sont représentées dans une boîte de $24\times 24\times 24$ points espacés de 1 a$_0$, le pas de temps électronique est de 0.15 unités, et de 40 fois plus pour les ions, qui agissent par des pseudopotentiels ayant la force de [38]. Les équations I.11 sont utilisées.

On voit sur la figure III.9 que les dynamiques Born-Oppenheimer comme non-Born-Oppenheimer donnent exactement le même résultat, c'est à dire une explosion rapide en trois morceaux, un dimère Na$_2$ qui reste seul dans la boîte et vibre transversalement, et deux ions Na$^+$ qui sortent de la boîte de calcul. Ces résultats sont tout à fait comparables aux résultats originaux de [52].

Les deux méthodes donnent le même résultat car le nuage électronique se trouve à l'instant initial de la dynamique moléculaire dans son état fondamental. Les arguments de l'approximation Born-Oppenheimer sont valables ici et confirmés par le calcul non-Born-Oppenheimer : de pas de temps en pas de temps, les ions bougent car leur géométrie n'est pas stable, mais les fonctions d'onde électroniques suivent adiabatiquement ce changement de géométrie.

Ceci ne sera sûrement plus le cas si à l'instant initial le nuage électronique se trouve dans un état excité quelconque. Alors, il pourra y avoir échange d'énergie entre degrés de liberté ioniques et électroniques, avec conservation de l'énergie totale avec nos méthodes où la dynamique des électrons de valence est résolue en temps, ce qui ne serait pas vrai avec une simulation Born-Oppenheimer.