LDA-LSD

L'approximation la plus simple pour cette fonctionnelle d'échange-corrélation est en effet celle où $v_{\mbox{\scriptsize xc}}[n({\bf r})]$ est simplement une fonction de la densité au point ${\bf r}$, donc ce qu'on appellera une fonctionnelle locale.

La théorie de la fonctionnelle de la densité montre que le potentiel d'échange-corrélation dépend uniquement de la densité électronique. Les approximations à ce potentiel sont cependant nettement meilleures si on fait usage des densités de spin, ce qui est la manière la plus aisée de tenir compte des règles de Hund. On obtient alors l'approximation LSD (Local Spin Density), et la fonctionnelle d'échange-corrélation s'écrit

$$E_{\mbox{\scriptsize xc}}^{\mbox{\scriptsize LSD}}[n({\bf r})] = ... ...mbox{\scriptsize xc}} \left[ n_\uparrow({\bf r}), n_\downarrow({\bf r}) \right]$$ (31)

où $n_{\uparrow}({\bf r})$ est la densité d'électrons de spin-up et $n_{\downarrow}({\bf r})$ de spin-down.

La plupart des paramétrisations de ces fonctionnelles LSD ont été obtenues en calculant exactement l'énergie d'un gaz d'électrons infini pour différentes densités données.

Nous avons, dans la majorité des cas présentés dans cette thèse, utilisé la paramétrisation de Gunnarson et Lundqvist [45]. A titre documentaire, nous allons donner celle-ci, en unités naturelles de Hartree ($e^2=2.0$), en utilisant le fait que la fonctionnelle d'énergie peut être réécrite dans le cas polarisé en spin :

$$E_{{\rm xc}} = \int\! d{\bf r}\, n({\bf r})\left[\epsilon_{{\rm xc},p}\left(1-g(\xi)\right) +\epsilon_{{\rm xc},f}g(\xi)\right]$$ (32)

$$g(\xi) = \frac{(1+\xi)^{4/3}+(1-\xi)^{4/3}-2}{2^{4/3}-2}$$

$$n({\bf r}) = n_{\uparrow}({\bf r})+n_{\downarrow}({\bf r})$$

$$\xi = \frac{n_{\uparrow}({\bf r})-n_{\downarrow}({\bf r})}{n({\bf r})}$$

La fonction $g(\xi)$ permet un mélange approprié des contributions paramagnétiques ($p$-) et ferromagnétiques ($f$-).

$$\epsilon_{{\rm xc},i}(n({\bf r})) = \epsilon_{{\rm x},i}(n({\bf r... ...t\{ (1+x_i^3)\log{(1+x_i^{-1})} +\frac{1}{2} x_i - x_i^2 -\frac{1}{3} \right\}$$

où $i \in \{p,f\}$ et les autres termes sont

$$\epsilon_{{\rm x},p} = -\frac{0.916}{r_s} \qquad,\qquad \epsilon_{{\rm x},f} = 2^{1/3}\epsilon_{{\rm x},p}$$

$$x_i = \frac{r_s}{r_i} \qquad,\qquad r_s = \left(\frac{3}{4\pi n({\bf r})}\right)^{1/3}$$

$$c_p = 0.066\,Ry \quad,\quad c_f = 0.0406\,Ry \quad,\quad r_p = 11.4\, \,{\rm a}_0 \quad,\quad r_f = 15.9\, \,{\rm a}_0 \quad.$$

Notons qu'avec cette fonctionnelle, le potentiel d'échange-corrélation dans le cas non polarisé en spin vaut :

$$v_{xc}=-1,222/r_s({\bf r})-0,0666\log (1+\frac{11,4}{r_s({\bf r})})$$

On peut reconnaître dans le premier terme l'approximation de type Slater pour l'échange.

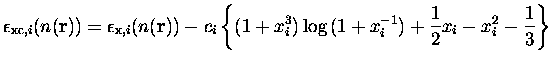
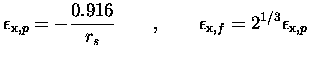
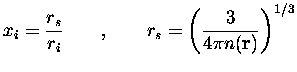
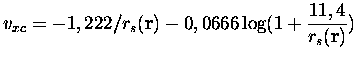
Nous aurions pu utiliser des fonctionnelles plus modernes, en particulier non-locales (développement en gradient GGA par exemple), mais dans un souci de cohérence avec les calculs de référence dont nous disposions sur les agrégats de sodium nous avons préféré garder cette fonctionnelle qui a fait ses preuves depuis le premier article théorique publié sur la question [32]. Il est à noter que pour certains métaux, comme l'aluminium, où la densité électronique varie beaucoup plus brutalement que dans le cas du sodium, un tel traitement serait inadapté.