


Next: LDA-LSD
Up: Fonctionnelle de la densité
Previous: État fondamental
Table des matières
Séparons arbitrairement la fonctionnelle ![$ E[n]$](img348.gif) de la façon suivante :
de la façon suivante :
![$\displaystyle E[n]=T_{\mbox{\scriptsize0}}[n]+ \int \!d{\bf r} \, n({\bf r}) \l...
... ext}}({\bf r})+ \frac{1}{2}\Phi({\bf r}) \right] +E_{\mbox{\scriptsize xc}}[n]$](img349.gif) |
(25) |
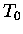 est l'énergie cinétique qu'un système
d'électrons de densité
est l'énergie cinétique qu'un système
d'électrons de densité 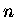 aurait s'il n'y avait pas d'interaction,
aurait s'il n'y avait pas d'interaction,
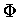 est le potentiel coulombien classique (obéissant à l'équation de
Poisson
est le potentiel coulombien classique (obéissant à l'équation de
Poisson
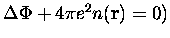 et
et
![$ E_{\mbox{\scriptsize xc}}[n]$](img352.gif) , la partie restante, est ce que nous
appellerons l'énergie d'échange-corrélation. Il faut remarquer que,
contrairement à l'approche de Thomas-Fermi,
, la partie restante, est ce que nous
appellerons l'énergie d'échange-corrélation. Il faut remarquer que,
contrairement à l'approche de Thomas-Fermi,
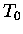 est exact, ce qui améliore grandement les résultats car les effets de
fermeture de couche interviennent explicitement.
est exact, ce qui améliore grandement les résultats car les effets de
fermeture de couche interviennent explicitement.
Le principe variationnel appliqué à A.5 donne
où 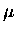 est le multiplicateur de Lagrange associé à la contrainte de
normalisation de la densité. Si nous comparons cette équation à
l'équation correspondante pour un système d'électrons sans
interactions mutuelles soumis à un potentiel
extérieur
est le multiplicateur de Lagrange associé à la contrainte de
normalisation de la densité. Si nous comparons cette équation à
l'équation correspondante pour un système d'électrons sans
interactions mutuelles soumis à un potentiel
extérieur
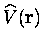 ,
,
on voit que les deux problèmes sont identiques, pourvu que
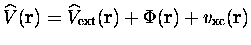 |
(28) |
où l'on a posé
![$ v_{\mbox{\scriptsize xc}}({\bf r})
=
\frac{\displaystyle \delta E_{\mbox{\scriptsize xc}}[n] }
{ \displaystyle \delta n({\bf r})}
$](img358.gif) .
.
La solution de A.7 est obtenue immédiatement : puisque le
système est sans interaction, la fonction d'onde multiélectronique est
simplement un produit antisymétrisé de fonctions d'onde
monoélectroniques 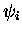 obéissant à l'ensemble d'équations de
Schrödinger :
obéissant à l'ensemble d'équations de
Schrödinger :
![$\displaystyle \left[- \frac{\hbar^2}{2m_{el}} \Delta + \widehat{V}({\bf r}) \right] \psi_i({\bf r}) = \epsilon_i \psi_i({\bf r})$](img51.gif) |
(29) |
d'où
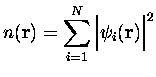 |
(30) |
et dans le cas avec interaction on obtient des équations à un corps
appelées équations de Kohn-Sham, qui sont couplées et non-linéaires car
le potentiel
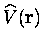 y dépend de la densité. Ces
équations peuvent néanmoins être résolues par une procédure
autocohérente que nous décrirons page
y dépend de la densité. Ces
équations peuvent néanmoins être résolues par une procédure
autocohérente que nous décrirons page ![[*]](cross_ref_motif.gif) . Il est à noter que
les équations obtenues sont de la forme de Hartree ; il n'y a pas
d'opérateur non-local du type Fock qui intervienne, ce qui simplifie
les calculs. La seule approximation porte sur le terme
d'échange-corrélation
. Il est à noter que
les équations obtenues sont de la forme de Hartree ; il n'y a pas
d'opérateur non-local du type Fock qui intervienne, ce qui simplifie
les calculs. La seule approximation porte sur le terme
d'échange-corrélation
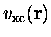 qui n'est pas connu
exactement. Nous recourrons à l'approximation
locale (LDA) que nous allons présenter.
qui n'est pas connu
exactement. Nous recourrons à l'approximation
locale (LDA) que nous allons présenter.



Next: LDA-LSD
Up: Fonctionnelle de la densité
Previous: État fondamental
Table des matières
Florent Calvayrac
1999-05-05
![]() de la façon suivante :
de la façon suivante :
![$\displaystyle \frac{\delta E[n]}{\delta n({\bf r})}$](img353.gif)
![$\displaystyle \frac{\delta T_{\mbox{\scriptsize0}}[n]}{\delta n({\bf r})}
+
\wi...
...
\Phi({\bf r})
+
\frac{\delta E_{\mbox{\scriptsize xc}}[n] }{\delta n({\bf r})}$](img354.gif)
![]() est le multiplicateur de Lagrange associé à la contrainte de
normalisation de la densité. Si nous comparons cette équation à
l'équation correspondante pour un système d'électrons sans
interactions mutuelles soumis à un potentiel
extérieur
est le multiplicateur de Lagrange associé à la contrainte de
normalisation de la densité. Si nous comparons cette équation à
l'équation correspondante pour un système d'électrons sans
interactions mutuelles soumis à un potentiel
extérieur
![]() ,
,
![$ v_{\mbox{\scriptsize xc}}({\bf r})
=
\frac{\displaystyle \delta E_{\mbox{\scriptsize xc}}[n] }
{ \displaystyle \delta n({\bf r})}
$](img358.gif) .
.
![]() obéissant à l'ensemble d'équations de
Schrödinger :
obéissant à l'ensemble d'équations de
Schrödinger :
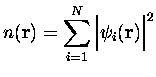
![[*]](cross_ref_motif.gif) . Il est à noter que
les équations obtenues sont de la forme de Hartree ; il n'y a pas
d'opérateur non-local du type Fock qui intervienne, ce qui simplifie
les calculs. La seule approximation porte sur le terme
d'échange-corrélation
. Il est à noter que
les équations obtenues sont de la forme de Hartree ; il n'y a pas
d'opérateur non-local du type Fock qui intervienne, ce qui simplifie
les calculs. La seule approximation porte sur le terme
d'échange-corrélation