Lorsque nous avons présenté la théorie de la fonctionnelle statique ou
dépendant du temps, il avait toujours été supposé que le
mouvement des noyaux atomiques pouvait être négligé.
Dans les exemples qui nous intéressent, à savoir les petits agrégats de
sodium en particulier, ce mouvement doit être pris en compte lorsqu'on
s'intéresse à des phénomènes sur une échelle de temps supérieure à une
centaine de femtosecondes, surtout, lorsque comme ici, on
considère des processus déposant une grande quantité d'énergie dans le
nuage électronique. Une partie de cette énergie pourra alors se
transférer aux degrés de liberté ioniques (en assimilant électrons de
c![]() ur et noyau en un ion) de façon à déclencher leur
mouvement. Il faut donc écrire des équations du mouvement pour ces ions.
Nous allons résumer pour ce faire les discussions de [31].
ur et noyau en un ion) de façon à déclencher leur
mouvement. Il faut donc écrire des équations du mouvement pour ces ions.
Nous allons résumer pour ce faire les discussions de [31].
Considérons d'abord de façon générale le système sous la forme de ![]() électrons et de
électrons et de ![]() noyaux, de charge
noyaux, de charge ![]() et de masse
et de masse ![]() ,
,
![]() . Soit
. Soit
![]() le vecteur position du
le vecteur position du
![]() -ième noyau de l'espèce
-ième noyau de l'espèce ![]() . L'équation de Schrödinger du
système s'écrit alors
. L'équation de Schrödinger du
système s'écrit alors
![$\displaystyle i\hbar
\frac{\partial}{\partial t}
\Psi
=
\left[
\widehat{H}_e({...
...n}({\bf r}_1,\ldots,{\bf r}_N,\left\{{\bf R}_{A\alpha}\right\}t)
\right]
\Psi
$](img400.gif)
![]() étant la fonction d'onde exacte du système complet:
étant la fonction d'onde exacte du système complet:
Le Hamiltonien électronique est toujours :
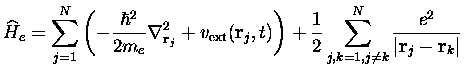
le Hamiltonien nucléaire
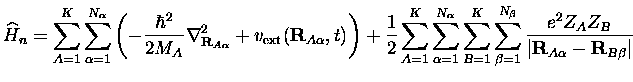
les indices ![]() et
et ![]() étant naturellement différents.
L'interaction électron-noyau, elle, s'écrit simplement
étant naturellement différents.
L'interaction électron-noyau, elle, s'écrit simplement
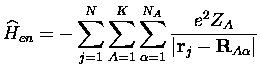
En analogie avec les théorèmes de la fonctionnelle de la densité
dépendant du temps pour les électrons seuls, on peut établir à partir
d'un état initial ![]() une relation biunivoque (du type du théorème
de Hohenberg-Kohn) entre l'ensemble
des potentiels extérieurs et l'ensemble des densités électroniques et
nucléaires (pour chaque espèce), à un instant donné.
une relation biunivoque (du type du théorème
de Hohenberg-Kohn) entre l'ensemble
des potentiels extérieurs et l'ensemble des densités électroniques et
nucléaires (pour chaque espèce), à un instant donné.
De là découle un ensemble d'équations de Kohn-Sham dépendant du temps pour les noyaux et les électrons.
\right)
\phi_j({\bf r},t) $](img407.gif)
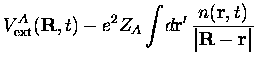 |
|||
$](img415.gif) |
Les potentiels d'échange-corrélation pour les noyaux sont eux aussi des dérivées fonctionnelles de l'action, comme dans le cas avec noyaux fixes. Dans les systèmes moléculaires que nous considérons, l'échange entre noyaux identiques est faible car aux séparations nucléaires usuelles le recouvrement des fonctions d'onde nucléaires est peu important. Cependant, il faudrait en principe appliquer une procédure du type SIC (Self-Interaction Correction) pour annuler les termes d'auto-interaction contenus dans les termes de type Hartree de l'équation précédente.
Même avec ces simplifications, la résolution de cet ensemble d'équations reste très lourde. On peut cependant [31] reprendre la discussion précédente en ne considérant que les électrons de valence et en remplaçant le potentiel coulombien créé par les noyaux par un pseudopotentiel pertinent. C'est ce que nous allons faire dans toute la suite, employant les pseudopotentiels que nous avons présentés ; de plus, nous allons encore plus simplifier le problème en traitant le mouvement des noyaux en mécanique classique. Nous continuerons cependant à utiliser le terme coulombien dans les équations au lieu de pseudopotentiels, dans un souci de simplicité.
En appliquant le théorème d'Ehrenfest à l'équation C.1 de Kohn-Sham pour les noyaux, la trajectoire classique
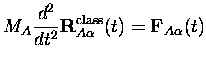
Remarquons au passage que puisqu'en principe les
équations de Kohn-Sham dépendant du temps donnent
les densités exactes, l'équation C.2 donne la trajectoire exacte
classique s'il n'y a qu'un noyau de l'espèce ![]() . Sinon, on a un
ensemble de particules indiscernables et les trajectoires de noyaux
individuels ne peuvent pas être définies classiquement
; seule la trajectoire du centre de masse a un sens.
On utilisera toujours cependant
l'équation C.2 afin d'imposer une définition des
trajectoires classiques des noyaux.
. Sinon, on a un
ensemble de particules indiscernables et les trajectoires de noyaux
individuels ne peuvent pas être définies classiquement
; seule la trajectoire du centre de masse a un sens.
On utilisera toujours cependant
l'équation C.2 afin d'imposer une définition des
trajectoires classiques des noyaux.
Avec l'approximation SIC dont nous parlions plus haut, l'expression de la
force
![]() devient
devient
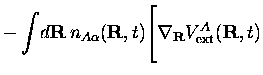 |
|||
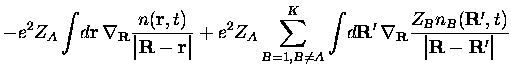 |
|||
![$\displaystyle +
e^2Z_A\sum_{\beta=1,\beta \neq \alpha}^{N_A}\int\!d{\bf R}'\,
\...
...}}
\frac{Z_An_{A\beta}({\bf R}',t)}
{\big\vert{\bf R}-{\bf R}'\big\vert}
\Bigg]$](img423.gif) |
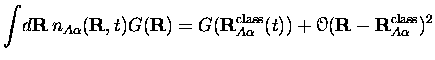
Négliger les termes d'ordre supérieur revient à écrire
![]() .
Les équations du mouvement se réduisent alors à
.
Les équations du mouvement se réduisent alors à
Ces équations sont donc à résoudre en même temps que les équations de Kohn-Sham dépendant du temps pour les électrons, auxquelles elles sont couplées. Malgré les nombreuses hypothèses et simplifications qui ont été faites, le traitement ici présenté ne fait pas appel à l'approximation de Born-Oppenheimer : on résout des équations dépendant du temps pour les électrons et non pas des équations de Kohn-Sham statiques. D'autre part, l'orthogonalité des fonctions d'onde électroniques au cours du temps n'a pas besoin d'être imposée comme dans le schéma de Car-Parinello.