Modifications de la longueur d'un parcours rectiligne par de petits déplacements des extrémités
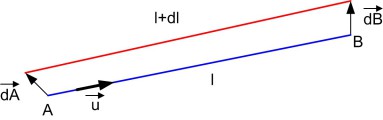
La longueur \(l = AB\) peut s'exprimer par le module du vecteur \(\overrightarrow{AB}\) :
\(l = \overrightarrow{u} \cdot \overrightarrow{AB}\)
(Produit scalaire)
\(\overrightarrow{u}\) est le vecteur unitaire dans la direction \(AB\). Pour de petits déplacements de \(A\) et de \(B\) notés \(\overrightarrow{dA}\) et \(\overrightarrow{dB}\), nous avons
\(d(\overrightarrow{AB}) = \overrightarrow{dB} - \overrightarrow{dA}\)
puis
\(dl = \overrightarrow{du} \cdot \overrightarrow{AB} + \overrightarrow{u} \cdot d(\overrightarrow{AB})\)
\(\overrightarrow{du} \mbox{ est perpendiculaire à } \overrightarrow{AB} \mbox{ donc } \overrightarrow{du} \cdot \overrightarrow{AB} = 0 \mbox{ , on en déduit : }\)
\(dl = \overrightarrow{u} \cdot (\overrightarrow{dB} - \overrightarrow{dA})\)
Si l'indice du milieu est n et \(L = nAB\) le chemin optique \((AB)\), la variation de chemin optique \(dL\) est :
\(dL = n \overrightarrow{u} \cdot (\overrightarrow{dB} - \overrightarrow{dA}) \mbox{ (3)}\)