Lois de la réfraction
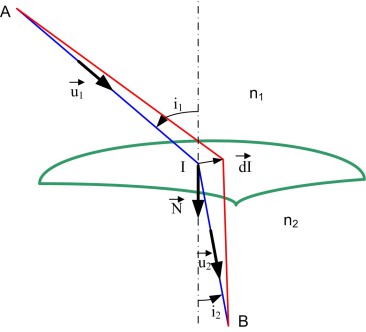
Considérons une surface \(S\) de l'espace, séparant deux milieux d'indices respectifs \(n_{1}\) et \(n_{2}\) contenant respectivement les point \(A\) et \(B\). Le trajet effectivement suivi par la lumière pour aller de \(A\) à \(B\) passe par le point \(I\) sur la surface.
\(AI\) est le rayon incident, \(IB\) est le rayon réfracté.
\(L = n_{1} \cdot AI + n_{2} \cdot IB\) est le chemin optique \((AIB)\).
Un petit déplacement \(dI\) de \(I\) provoque une variation \(dL\) telle que \(dL/dI = 0\) en vertu du principe de Fermat. L'expression (3) appliquée aux parcours \(AI\) et \(IB\) donne :
\(dL_{AI} = n_{1} \overrightarrow{u_{1}} \cdot (\overrightarrow{dI} - \overrightarrow{dA}) = n_{1} \overrightarrow{u_{1}} \cdot \overrightarrow{dI}\)
de même
\(dL_{IB} = n_{2} \overrightarrow{u_{2}} \cdot (\overrightarrow{dB} - \overrightarrow{dI}) = - n_{2} \overrightarrow{u_{2}} \cdot \overrightarrow{dI}\)
Puisque \(\overrightarrow{dA} = \overrightarrow{dB} = 0\), finalement :
\(dL_{AB} = - ( n_{2} \overrightarrow{u_{2}} - n_{1} \overrightarrow{u_{1}} ) \cdot \overrightarrow{dI}\)
Si \(\overrightarrow{N}\) est le vecteur unitaire dans la direction de la normale, \(\overrightarrow{V}\) celui dans la direction \(\overrightarrow{dI}\).
\(\overrightarrow{dI} = \overrightarrow{V} \cdot dI\) soit :
\(dL_{AB} = - ( n_{2} \overrightarrow{u_{2}} - n_{1} \overrightarrow{u_{1}} ) \cdot \overrightarrow{V} \cdot dI\)
Le principe de Fermat imposant, pour un trajet effectivement suivi par la lumière, \(dL/dI = 0\) pour tout \(\overrightarrow{dI}\), \(( n_{2} \overrightarrow{u_{2}} - n_{1} \overrightarrow{u_{1}} )\) et \(\overrightarrow{V}\) sont perpendiculaires donc \(( n_{2} \overrightarrow{u_{2}} - n_{1} \overrightarrow{u_{1}} )\) et \(\overrightarrow{N}\) sont parallèles.
\(( n_{2} \overrightarrow{u_{2}} - n_{1} \overrightarrow{u_{1}} ) = k \overrightarrow{N}\) montre que \(\overrightarrow{u_{1}}, \overrightarrow{u_{2}}\) et \(\overrightarrow{N}\) appartiennent à un même plan \(P\).
P est le plan d'incidence, il contient le rayon incident, le rayon réfracté et la normale à la surface en \(I\), \(i_{1}\) et \(i_{2}\) sont, dans ce plan, les angles entre les rayons incidents et réfractés par rapport à la normale. On en déduit la relation de réfraction vectorielle :
\(( n_{2} \overrightarrow{u_{2}} - n_{1} \overrightarrow{u_{1}} ) = (n_{2} cosi_{2} - n_{1} cosi_{1} ) \cdot \overrightarrow{N} \mbox{ (4)}\)
Et, par projection dans le plan de la surface :
\(n_{1} \cdot sini_{1} = n_{2} \cdot sini_{2} \mbox{ (5)}\)
Les lois de Descartes se déduisent des relations précédentes:
Loi 1 : Le rayon réfracté est dans le plan d'incidence
Loi 3 : Les angles \(i_{1}\) et \(i_{2}\) des rayons incidents et réfléchis sont tels que \(n_{1} \cdot sini_{1} = n_{2} \cdot sini_{2}\)
La loi 2 concerne les surfaces réfléchissantes, pour lesquelles \(i_{1} = - i_{2}\) . On verra par la suite que les formules des surfaces réfractantes s'appliquent aux surfaces réfléchissantes en prenant : \(n_{2}=-n_{1}\).
Réfraction
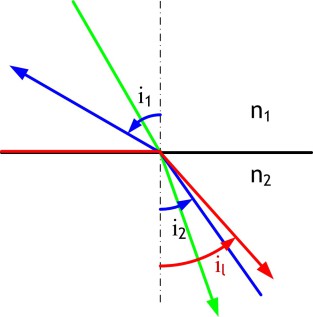
Considérons deux milieux d'indices \(n_{1}\) et \(n_{2}\), la troisième loi de Descartes nous donne la relation entre les angles d'incidence et de réfraction dans les deux milieux :
\(n_{1} \cdot sini_{1} = n_{2} \cdot sini_{2} \mbox{ (5)}\)
Cette relation est parfaitement symétrique, en accord avec le principe du retour inverse de la lumière. Un rayon venant du deuxième milieu faisant l'angle \(i_{2}\) avec la normale fera, après réfraction par la surface, un angle \(i_{1}\) dans le premier milieu satisfaisant à la relation (5).
Angle limite
Angle limite
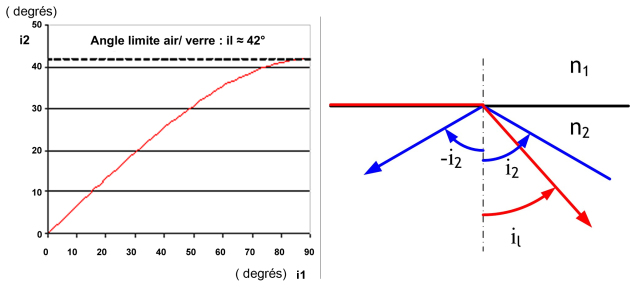
Pour \(i_{l} = 90^{ \circ}\), incidence rasante, le rayon réfracté fait, avec la normale l'angle \(i_{2}\) tel que : \(sini_{2}=n_{1}/n_{2}\).
\(i_{2}\) est alors appelé l'angle limite \(i_{l}\)
\(i_{l} = \arcsin (n_{1} / n_{2}) \mbox{ (6)}\)
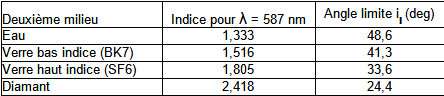
Tout rayon provenant du deuxième milieu dont l'angle d'incidence \(i_{2}\) est supérieur à \(i_{l}\) subit une réflexion totale. Si le premier milieu est l'air \((n_{1}=1)\), le tableau ci-dessous donne quelques valeurs de \(i_{l}\) :
Réflexion totale dans une fibre optique multimodale :
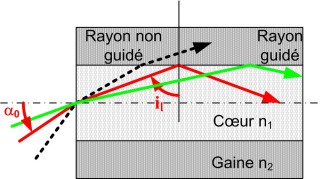
L'indice du cœur est \(n_{1}\), l'indice de la gaine est \(n_{2}< n_{1}\).
Un rayon lumineux qui a une incidence supérieure à \(i_{1}\) sur l'interface cœur-gaine se réfléchit totalement, il est guidé.
Son incidence à l'entrée de la fibre est inférieure à \(\alpha _{0}\).
\(\alpha _{0}\) est le demi-angle d'ouverture de la fibre. L'ouverture numérique de la fibre est :
\(NA = \sin (\alpha _{0}) = \sqrt{n_{1}^{2} - n_{2}^{2}}\)