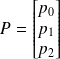Régression linéaires et moindres carrés en traitement des images
Fondamental : Régression linéaire à dans le plan
Soient m observations
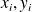 . On veut trouver une relation linéaire par rapport à
. On veut trouver une relation linéaire par rapport à
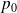 et
et
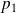 telle que :
telle que :
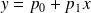
L'équation précédente peut se mettre, pour l'ensemble des données x_i,y_i, sous forme matricielle :
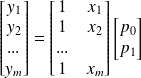
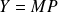
la matrice M est rectangulaire donc non inversible. Pour trouver p résoudre ce système, on multiplie chaque membre par la transposé de M :
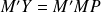
M'M est une matrice carrée donc inversible. L'expression de p est alors :
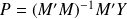
La matrice
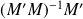 est la pseudoinverse de la matrice rectangulaire M
est la pseudoinverse de la matrice rectangulaire M
Exemple : Recherche d'une cubique passant par 3 points
Notre modèle
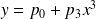
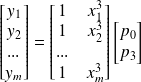
Nos mesures sont, sous la forme
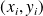 :
:
(1,5) (2 ,8) (3,7)
La matrice M est donc
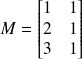
Avec Scilab la pseudoinverse est
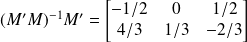
Remarque : Ordre des paramètres dans le modèle
Au lieu de
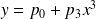 , on peut écrire
, on peut écrire
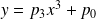 on aura alors :
on aura alors :
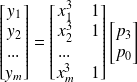
Les calculs seront identiques , mais le résultat dans l'ordre inverse : il faut simplement se souvenir de l'ordre.
Fondamental : Régression linéaire dans un volume
Soient m observations
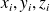 . On veut trouver une relation linéaire par rapport à
. On veut trouver une relation linéaire par rapport à
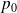 ,
,
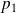 et
et
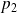 telle que :
telle que :
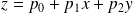
Z=MP avec
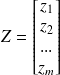 et
et
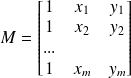 et enfin
et enfin