Représentation des fonctions d'onde et discrétisation

Nous avons choisi de représenter les fonctions d'onde électroniques sur une grille spatiale à deux dimensions, lorsque nous supposons une symétrie axiale pour la distribution électronique, ou à trois dimensions lorsque toutes les restrictions de symétrie ont été levées.

Ce choix a été inspiré par les travaux de Reinhard et de ses collaborateurs sur les propriétés statiques ou linéarisées des agrégats de sodium, eux-mêmes issus des travaux précédents de ce groupe en physique nucléaire, qui comportaient des versions dépendant du temps formellement équivalentes au problème que nous voulons résoudre [49].

Ces travaux utilisaient les méthodes Hartree-Fock dépendant du temps, appliquées en physique nucléaire depuis le début des années 1970, pour modéliser la fusion des noyaux de masse intermédiaire [50]. Dans toutes ces études, les fonctions d'onde des nucléons se sont avérées pouvoir être bien représentées sur des grilles régulières en espace, qui sont pratiques à manipuler et très souples d'usage, comme il est démontré dans [51].

Par ailleurs, les nombreuses similarités entre agrégats métalliques, en particulier de sodium, et noyaux atomiques ne s'arrêtent pas à l'existence de nombres magiques : le potentiel de Kohn-Sham auquel sont soumis les électrons de valence dans un agrégat de sodium présente une allure tout à fait semblable à celle du potentiel effectif de Woods-Saxon subi par les nucléons dans un noyau de taille intermédiaire. Bien que les échelles de distance et d'énergie ne soient pas du tout les mêmes, il est naturel d'appliquer aux électrons de valence des agrégats métalliques des techniques qui ont fait leurs preuves en physique nucléaire, donc de discrétiser les fonctions d'onde sur une grille régulière en espace.

De plus, il est frappant de constater la similarité des équations de Kohn-Sham et de celles qui sont appelées << de Hartree-Fock >> en physique nucléaire, c'est à dire des équations de Hartree à un corps avec un potentiel effectif incluant l'échange (forces de Skyrme). Les méthodes numériques et même les programmes peuvent donc être repris des travaux de physique nucléaire.

En physique atomique ou moléculaire, on est cependant plus habitué à projeter les fonctions d'onde dans différentes bases bien adaptées aux problèmes, par exemple des bases de gaussiennes, mais ces méthodes, très avantageuses, car adaptées à la forme des orbitales atomiques et à leur symétrie, transforment leurs avantages en obstacles lorsqu'il s'agit d'exciter les fonctions d'onde de façon arbitraire, ou de calculer l'évolution simultanée des positions des noyaux atomiques et des électrons. Les physiciens du solide travaillent souvent sur des bases d'ondes planes, mais les agrégats métalliques sont des systèmes localisés et finis, donc il vaut mieux travailler en espace direct.

Dans le cas des agrégats, il est plus avantageux de discrétiser les fonctions d'onde sur une grille régulière en espace. En dehors de Reinhard et de ses collaborateurs, plusieurs auteurs on fait de même. Dans le cas des agrégats métalliques, Landman et ses collaborateurs ont ainsi simulé dans [52] la fission de petits agrégats de sodium multichargés en résolvant une dynamique Born-Oppenheimer pour les ions, les fonctions d'onde électroniques étant représentés sur une grille régulière en trois dimensions d'espace direct. Yabana et Bertsch ont calculé la dynamique non-linéarisée des électrons de valence dans des agrégats de lithium ou de carbone également sur une grille régulière dans [53]. Parmi les travaux dont nous avons eu connaissance en physique moléculaire, on peut citer les travaux de [54] de dynamique moléculaire dans des molécules pour obtenir des spectres vibrationnels, toujours avec usage de grilles régulières.

Dans les études que nous avons effectuées au début de cette thèse, nous avons donc repris un programme de physique nucléaire restreint à la symétrie axiale où chaque fonction d'onde intervenant dans les équations à un corps est représentée aux points

$$r_i=(i-1/2)\Delta r \;\;\;\; 1\leq i \leq N_r$$

$$z_j=(j-1)\Delta z \;\;\;\; 1\leq j \leq N_z$$

Ensuite, nous avons écrit à partir d'un programme destiné à étudier les propriétés de l'état fondamental des agrégats métalliques dans le modèle du << jellium >> déformé à trois dimensions, un programme avec dynamique électronique sans aucune restriction de symétrie, où les fonctions d'onde sont représentées sur une grille tridimensionnelle :

$\parbox{12cm}{ \begin{displaymath}x_i=(i-N_x)\Delta x \;\;\;\; 1\leq... ...in{displaymath}z_k=(k-N_z)\Delta z \;\;\;\; 1\leq k \leq 2N_z\end{displaymath}}$

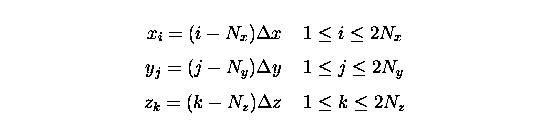
Dans le cas typique que nous avons étudié, Na$_9^+$, il y a trois fonctions d'onde à représenter sur le réseau si on suppose la symétrie axiale et la dégénérescence en spin (une fonction << 1s >> et deux fonctions << 2s >> et << 2p >>), et huit dans le cas à trois dimensions sans restriction de spin. Puisque les pseudopotentiels que nous utilisons étaient manipulés via leurs pseudodensités gaussiennes, et que ces gaussiennes sont numériquement représentées de manière optimale en fonction de conditions sur la grille dont nous discutons dans l'annexe E, il s'avère nécessaire de prendre un espacement de grille adapté, de 0.8 a$_0$ par exemple dans le cas des pseudopotentiels de [38]. Dans le cas du << jellium >>, il faut prendre un espacement similaire car il correspond à la largeur de surface du << jellium >> adouci.

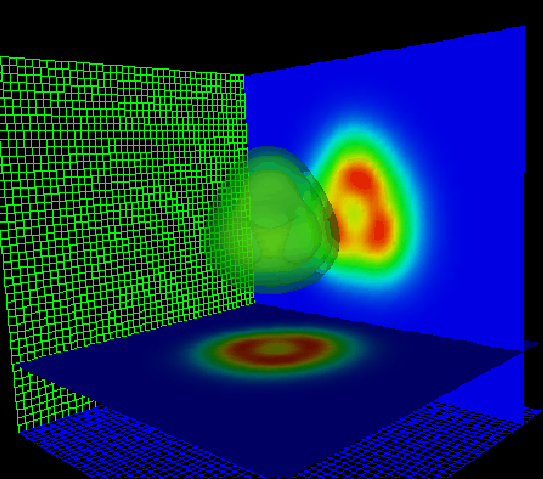
Pour la taille des boîtes, le problème change suivant la nature des conditions aux limites employées durant la propagation. En effet, dans le cas de conditions aux limites réfléchissantes, la partie du nuage électronique de l'agrégat qui est émise lors du processus d'excitation revient perturber la dynamique après une réflexion sur les bords de la boîte. Il faut donc employer des conditions aux limites absorbantes, à la limite périodiques (la fréquence du retour est divisée par deux), ou augmenter la taille de la boîte. Pour cette raison, nous avons pu prendre des boîtes de 48 points dans le cas tridimensionnel, où nous avions le choix des conditions aux limites, alors que dans le cas à symétrie axiale, où un algorithme de propagation ayant implicitement des conditions aux limites réfléchissantes (méthode de Crank-Nicholson dont nous allons parler dans la suite) était employé, nous avons dû prendre, à moins d'introduire des conditions aux limites absorbantes, des boîtes d'une centaine de points dans la direction d'excitation, et d'une trentaine dans la direction transverse.

Figure: Densité électronique pour l'agrégat Na$_9^+$ dans la configuration 144(représentée figure III.1 page ) , isomère à symétrie axiale. On montre ici différentes isosurfaces pour la densité électronique, deux coupes par le milieu de l'agrégat translatées pour une meilleure visibilité, ainsi que le fond de la grille $48^3$ en arrière-plan