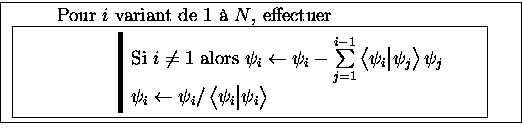


Next: Calcul du Hamiltonien
Up: Parallélisation
Previous: Itérations dynamiques
Table des matières
Les schémas itératifs pour calculer l'état fondamental du système, tels
qu'ils ont été présentés page ![[*]](cross_ref_motif.gif) , sont pourtant très similaires
aux schémas dynamiques présentés page
, sont pourtant très similaires
aux schémas dynamiques présentés page ![[*]](cross_ref_motif.gif) , même moins exigeants, puisque
les fonctions d'onde peuvent y être prises réelles, alors que la
dynamique exige par essence des fonctions d'onde complexes, mais ils
présentent la grave difficulté de demander une orthonormalisation des
fonctions d'onde à chaque pas. Dans notre approche consistant à charger
chaque processeur d'une fonction d'onde, cela implique donc bien plus de
communications que dans le cas dynamique.
, même moins exigeants, puisque
les fonctions d'onde peuvent y être prises réelles, alors que la
dynamique exige par essence des fonctions d'onde complexes, mais ils
présentent la grave difficulté de demander une orthonormalisation des
fonctions d'onde à chaque pas. Dans notre approche consistant à charger
chaque processeur d'une fonction d'onde, cela implique donc bien plus de
communications que dans le cas dynamique.
Puisque nous avons choisi le procédé de Schmidt(POS) pour réaliser cette
orthonormalisation, c'est elle que nous avons parallélisée, en chargeant
chaque processeur d'orthogonaliser << sa >> fonction d'onde avec toutes
celles de rang inférieur au sien.
Rappelons en effet le mécanisme du POS, pour un ensemble de 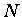 fonctions d'onde
fonctions d'onde 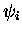 de même spin
de même spin![[*]](foot_motif.gif) . La méthode peut s'exprimer de la façon suivante :
. La méthode peut s'exprimer de la façon suivante :
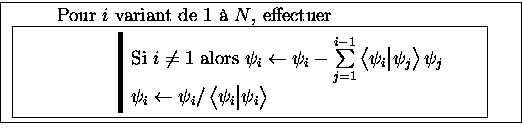
Il faut donc qu'un processeur d'indice 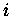 reçoive tous les
reçoive tous les
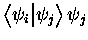 des processeurs de
des processeurs de 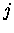 strictement inférieur.
strictement inférieur.
Nous avons d'abord programmé le POS à l'aide des extensions CRAFT au
Fortran, où les communications sont implicites, ce qui nous a permis
d'avoir rapidement une implantation de l'algorithme certainement pas
optimale en ce qui concerne la rapidité, mais qui nous a progressivement
permis de transformer le programme jusqu'à ce qu'il ne fasse plus appel
qu'aux bibliothèques de passage de messages explicites(PVM,SHMEM puis
MPI). Ces bibliothèques, très similaires d'usage, permettent de
meilleures performances puisqu'avec elles on peut contrôler directement
les communications ; de plus, elles existent sur différentes plateformes
(CRAY comme IBM) ce qui n'est pas le cas de CRAFT, limité au CRAY T3D.
Dans le modèle SPMD (Single Program Multiple Data)
chaque processeur (PE) exécute alors l'algorithme suivant :
(pour le PE d'indice 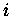 )
)

On voit que cet algorithme ne bénéficie de la parallélisation que par le
fait que des fonctions d'onde de spin différents peuvent être
orthogonalisées simultanément, et par le fait que l'opérateur de
gradient amorti est appliqué en même temps par tous les processeurs. Il
faut cependant remarquer que le processus d'orthonormalisation est par
essence un mélange de toutes les fonctions d'onde ; d'autre part,
l'avantage d'avoir parallélisé le pas de temps statique est à trouver
dans la flexibilité qu'on gagne à avoir un programme parallèle
entièrement autonome, capable de calculer la condition initiale comme la
propagation dynamique. On peut bénéficier alors de la mémoire énorme
disponible sur les calculateurs tels que les T3D/T3E ou SP2 pour
étudier des systèmes nécessitant de vastes grilles, ou possédant un
grand nombre de fonctions d'onde.



Next: Calcul du Hamiltonien
Up: Parallélisation
Previous: Itérations dynamiques
Table des matières
Florent Calvayrac
1999-05-05
![[*]](cross_ref_motif.gif) , sont pourtant très similaires
aux schémas dynamiques présentés page
, sont pourtant très similaires
aux schémas dynamiques présentés page ![[*]](cross_ref_motif.gif) , même moins exigeants, puisque
les fonctions d'onde peuvent y être prises réelles, alors que la
dynamique exige par essence des fonctions d'onde complexes, mais ils
présentent la grave difficulté de demander une orthonormalisation des
fonctions d'onde à chaque pas. Dans notre approche consistant à charger
chaque processeur d'une fonction d'onde, cela implique donc bien plus de
communications que dans le cas dynamique.
, même moins exigeants, puisque
les fonctions d'onde peuvent y être prises réelles, alors que la
dynamique exige par essence des fonctions d'onde complexes, mais ils
présentent la grave difficulté de demander une orthonormalisation des
fonctions d'onde à chaque pas. Dans notre approche consistant à charger
chaque processeur d'une fonction d'onde, cela implique donc bien plus de
communications que dans le cas dynamique.
![[*]](foot_motif.gif)